18. Ряд Тейлора функции комплексной переменной. Формулы разложения в ряд Маклорена основных элементарных функций.

19. Нули аналитической функции.

Пусть функция F(z) является аналитической в точке Z₀

Точка называется нулем функции , если ее значение в этой точке равно нулю, т.е. .

В разложении функции в ряд Тейлора в окрестности нуля той функции отсутствует свободный член: . Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности до n-й степени, т.е. разложение имеет вид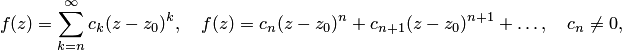

то точка называется нулем порядка функции . Нуль первого порядка называется простым нулем.

Правую часть равенства (3.20) можно записать в виде произведения:

, или (3.20) ,

где второй множитель можно рассматривать как степенной ряд, сходящийся в точке , поэтому его сумма — функция, аналитическая в точке ; обозначим ее . Таким образом, из (3.20) получаем представление функции в виде

(3.21)

Кроме того, используя формулу коэффициентов ряда Тейлора , находим, что для нуля порядка функции в точке справедливо условие

(3.22)

т.е. порядок нуля функции определяется порядком первой отличной от нуля в этой точке производной.

Пусть функция задана в виде произведения и точка является нулем порядка для и нулем порядка для . Тогда, используя условие (3.21) для этих функций, можно записать

или

(3.23)

Это означает, что порядок нуля в точке функции, полученной в результате перемножения аналитических функций, равен сумме порядков нуля в этой точке функций-сомножителей.

Утверждение 1

1. Точка является нулем функции , если ; нулем порядка -если для коэффициентов ряда Тейлора ее разложения по степеням справедливы равенства

2. Следующие условия являются необходимыми и достаточными условиями пуля порядка п функции в точке

а) условие (3.22): ; б) представление функции в виде произведения (3.21): .

Замечания 1

1. Если функция не определена в точке , но , то после доопределения функции в точке , точку тоже называют нулем функции.

2. Пусть представлена в виде отношения аналитических в точке функций и точка является нулем порядка для числителя и нулем порядка — для знаменателя. При условии , доопределив функцию , выше, получим, — нуль функции .

Используя условие (3.21) для функций и , получаем равенство , или . Здесь — аналитическая в точке , так как и — аналитические в этой точке и . Кроме того, , так как . Поэтому для функции точка является нулем порядка (см. (3.21)). Порядок нуля частного равен разности — из порядка нуля числителя вычитается порядок нуля знаменателя.

20. Ряд Лорана. Главная т правильная части ряда Лорана. Формулы для коэффициентов. Область сходимости.

21. Классификация особых точек по разложению функции в ряд Лорана.

Особой точкой называется функция f(z) , точка в которой не является аналитической.

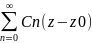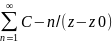Z = z ₀-особая точка f(z), особая точка называется изолированной, если в некоторой окресности её функции f(z ) не имеет других особых точек. Если R>0, то 0<(z-z₀)<R будет аналитической и будет разлагаться в ряд лорана f(z)= ⁿ+ ⁿ. Ряд Лорана не содержит главной части нет членов с отрицательными показателями, z₀-устранимая точка функции f(z). Главные части ряда Лорана конечное число членов, в этом случае z₀-называется полюсом функции. Главные части Лорана содержат бесконечное множество членов, тогда z₀-называется существенной точкой фуекции.