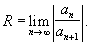16. Определения и свойства абсолютно сходящихся рядов в комплексной области.

Ряд называется абсолютно сходящимся, если сходится ряд , составленный из абсолютных величин его членов. Так же, как и для числовых действительных рядов с произвольными членами, легко доказать, что если сходится ряд , то обязательно сходится ряд . (|a_n| ≤ |z_n|, |b_n| ≤ |z_n|, поэтому ряды, образованные действительной и мнимой частями ряда , сходятся абсолютно). Если ряд сходится, а ряд расходится, то ряд называется условно сходящимся. Ряд - ряд с неотрицательными членами, поэтому для исследования его сходимости можно применять все известные признаки

17. Степенные ряды в комплексной области. Теорема Абеля и следствия к ней. Радиус сходимости.

Определение суммы числового ряда и признаки сходимости в комплексном области практически такие же, как в вещественном, с заменой абсолютной величины на комплексный модуль; исключение составляют признаки сходимости, в которых происходит сравнение на больше-меньше самих элементов ряда, а не их модулей.

Всякая дифференцируемая в точке   функция разлагается в окрестности этой точки в степенной ряд Тейлора:

Коэффициенты ряда вычисляются по обычным формулам. Этот ряд сходится к функции   в некотором круге радиуса   с центром в точке  , который служит аналогом интервала сходимости вещественного ряда. В этом круге ряд абсолютно сходится, а вне его расходится. При этом возможны 3 случая.

1. Ряд сходится в круге конечного и ненулевого радиуса.

2. Ряд сходится во всей комплексной плоскости, то есть 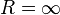 . Такие функции называются целыми.

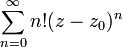3. Ряд сходится только в точке  . Пример:  . Такие точки   называются особыми для функции  . Неособые точки называются правильными. Внутренность круга сходимости состоит из правильных точек.

Граница круга сходимости содержит хотя бы одну особую точку. Отсюда следует, что радиус круга сходимости в точке   равен расстоянию от   до ближайшей к ней особой точки.

Теорема Абеля: если   — радиус круга сходимости степенного ряда, то в любом круге с тем же центром, но меньшего радиуса, ряд сходится равномерно.

теорема Абеля: Если степенной ряд сходится при некотором  , где -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что   Наоборот, если ряд расходится при  , то он расходится при всех значениях x таких, что 

Следствия теоремы Абеля.  1.    Если степенной ряд расходится в точке z₂ № z₀ , то он расходится и при " z: |z-z₀|>|z₂-z₀ |. (Предполагая противное, получим, что по тереме Абеля ряд должен сходится в " круге радиуса r <|z-z₀ |, в частности и в точке z ₂ , что противоречит условию.). 2. Круг сходимости. Радиус сходимости. Рассмотрим s up|z₁-z₀ |=R для " z₁ , где ряд сходится- точную верхнюю грань расстояний от точки z ₀ до точек z ₁ в которых сходится ряд  c_n(z-z₀)ⁿ . Если R , то для " z₂: |z₂-z₀ |>R ряд расходится. R=inf|z ₂-z₀ |=R для " z₂ , где ряд расходится. ПустьR>0, тогда наибольшей областью сходимости степенного ряда является круг |z-z ₀|<R - круг сходимости степенного ряда, число R>0- радиус сходимости степенного ряда. Внутри круга сходимости ряд сходится, вне- расходится, в точках границы |z-z₀ |=R   может как сходиться, так и расходиться.

Радиус сходимости

Если интервал сходимости представляется в виде  , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.  Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

или на основе признака Даламбера: