10. Определение интеграла функции комплексной переменной. Формула вычисления интеграла через криволинейные интегралы.

Понятие интеграла функции комплексной переменной вводится (так же, как и в действительной области) как предел последовательности интегральных сумм; функция при этом определена на некоторой кривой  .

Данная формула определяет криволинейный интеграл от функции комплексной переменной. Если выделить действительную и мнимую части функции  ,то интегральную сумму можно записать в виде двух слагаемых, которые будут являться интегральными суммами криволинейных интегралов второго рода от функций двух действительных переменных. Если   предположить непрерывной на  , то   будут также непрерывны на  , и, следовательно, будут существовать пределы соответствующих интегральных сумм. Поэтому, если функция  непрерывна на  , то предел в равенстве (2.43) существует, т.е. существует криволинейный интеграл от функции   по кривой   и имеет место формула

11. Основные свойства интеграла функции комплексной переменной.

12. Теорема Коши. Следствие к теореме Коши. Случай многосвязной области.

13. Первообразная и неопределенный интеграл функции комплексной переменной. Формула Ньютона-Лейбница.

14. Интеграл Коши. Интегральная формула Коши. Следствия к ней.

Формула называется интегральной формулой Коши или интегралом Коши. Если в качестве контура в выбрать окружность , то, заменяя и учитывая, что - дифференциал длины дуги , интеграл Коши можно представить в виде формулы среднего значения:

Следствия

Аналитичность голоморфных функций

В окрестности любой точки из области, где функция голоморфна, она совпадает с суммой степенного ряда:

причём его радиус сходимости не меньше радиуса круга с центром в точке , в котором функция голоморфна, а коэффициенты могут быть вычислены по интегральным формулам:

.

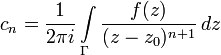Из этих формул следуют неравенства Коши для коэффициентов функций, голоморфных в круге :

Представимость голоморфных функций рядами Лорана в кольцевых областях

Если функция голоморфна в области вида , то в ней она представима суммой ряда Лорана:

причём коэффициенты могут быть вычислены по интегральным формулам:

а сам ряд Лорана сходится в к функции равномерно на каждом компакте из .

Теоремы о среднем для голоморфных функций

Если функция голоморфна в круге , тогда для каждого

а также если — круг радиуса с центром в , тогда

Из теорем о среднем следует принцип максимума модуля для голоморфных функций: если функция голоморфна в области и внутри её модуль имеет локальный максимум, тогда эта функция и есть константа.

15. Числовые ряды в комплексной области. Основные определения. Необходимый признак сходимости.

Основные определения и понятия.

Пусть мы имеем числовую последовательность , где .

Приведем пример числовой последовательности: .

Числовой ряд – это сумма членов числовой последовательности вида .

В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: .

называют общим членом числового ряда или k–ым членом ряда.

Для предыдущего примера общий член числового ряда имеет вид .

Частичная сумма числового ряда – это сумма вида , где n – некоторое натуральное число. называют также n-ой частичной суммой числового ряда.

К примеру, четвертая частичная сумма ряда есть .

Частичные суммы образуют бесконечную последовательность частичных сумм числового ряда.

Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии , то есть, будем иметь следующую последовательность частичных сумм: .

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

Необходимый признак сходимости Если ряд сходится, то его общий член стремится к нулю, т.е. . Отсюда следует, что если не равен нулю, то ряд расходится.