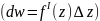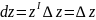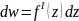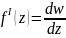1. Функции комплексной переменной. Основные понятия.

2. Предел и непрерывность функции комплексной переменной.

Определение: число w₀ называется пределом функции f(z) в точке z₀, если для любого эпсилант>0, есть g>0 (0<|z-z₀|<g), выполняется неравенство |f(z)-w₀|<эпсилант.

Следствие: если записать действительную и мнимую часть неравенства, то будет выглядеть так: lim u(x,y)=u₀ и lim v(x,y)=v₀ (w₀=u₀+iv₀)/

Замечание: теорема о пределах суммы, разности, произведения и частного для функции действительной переменной справедливы и для функции комплексной переменной.

Определение: пусть функция w=f(z) определена в точке z₀ и в некоторой ее окрестности, функция называется непрерывной в точке z₀, если предел функции в z₀ равен значению функции в z₀. Функция w=f(z) непрерывна в каждой точке области D называется непрерывной в области D (областью на комплексной плоскости называют множество точек, которые обладают свойствами открытости и связности).

Св-во открытости – каждая точка принадлежит множеству вместе с каждой ее окрестностью (внутренняя точка).

Св-во связности – множество связное, если любые 2 точки можно соединить линией/кривой, лежащей в этой области.

Граничные точки – это точки, в любой сколь угодно малой окрестности которой находятся как принадлежащие данному множеству точки, так и не принадлежащие.

Внешние точки – точки, некоторые окрестности которых не содержат ни одной точки данного множества.

Св-ва непрерывной функции:

1. модуль непрерывной функции комплексной переменной обладает теми же св-вами, что и функция действительной переменной; непрерывная функция на ограниченном множестве ограничена

2. непрерывная функция достигает наибольшего и наименьшего значения в точках множества

3. непрерывная функция принимает все промежуточные значения между наибольшим и наименьшим значениями

3. Определение, формула и свойства показательной функции комплексной переменной.

Число w называется показательной функцией, если w определяется формулой: w=ez=ex(cosy+isiny)

• если y=0, то w=ex

• выполняются все св-ва действий со степенями: 1) ez1+z2=ez1*ez2; 2) ez1-z2=ez1:ez2; 3) (ez1)n=enz1

• модуль |ez|=ex неравно 0, т.е. ez неравно 0

• lim ez=0 при Re z->-бесконечность и x->-0 и lim ez=бесконечности при Re z->-бесконечность и x->+бесконечность

• замечание: если x=0, а y=fi, то получим ф-ция Эйлера eifi=cosfi+isinfi и мы можем написать в показательной форме компл.числа: w=ez=ex*eifi fi=argz

• показательная функция является периодической с периодом 2пиi:

ez+2пиi=ez*e2пиi=ez(cos2пи+isin2пи)=ez

• значение функции не всегда положительное

4. Определение, формула и свойства логарифмической функции комплексной переменной.

5. Определение, формула и свойства степенной функции комплексной переменной.

6. Определение, формула и свойства тригонометрических функций комплексной переменной.

7. Определение, формула и свойства обратных тригонометрических функций комплексной переменной.

8. Дифференцирование функции комплексной переменной. Условия Эйлера-Даламбера. Правила дифференцирования.

9. Аналитическая функция. Правильные и особые точки. Дифференциал аналитической функции.

Однозначная функция w=f(z) называется аналитической в точке z (галаморфной), если она дифференцируема в некоторой окрестности этой точки. Функция f(z) называется аналитической в области D, если она дифференцируема в каждой точке области.

В точках плоскости, в которых функция f(z) аналитична, называются правильными точками, в которых не аналитична, называются особыми точкам функции.

Диференциалом аналитической функции в точке z называется главной частью приращения