Проверка адекватности регрессионной модели

Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным.

При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры характерны для отобранных условий: не являются ли полученные значения параметров результатами действия случайных получение значение параметров результатами действия случайных причин.

Значимость коэффициентов простой линейной регрессии (применительно к совокупности, у которых n < 30) осуществляют с помощью t- критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t- критерия для параметра а₀:

4.

для параметра а₁:

5.

где n- объем выборки;

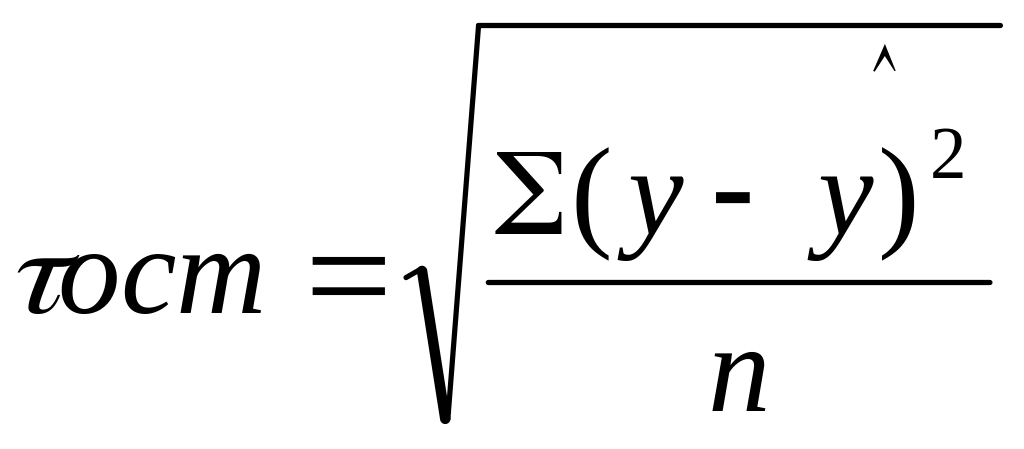- среднее квадратическое отклонение результативного признака у от выровненных значений ;

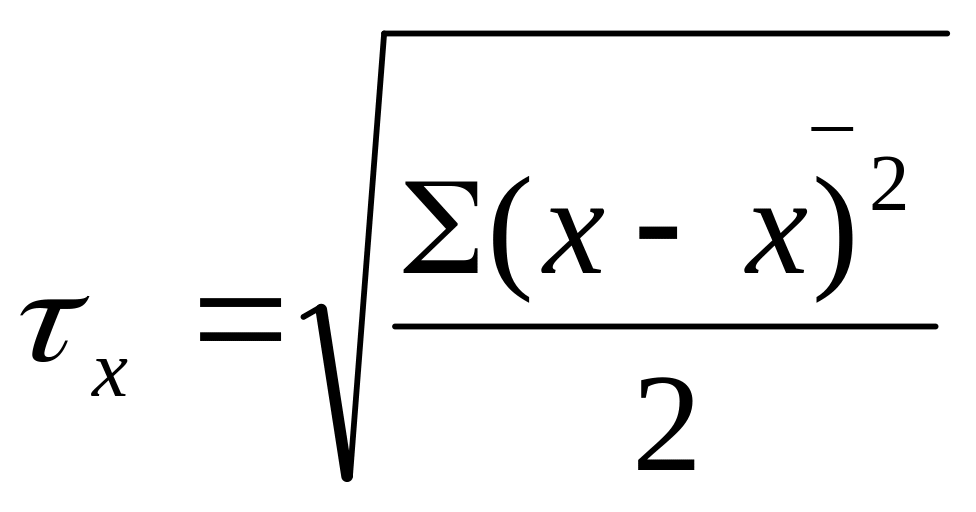или - среднее квадратическое факторного признака х от общей средней

Вычисление по формулам (4) и (5) значения, сравнивают с критическими t, которые определяют по таблице. Стьюдента с учетом принятого того уровня значимости х и числом степеней свободы вариации.

6

U=n-2

.

В социально – экономических 1нес-я1 уровень значимости х обычно принимают равным =0,05.

Параметр признается значимым (существенным) при условии, если t 1расч1 t таблица. В этом случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. Для проверки значимости коэффициентов регрессии исследуемого уравнения =4,0+0,6х исчислим t – критерий Стьюдента с V=10-2=8 степенями свободы.

Рассмотрим вспомогательную таблицу. Расчетные значения, необходимые для исчисления ,

1	2	3	4	5	6
-3,3	10,89	-2,7	7,29	-0,6	0,36
-2,3	5,29	-2,1	4,41	-0,2	0,04
-1,3	1,69	-1,5	2,25	0,2	0,04
-0,3	0,09	-0,9	0,81	0,6	0,36
-0,3	0,09	-0,3	0,09	0,0	0,0
0,7	0,49	0,3	0,09	0,4	0,16
0,7	0,49	0,9	0,81	-0,2	0,04
1,7	2,89	1,5	2,25	0,2	0,04
2,7	7,29	2,1	4,41	0,6	0,36
1,7	2,89	2,7	7,29	-1,0	1,0
	32,10	-	29,70		2,40

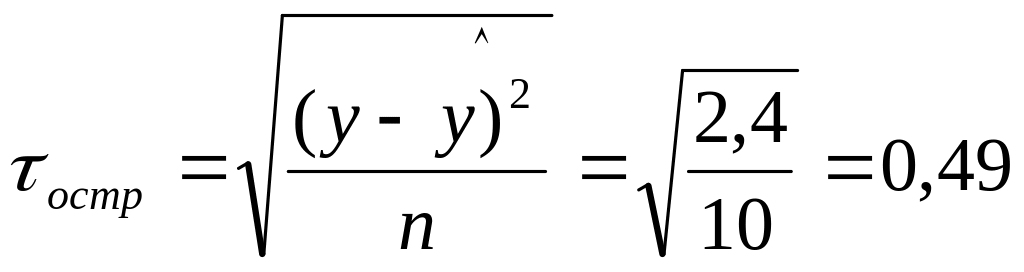
Расчетные значения t – критерия Стьюдента:

По таблице распределения Стьюдента для V=8 находили критическое значение t- критерия: t_табл=3,307 при V=8, =0,05.

Поскольку t_рас > t_табл, оба параметра а₀, а₁признаются значимыми.

Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.

Теснота связи может быть измерена эмпирическими корреляционными отношениями h _э: - межгрупповая дисперсия.

Теоретическое корреляционное отношение h представляет собой относительную величину.

12.

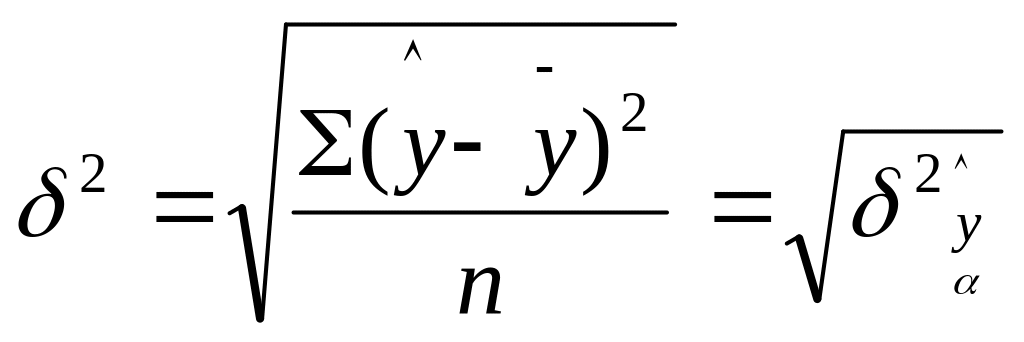
13.

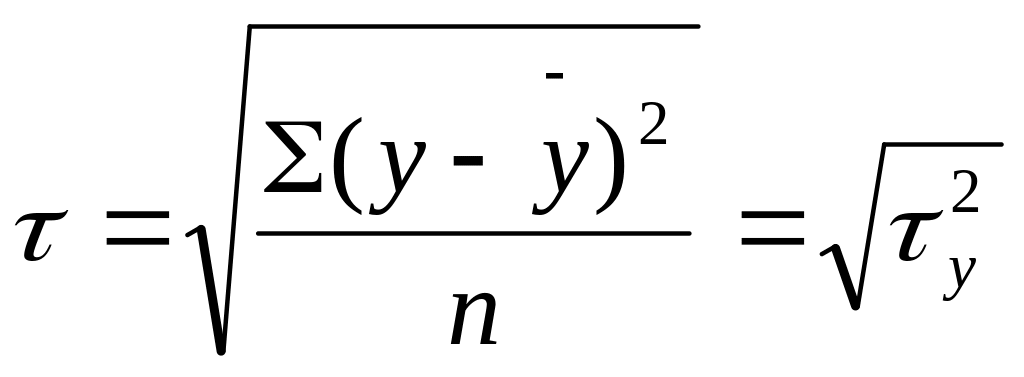
14. Тогда

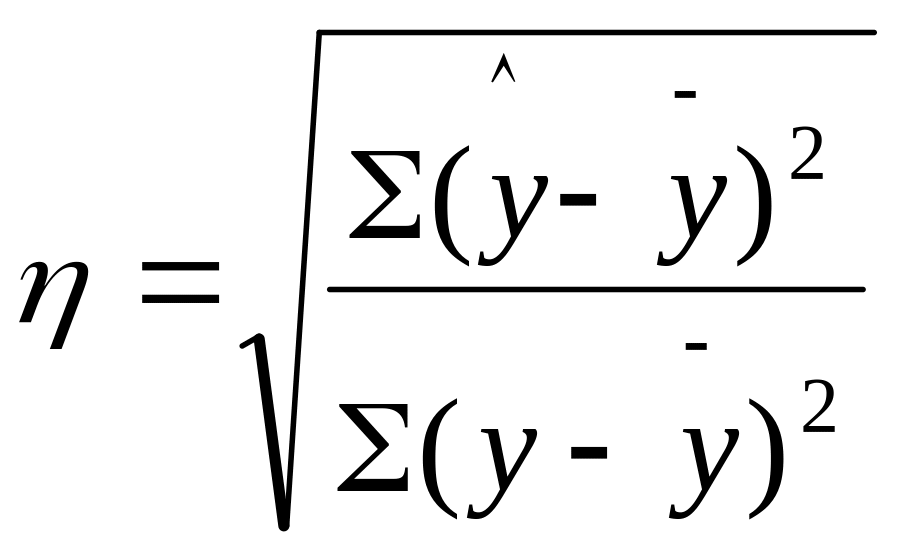
Изменение значения h объясняется влиянием факторного признака.

В основе корреляционного отношения лежит правило сложения дисперсией, т.е.

15. , где - отражает вариацию у за счет всех остальных факторов кроме х т.е. являются остаточной дисперсией

Тогда формула теоретического корреляционного отношения примет вид:

16.

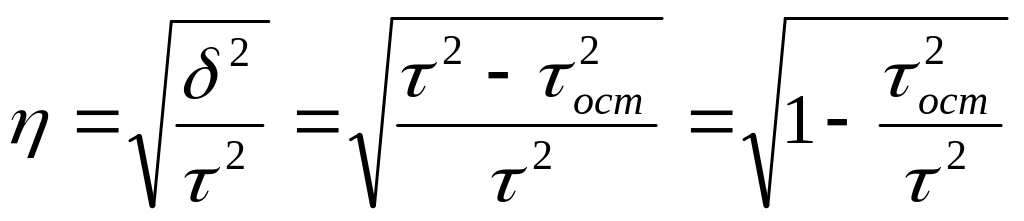
17. или 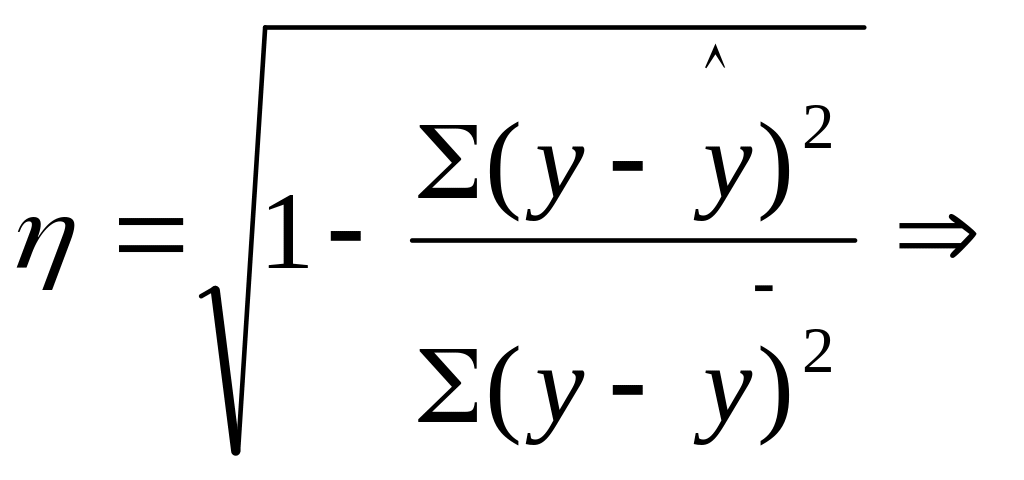под корень коэффициент детерминации (меры определяем ости, причинности).

Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака – фактора.

Как видно из формул (16) и (17), корреляционное отношение может находиться в пределах от 0 до 1 (0≤ ≤ 1), чем ближе корреляционное отношение к 1 тем связь между признаками теснее.

Рассмотрим расчет теоретического корреляционного отношения как меры тесноты связи на примере, 1рас-ком1 в таблице 1 и 2 для которого по уравнению прямой регрессии =4+0,6х найдены значения дневной 1выр-и1 каждого рабочего.

Теоретическое 1кар-ое1 1от-е1 рассчитываем двумя способами:

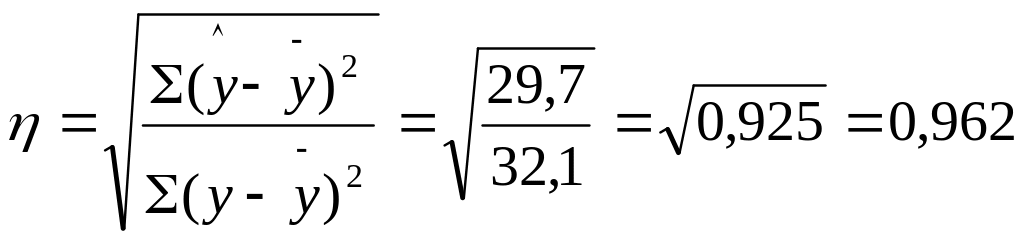
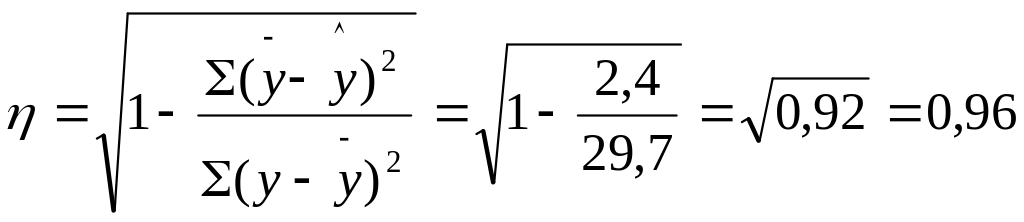
Коэффициент детерминации равен 0,925. Отсюда заключаем, что 92,5% общей вариации выработки в изучаемой бригаде обусловлено вариацией фактора – стажа работы рабочих (и только 7,5%, общей вариации нельзя объяснить изменением стажа работы).

Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи – линейный коэффициент корреляции (был предложен английским математиком К. Пирсоном).

18. Z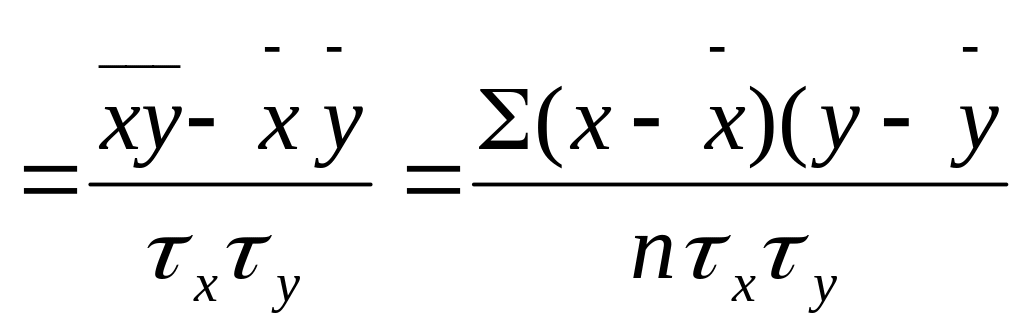

n – число наблюдений.

Для практических вычислений при малом числе наблюдений (n ≤ 20:30) л.к. к удобнее исчислять по следующей формуле:

19. Z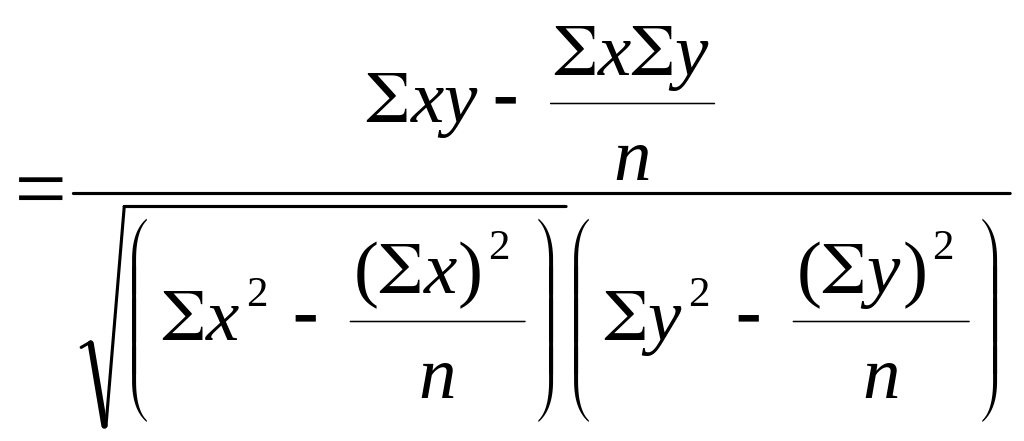

Значение ЛКК важно для 1ис-я1 социально – экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значение в интервалы:

-1≤ z ≤ +1

1отр-ое1 значения указывают на обратную связь, положительные – на прямую связь. При z =0 линейная связь отсутствует.

Используя данные таблицы 1 и расчетом ЛКК по формуле (19).

ч

Квадрат линейного коэффициента корреляции z² 1поз-я1 линейным коэффициентом детерминации.

0≤ z² ≤ 1

Значения и z совпадают только при наличии прямолинейной связи. Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что разность квадратов и z² не превышает 0,1 то гепотезу о прямолинейной форме связи можно считать подтвержденной.