2.5 Безразмерные показатели.

Существуют способы изображения характеристик в относи­тельных системах координат, такие характеристики называют­ся безразмерными и применимы для целой серии геометри­чески подобных нагнетателей. Относительные, безразмерные координаты обозначаются горизонтальной черточкой над бук­вой, обозначающей рабочий параметр нагнетателя: . КПД являются относительными величинами и по­этому чертой не отмечаются.

Пользуясь уравнением Эйлера (2.5), можно показать, что существует величина , определяемая равенством

, (2.9)

называемая безразмерным напором или коэффици­ентом напора и постоянная для целой серии подобных дина­мических нагнетателей (вентиляторов, насосов).

Аналогичным путем могут быть установлены безразмерное давление (коэффициент давления)

(2.10)

и безразмерная мощность (коэффициент мощности)

. (2.11)

Коэффициент полезного действия является безразмерным параметром

(2.12)

На рис. 2.6 в качестве примера дана безразмерная характерис­тика вентилятора, применяемого для подачи воздуха в топку котлов большой производительности.

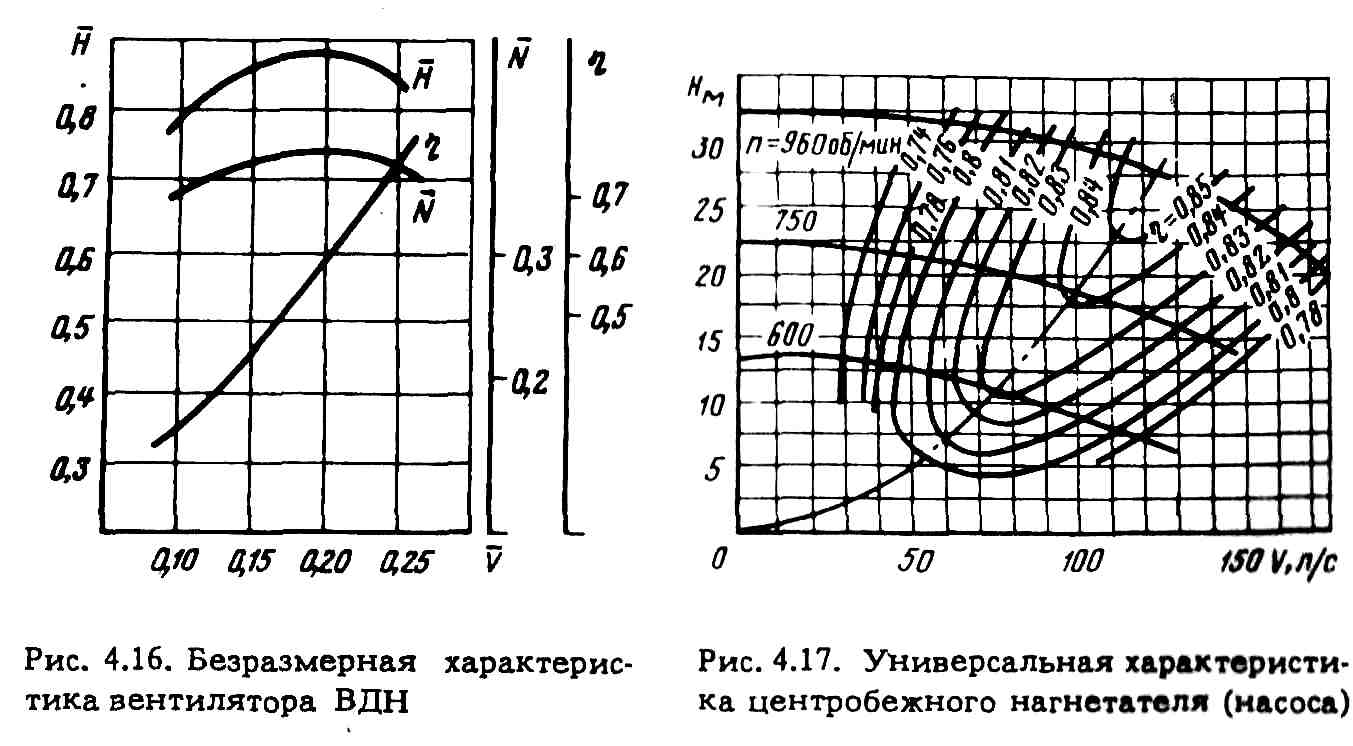
Рис. 2.6. Безразмерная характеристика вентилятора ВДН

Наиболее полное представление о рабочих параметрах дина­мических нагнетателей дают их универсальные характерис­тики.

Если на характеристику нагнетателя (насоса, вентилятора) при п = var нанести точки с одинаковыми КПД, определяемы­ми соотношением

,

и соединить эти точки плавными линиями, то получим уни­версальную (топографическую) характеристику с изолиниями КПД. При графическом изображении функциональных зависимостей изолини­ями называют такие линии, для всех точек которых числовое значение дан­ной функции постоянно.

На рис. 2.7 в качестве примера дана универсальная харак­теристика низко-напорного центробежного насоса.

Рис. 2.7. Универсальная характеристика центробежного нагнетателя (насоса)

2.6 Теоретические и действительные характеристики динамических нагнетателей.

Характеристиками центробежной машины называют графически изображенные зависимости

(2.13)

Если эти зависимости даны при , то они явля­ются характеристиками при постоянной частоте вращения; если же они даны при , то их называют характерис­тиками при переменной частоте вращения.

Наиболее важной характеристикой является зависи­мость между напором и подачей (или давлением и пода­чей).

Для центробежной машины с заданными геометричес­кими размерами при

Рис. 2.8. Теоретические характеристики центробежных машин при различных углах

При построения характеристики центробежной машины при предполагается изменение аргумента пу­тем изменения открытия запорного органа на выходном патрубке машины. Такой процесс называется дросселированием, а сами характеристики  дроссельными кривыми.

Независимо от формы рабочей лопасти, определяемой углом , теоретический напор при (полное закрытие регулирующей задвижки) определяется однозначно диаметром рабочего колеса и его частотой вра­щения .

Так как при теоретическая характеристи­ка машины получится в виде прямой, параллельной оси аб­сцисс (рис. 2.8).

Лопасти, отогнутые назад, характеризуются углом < , характеристика такой машины представится наклонной линией, расположенной ниже характеристики ма­шины с = . Напротив, если машина имеет лопасти с  (отогнутые вперед) то теоретическая характеристика для такого случая располагается выше горизонтальной характеристики при . Из рис. 2.8 видно, что при заданной подаче тео­ретический напор тем выше, чем больше рабочая лопасть отогнута вперед.

Достижение заданных теоретического напора и подачи центробежной машины при рабочих колесах с различными углами требует различных окружных скоростей на выходе из рабочего колеса или при одинаковом диаметре колес различных частот вращения.

Для получения заданного теоретического напора при одинаковом диаметре рабочих колес наименьшей частотой вращения должно обладать колесо с лопастями, загнутыми вперед, а наибольшей  колесо с лопастями, загнутыми назад. По уравнению мож­но выяснить форму характери­стики теоретической мощности центробежной машины:

. (2.14)

Эта характеристика может быть представлена графиче­ски для различных значений при постоянных значениях .

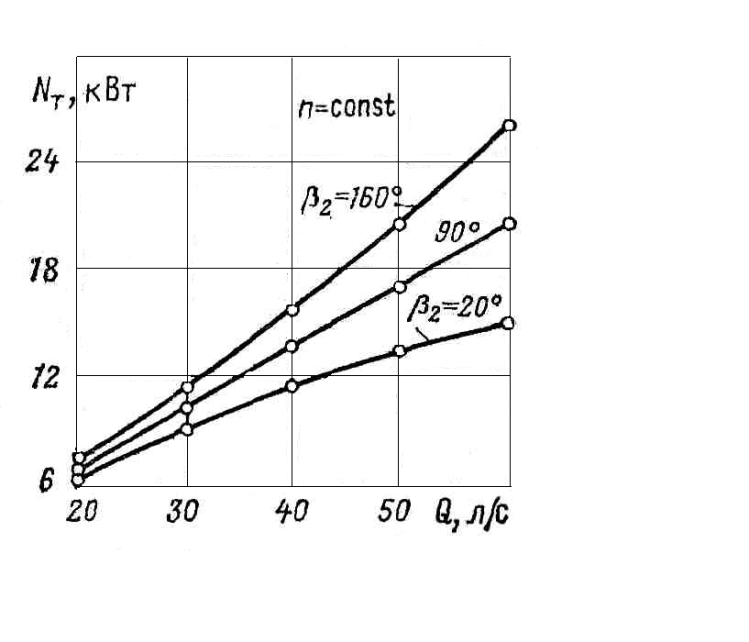
На рис. 2.9 показаны теоретические характеристики мощности для углов =20; 90 и 160°, при n=1000 об/мин, =0,5 м и =0,03 м (центробежный насос).

Рис. 2.9. Теоретические характеристики мощности при различных значениях угла

При изменении подачи машины потери напора меняют­ся, во-первых, вследствие изменения сопротивления про­точной полости, пропорционального квадрату средней ско­рости потока, во-вторых, по причине изменения направле­ния скорости на входе в межлопастные каналы. Последнее обусловливает удар жидкости (газа) о входные кромки лопастей и образование в потоке вихревых зон. В резуль­тате этого характеристика действительного напора распо­лагается ниже характеристики теоретического напора.

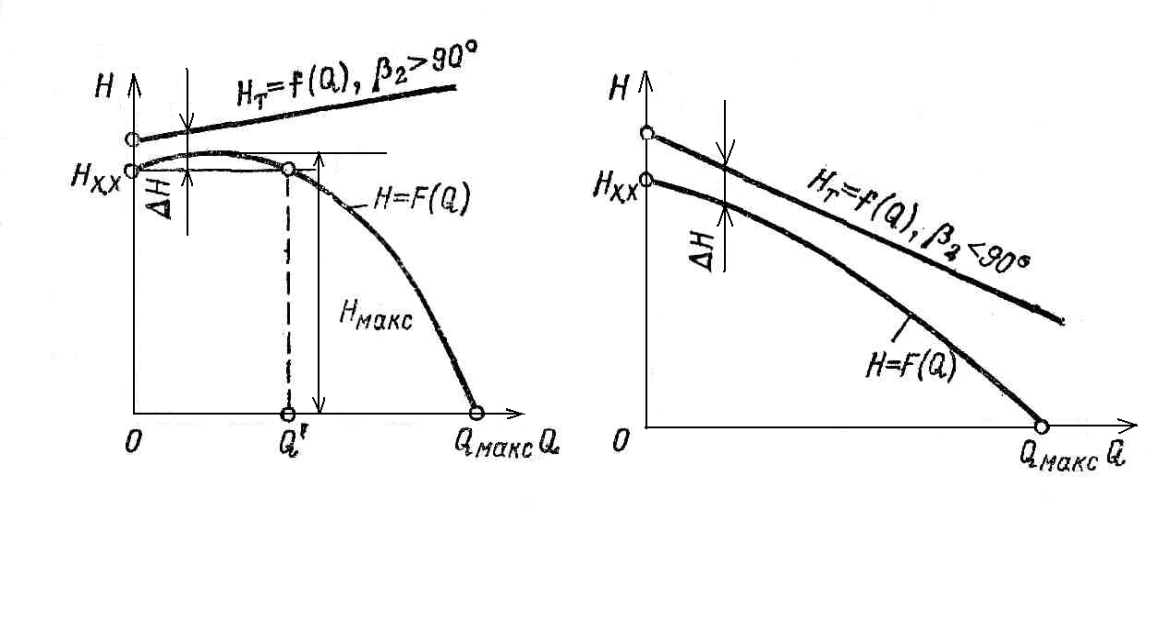
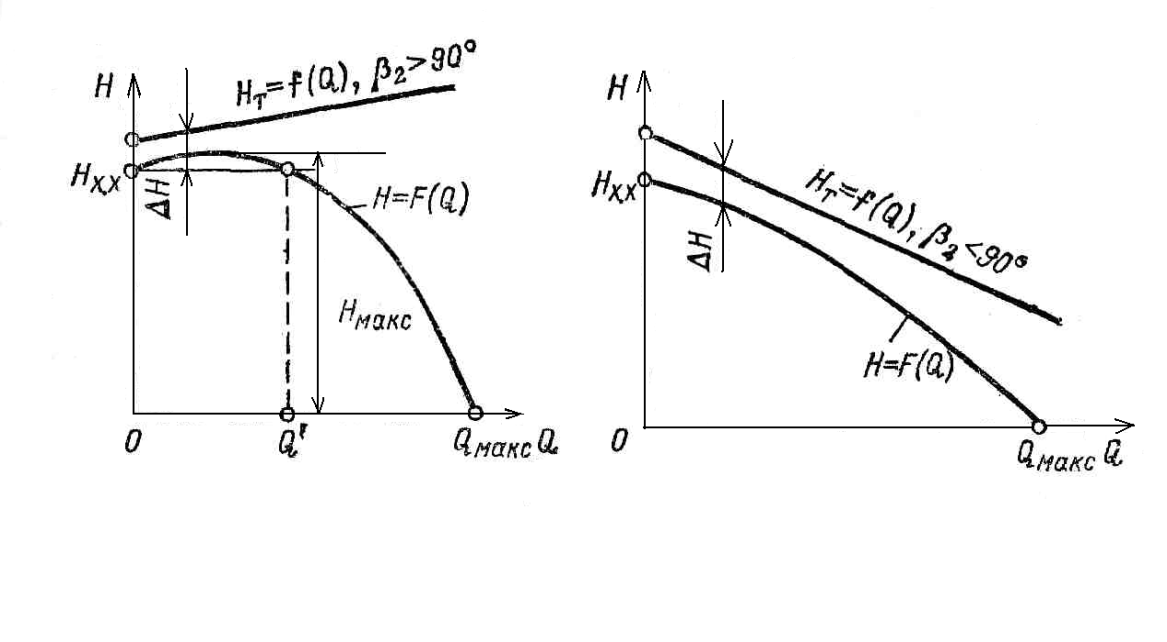
Рис. 2.10. Действительная характеристика при

В зависимости от значения лопастного угла и конст­руктивных особенностей проточной полости центробежной машины действительная характеристика может иметь две типичные формы.

Характеристика, представленная на рис. 2.10, типична для >90°. Особенностью такой характеристики является наличие максимума и, следовательно, неоднозначность за­висимости для данной машины в пределах напо­ров от до . Машины с характеристикой такого типа, как позднее будет показано, могут работать неустой­чиво, самопроизвольно изменяя подачу. Это является от­рицательным свойством машины, и поэтому такой тип ха­рактеристики нежелателен.

Рис. 2.11. Действительная характеристика при

Другая форма характеристики, представленная на рис. 2.11, свойственна центробежным машинам с <90° при рациональной конструкции проточной части.

Действительная характеристика мощности машины может быть получена из теоретических характеристик пу­тем вычитания (при данных подачах) из значений теорети­ческой мощности ее потерь. При этом характер зависимо­сти мощности от подачи в основном сохранится: действи­тельная мощность машины будет возрастать с увеличением подачи. Однако вследствие неодинакового относительного влияния потерь на полную мощность линия действитель­ной мощности отклоняется от линии теоретической мощности; она представится слегка изогнутой кривой. Теорети­ческая мощность при подаче, равной нулю, также равна нулю. Действительная же мощность при (при закры­том дросселе) равна мощности холостого хода , затра­чиваемой на покрытие потерь мощности в этом режиме. По­тери мощности на холостом ходу обусловлены циркуляци­онными потоками в проточной части машины, особенно в рабочем колесе, дисковым трением о жидкость (газ), ме­ханическим трением в уплотнениях и подшипниках машины.

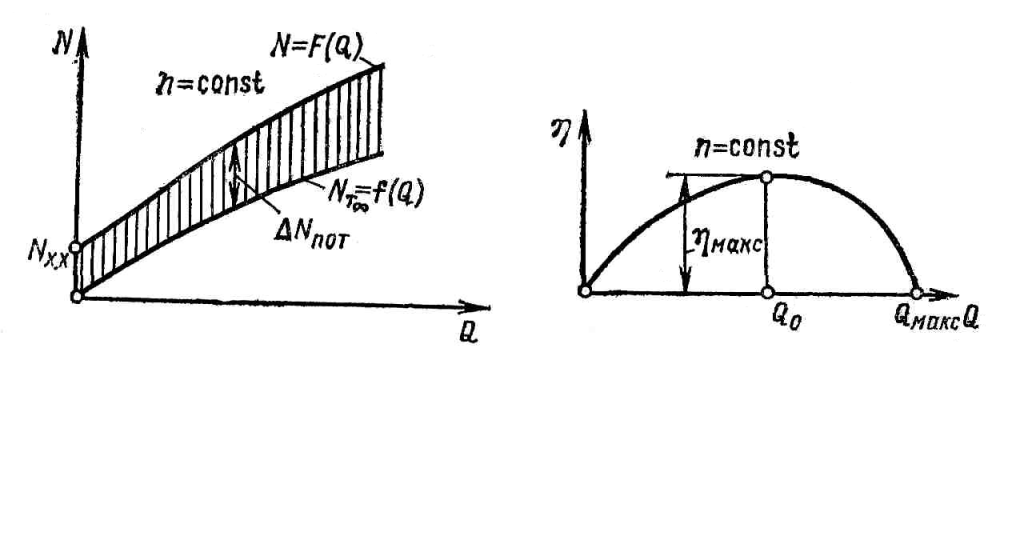
Рис. 2.12. Характеристики теоретической и действительной мощностей центробежной машины

Рис. 2.13. Характеристика КПД центробежной машины

Все указанное приводит к форме характеристик дей­ствительной мощности, показанной на рис. 2.12.

По характеристикам действительного напора и дейст­вительной мощности определяется КПД центробежной машины. Из уравнения получим

_.

Очевидно, КПД равен нулю при или , пото­му что при всех режимах работы машины . В преде­лах между и (рис. 2.13) КПД машины до­стигает максимального значения.

Режим машины, при котором ее КПД максимален, на­зывают оптимальным; при этом затраты мощности для со­здания напора и подачи реализуются в машине с наи­лучшим энергетическим эффектом, т.е. наиболее эконо­мично².