14 Билет

Числовой ряд – это сумма членов числовой последоват-и вида

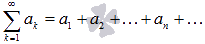
Операции на числовыми рядами(?)

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

• Их суммой называется ряд 

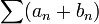
• Их произведением по Коши называется ряд 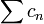 , где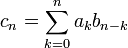 

Простейшие свойства сходящихся рядов.

1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.

2. Если ряд 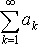сходится, то .

3. Если ряд сходится, то сходится ряд и имеет место равенство .

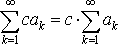4. Если ряды и 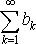сходятся, то сходится и ряд 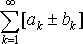имеет место равенство

.

5. Если ряд сходится, то .

Отсюда следует

Признак расходимости ряда. Если , то ряд расходится.

15 Билет

Основные понятия теории вероятности.

Вер-ть некоторого события – это числовая характеристика некоторого события, степени возможности осуществеления данного события

Теория вер-ей – матем наука, изучающ законом-ти случ явл-й и события, способные многократно повторяться при воспр-ии опред комплекса условий

Результат эксперимента или наблюдения, который при данном усл-ии может произойти или не произойти назыв случ событием.

Cлучайная величина – это величина, значение которой зависит от случая.

Свойства вероятностей.

Событие назыв достоверным, если оно при реализ-ии данного компл-а условий непременно произойдет

Событие назыв невозможн, если оно заведомо не может произойти при реализ-ции данных условий

Суммой событий А и В назыв А+В, состоящ в том, что произошло хотя бы одно событие

Произв-е событий А и В назыв А*В состоящ в совместном осущ-ии А и В

События А и В несовместны, если они не могут произойти одновременно.

Вер-ть достоверного события равнв 100 %, вер-ть невозможн соб-я равна 0.

Классическое определение вероятности.

Пусть n– число всех элементарных исходов, m– число тех из них, которые благоприятны событию А. Тогда вер-ю события А называется Р(А) = m/n

Статистическое определение вероятности.

Пусть проводится некоторое испытание в рез-те которого может произойти соб-е А n раз, а соб-е А появляется m раз, тогда число М(А)=m/n назыв статистич вер-ю

Геометрическое определение вероятности.

Пусть на плоскости дана плоскость Д. В ней содержится область d, ее площадь s(d), тогда вер-ть события А (точка попадает в d = числу Р(А) = s(d)/S(D)

Теоремы сложения и умножения вероятностей.

Вер-ть суммы попарно несовм соб-й = сумме вер-й этих соб-й, те P(A+B)=P(A)+P(B), где А и В несовместны

Вер-ть суммы совм соб-й =сумме вер-й этих событий без вер-и их совмо сущ-я, те P(A+B)=P(A)+P(B)-P(A*B)

Когда вер-ть появл-я соб-я В зависит от того, произошло или нет соб-е А, то вер-тьпоявл-я соб-я В назыв условной вер-ю.

Вер-ть произв-я 2 зависим событий = произв-ю одного из этих событий на условн вер-ть другого, при условии, что 1 событие произошло, те P(A+B)=P(A)*P(BIAI)

В-ть произв-я 2 незав событий = произв-ю вер-ей этих соб-й P(A*B)=P(A)*P(B)

Формула полной вероятности и формула Бейеса.

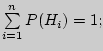
П.в: где - вероятность гипотезы , - условная вероятность события при выполнении гипотезы ( .

Бейса: Пусть событие происходит одновременно с одним из несовместных событий . Требуется найти вероятность события , если известно, что событие произошло.

На основании теоремы о вероятности произведения двух событий можно написать

Откуда

или