10 Билет

Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций.

Формулы,основные правила дифференцирования

Приложения дифференциального исчисления.(?)

Основные теоремы дифференциального исчисления.

Теорема Ролля. Между двумя различными корнями дифференцируемой функции содержится по меньшей мере один корень ее производной.

Теорема Коши. Если функция f (x) непрер на отрезке [a; b] и принимает на его концах знач-я разных знаков, то на отрезке [a; b] имеется хотя бы один 0 функции f. При этом, если функция строго монот-а на этом отрезке, то она принимает значение 0 лишь 1раз.

Точка экстремума – точка, в которой функция имеет

максимум или минимум. Точкой макс ф-и f(х) назыв точка х0, если существует окрестность точки х0 – такая, что выполняется неравенство f(х) ≤ f(х0) для всех х из этой окрестности.

11 Билет

Неопределенный интеграл-множество всех первообразных функции.

Функция F(x) называется первообразной для функции F(x) на некотором промежутке, если для всех X этого промежутка F(x)=g(x).

Линейные св-ва интегралов:

1.дифференциал от неопределенного интеграла=подынтегральному выражению, а производная неопред интеграла=подынтегр функции.

2.неопред интеграл от диффер-ла некоторой функции=сумме этой функции и произвольной постоянной.

3.пост множитель можно вынести за знак интегр-ла.

4.неопред интегр от алгебр-й суммы конечного числа непрерывных функций=алгебр сумме интегр-ов от слагаемых функции.

Метод интегрирования подстановкой(заменой переменной). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводится.

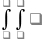
12 Билет

Опред интеграл-монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция, а вторая - область в множестве задания этой функции.

Формула Ньютона-Лейбница

Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: .

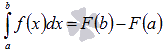Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления

Линейные св-ва:

1.если C-const и функцию f(x) интегрируема на [a;b], то C можно вынести за знак интеграла.

2.если функции f1(x) и f2(x) интегрируемы на [a;b], то интеграл от суммы=сумме интегралов.

Геометрич прилож опред интегр.

Если f(x) >0 на отрезке [a,b], то равен площади криволинейной трапеции ABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y = f(x).

13 Билет

Диффер уравнения-уравнен, связывающие независ перемен-ю, искомую функцию и её производную.

Дифференциальное уравнение 1го порядка содержит:

1) независимую переменную

2) функцию

3) первую производную функции

Решить ДУ– это значит, найти множество функций, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.

Дифференциальным уравнением с разделяющимися переменными в высшей математике называется дифференциальное уравнение первого порядка вида