
№4Предельный
признак Даламбера.Предельный
признак Даламбера является следствием
из приведенного выше признака Даламбера.
Если
существует предел
Если
для ряда
Следствие.
Если существует предел
Вывод:
ряд сходится. Пример.
Определить сходимость ряда
Т.е.
признак Коши не дает ответа на вопрос
о сходимости ряда. Проверим выполнение
необходимых условий сходимости. Как
было сказано выше, если ряд сходится,
то общий член ряда стремится к нулю. таким
образом, необходимое условие сходимости
не выполняется, значит, ряд расходится.
№ 5Интегральный
признак Коши. Если
(х)
– непрерывная положительная функция,
убывающая на промежутке
[1;),
то
ряд (1)
+ (2)
+ …+ (n)
+ … =
Пример.
Ряд
Следствие.
Если f(x)
и (х)
– непрерывные функции на интервале
(a,
b]
и
№6
Знакочередующиеся
ряды.Знакочередующийся
ряд можно записать в виде: где
Признак
Лейбница. Если
у знакочередующегося ряда
абсолютные величины ui
убывают
Абсолютная
и условная сходимость рядов. Рассмотрим
некоторый знакопеременный ряд (с членами
произвольных знаков).
и
ряд, составленный из абсолютных величин
членов ряда (1):
Доказательство.
Ряд (2) является рядом с неотрицательными
членами. Если ряд (2) сходится, то по
критерию Коши для любого >0
существует число N,
такое, что при n>N
и любом целом p>0
верно неравенство: По
свойству абсолютных величин: То
есть по критерию Коши из сходимости
ряда (2) следует сходимость ряда (1). Определение.
Ряд
называется
абсолютно
сходящимся,
если сходится ряд
![]() ,
то при
< 1 ряд сходится, а при
> 1 – расходится. Если
= 1, то на вопрос о сходимости ответить
нельзя. Признак
Коши. (радикальный признак)
,
то при
< 1 ряд сходится, а при
> 1 – расходится. Если
= 1, то на вопрос о сходимости ответить
нельзя. Признак
Коши. (радикальный признак)![]() с
неотрицательными членами существует
такое число q<1,
что для всех достаточно больших n
выполняется неравенство
с
неотрицательными членами существует
такое число q<1,
что для всех достаточно больших n
выполняется неравенство![]() ,
то ряд
сходится,
если же для всех достаточно больших n
выполняется неравенство
,
то ряд
сходится,
если же для всех достаточно больших n
выполняется неравенство![]() то
ряд
расходится.
то
ряд
расходится.![]() ,
то при <1
ряд сходится, а при >1
ряд расходится. Пример.
Определить сходимость ряда
,
то при <1
ряд сходится, а при >1
ряд расходится. Пример.
Определить сходимость ряда
![]() .
.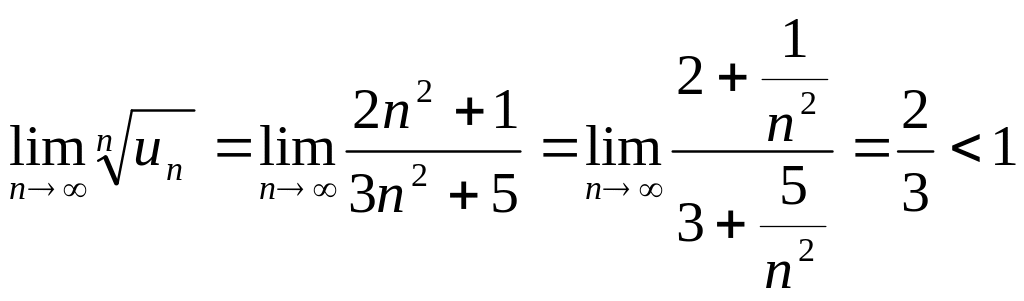
![]() .
.![]()
![]() ,
,![]() и несобственный интеграл
и несобственный интеграл
![]() одинаковы в смысле сходимости.
одинаковы в смысле сходимости.![]() сходится при >1
и расходится 1
т.к. соответствующий несобственный
интеграл
сходится при >1
и расходится 1
т.к. соответствующий несобственный
интеграл
![]() сходится при >1
и расходится 1.
Ряд
сходится при >1
и расходится 1.
Ряд
![]() называется общегармоническим
рядом.
называется общегармоническим
рядом.![]() то интегралы
то интегралы
![]() и
и
![]() ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.![]()
![]()
![]() и общий член стремится к нулю
и общий член стремится к нулю
![]() ,
то ряд сходится.
,
то ряд сходится.![]() (1)
(1)![]() (2)Теорема.
Из
сходимости ряда (2) следует сходимость
ряда (1).
(2)Теорема.
Из
сходимости ряда (2) следует сходимость
ряда (1).![]()
![]()
![]()
![]() . Очевидно,
что для знакопостоянных рядов понятия
сходимости и абсолютной сходимости
совпадают. Определение.
Ряд
называется
условно
сходящимся,
если он сходится, а ряд
расходится.
. Очевидно,
что для знакопостоянных рядов понятия
сходимости и абсолютной сходимости
совпадают. Определение.
Ряд
называется
условно
сходящимся,
если он сходится, а ряд
расходится.
№10
Действия
со степенными рядами. 1)
Интегрирование степенных рядов. Если
некоторая функция f(x)
определяется степенным рядом:
Производная
функции, которая определяется степенным
рядом, находится по формуле 3)
Сложение, вычитание, умножение и деление
степенных рядов. Сложение
и вычитание
степенных рядов сводится к соответствующим
операциям с их членами:
Коэффициенты
сi
находятся по формуле: Для
определения коэффициентов qn
рассматриваем произведение
![]() ,
то интеграл от этой функции можно
записать в виде ряда:
,
то интеграл от этой функции можно
записать в виде ряда:![]()
Дифференцирование степенных рядов.
![]()
![]() Произведение
двух степенных рядов выражается
формулой:
Произведение
двух степенных рядов выражается
формулой:![]()
![]() Деление
двух
степенных рядов выражается формулой:
Деление
двух
степенных рядов выражается формулой: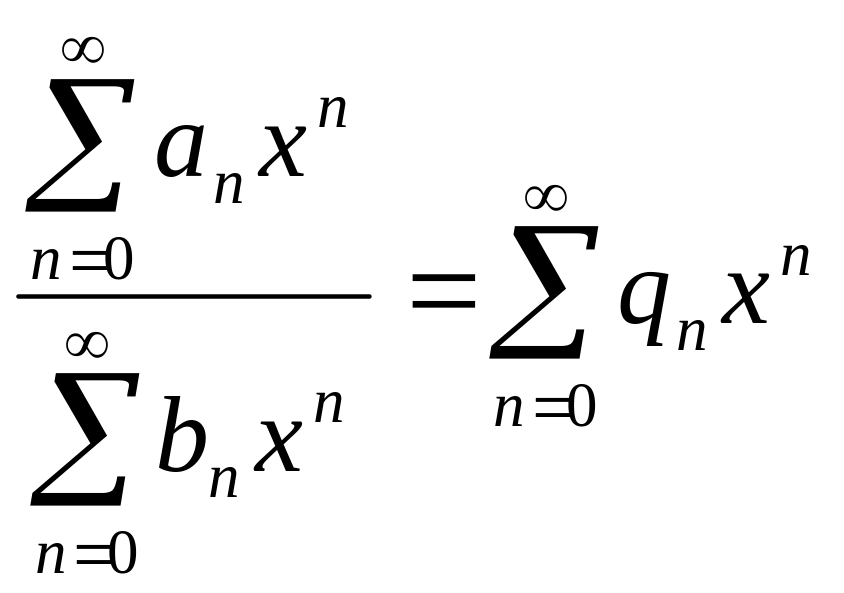
![]() ,
полученное из записанного выше равенства
и решаем систему уравнений:
,
полученное из записанного выше равенства
и решаем систему уравнений:![]()
№8Степенные
ряды. Определение.
Степенным
рядом называется
ряд вида
Теоремы
Абеля. Теорема.
Если
степенной ряд
сходится при x
= x1
, то он сходится и притом абсолютно для
всех
Доказательство.
По условию теоремы, так как члены ряда
ограничены, то
где
k-
некоторое постоянное число. Справедливо
следующее неравенство: Из
этого неравенства видно, что при x<x1
численные величины членов нашего ряда
будут меньше ( во всяком случае не больше
) соответствующих членов ряда правой
части записанного выше неравенства,
которые образуют геометрическую
прогрессию. Знаменатель этой прогрессии
Поэтому
на основании признака сравнения делаем
вывод, что ряд
Следствие.
Если при х
= х1
ряд расходится, то он расходится для
всех
Таким
образом, для каждого степенного ряда
существует такое положительное число
R,
что при всех х
таких, что
Отметим,
что этот интервал может быть как
замкнутым с одной или двух сторон, так
и не замкнутым.
Радиус
сходимости может быть найден по формуле: Теорема.
Если степенной ряд
сходится для положительного значения
х=х1
, то он сходится равномерно в любом
промежутке внутри
№9
Если при х
= х1
ряд расходится, то он расходится для
всех
. Таким
образом, для каждого степенного ряда
существует такое положительное число
R,
что при всех х
таких, что
ряд абсолютно сходится, а при всех
ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
Отметим, что этот интервал может быть
как замкнутым с одной или двух сторон,
так и не замкнутым. Радиус сходимости
может быть найден по формуле:
Пример.
Найти область сходимости ряда
Находим
радиус сходимости
№7
Абсолютная и условная сходимость рядов. Рассмотрим
некоторый знакопеременный ряд (с членами
произвольных знаков).
(1) и
ряд, составленный из абсолютных величин
членов ряда (1):
(2)Теорема.
Из
сходимости ряда (2) следует сходимость
ряда (1). Доказательство.
Ряд (2) является рядом с неотрицательными
членами. Если ряд (2) сходится, то по
критерию Коши для любого >0
существует число N,
такое, что при n>N
и любом целом p>0
верно неравенство:
По
свойству абсолютных величин: То
есть по критерию Коши из сходимости
ряда (2) следует сходимость ряда (1). Определение.
Ряд
называется
абсолютно
сходящимся,
если сходится ряд
.
Очевидно, что для знакопостоянных
рядов понятия сходимости и абсолютной
сходимости совпадают. Определение.
Ряд
называется
условно
сходящимся,
если он сходится, а ряд
расходится.
№19Повторение
испытаний. Формула Бернулли. Если
производится некоторое количество
испытаний, в результате которых может
произойти или не произойти событие А,
и вероятность появления этого события
в каждом из испытаний не зависит от
результатов остальных испытаний, то
такие испытания называются независимыми
относительно события А.Допустим,
что событие А наступает в каждом
испытании с вероятностью Р(А)=р.
Определим вероятность Рт,п
того, что в результате п
испытаний событие А наступило ровно т
раз.Эту вероятность в принципе можно
посчитать, используя теоремы сложения
и умножения вероятностей, как это
делалось в рассмотренных выше примерах.
Однако, при достаточно большом количестве
испытаний это приводит к очень большим
вычислениям. Таким образом, возникает
необходимость разработать общий подход
к решению поставленной задачи. Этот
подход реализован в формуле Бернулли.
(Якоб Бернулли (1654 – 1705) – швейцарский
математик) Пусть
в результате п
независимых испытаний, проведенных в
одинаковых условиях, событие А наступает
с вероятностью Р(А)
= р,
а противоположное ему событие
Вероятность
каждой комбинации равна произведению
вероятностей
Применяя
теорему сложения вероятностей
несовместных событий, получаем формулу
Бернулли Формула
Бернулли важна тем, что справедлива
для любого количества независимых
испытаний, т.е. того самого случая, в
котором наиболее четко проявляются
законы теории вероятностей
№23При
рассмотрении нормального закона
распределения выделяется важный частный
случай, известный как правило
трех сигм. Запишем
вероятность того, что отклонение
нормально распределенной случайной
величины от математического ожидания
меньше заданной величины : Это
правило называется правилом
трех сигм. Не
практике считается, что если для какой
– либо случайной величины выполняется
правило трех сигм, то эта случайная
величина имеет нормальное распределение.
![]() Для
исследования на сходимость степенных
рядов удобно использовать признак
Даламбера.
Для
исследования на сходимость степенных
рядов удобно использовать признак
Даламбера.![]() .
.![]()
![]()
![]() по условию теоремы меньше единицы,
следовательно, эта прогрессия представляет
собой сходящийся ряд.
по условию теоремы меньше единицы,
следовательно, эта прогрессия представляет
собой сходящийся ряд.![]() сходится, а значит ряд
сходится, а значит ряд
![]() сходится абсолютно.Таким образом, если
степенной ряд
сходится
в точке х1,
то он абсолютно сходится в любой точке
интервала длины 2
сходится абсолютно.Таким образом, если
степенной ряд
сходится
в точке х1,
то он абсолютно сходится в любой точке
интервала длины 2![]() с центром в точке х
= 0.
с центром в точке х
= 0.![]() .
.![]() ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех
![]() ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.![]()
![]() .
.![]()
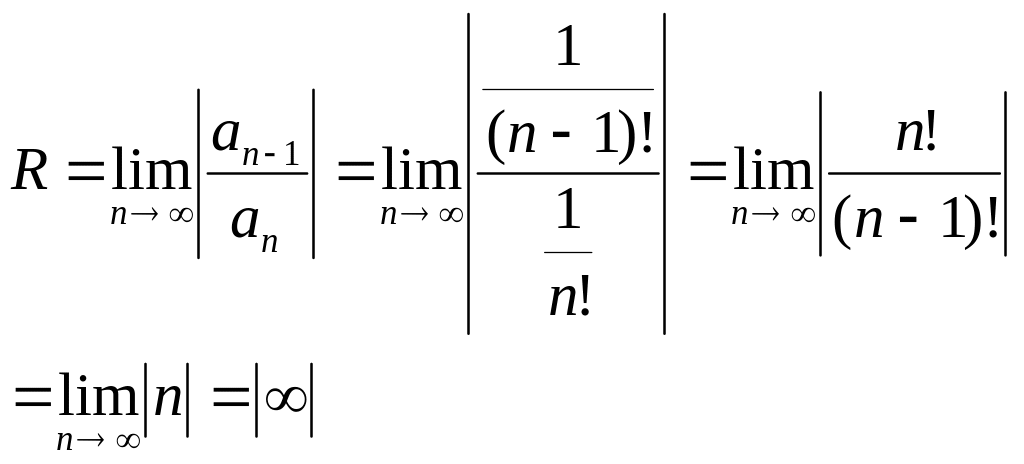 Следовательно,
данный ряд сходится при любом значении
х.
Общий член этого ряда стремится к нулю.
Следовательно,
данный ряд сходится при любом значении
х.
Общий член этого ряда стремится к нулю.![]()
![]()
![]() с вероятностью
с вероятностью
![]() . Обозначим
Ai
– наступление события А в испытании с
номером i.
Т.к. условия проведения опытов одинаковые,
то эти вероятности равны. Если в
результате п
опытов событие А наступает ровно т
раз, то остальные п-т
раз это событие не наступает. Событие
А может появиться т
раз в п
испытаниях в различных комбинациях,
число которых равно количеству сочетаний
из п
элементов по т.
Это количество сочетаний
находится по формуле
. Обозначим
Ai
– наступление события А в испытании с
номером i.
Т.к. условия проведения опытов одинаковые,
то эти вероятности равны. Если в
результате п
опытов событие А наступает ровно т
раз, то остальные п-т
раз это событие не наступает. Событие
А может появиться т
раз в п
испытаниях в различных комбинациях,
число которых равно количеству сочетаний
из п
элементов по т.
Это количество сочетаний
находится по формуле![]()
![]()
![]()
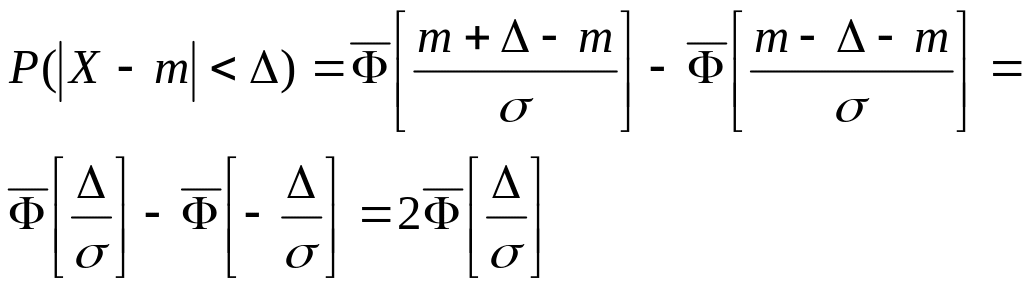 Если
принять
= 3,
то получаем с использованием таблиц
значений функции Лапласа:
Если
принять
= 3,
то получаем с использованием таблиц
значений функции Лапласа:![]() Т.е.
вероятность того, что случайная величина
отклонится от своего математического
ожидание на величину, большую чем
утроенное среднее квадратичное
отклонение, практически равна нулю.
Т.е.
вероятность того, что случайная величина
отклонится от своего математического
ожидание на величину, большую чем
утроенное среднее квадратичное
отклонение, практически равна нулю.
