Оценка чувствительности модели

Очевидно, что устойчивость является положительным свойством модели. Однако если изменение входных воздействий или параметров модели (в некотором заданном диапазоне) не отражается на значениях выходных параметров, то польза от такой модели невелика (ее можно назвать «бесчувственной»). В связи с этим возникает задача оценивания чувствительности модели к изменению параметров рабочей нагрузки и внутренних параметров самой системы.

19. Калибровка модели. Калибровка путем сравнения законов распределения вероятностей в модели и объекте.

Калибровка сравнением законов распределения вероятности. Адекватность может быть не обеспечена в модели вследствие того, что законы распределения, принятые в модели, не соответствуют законам, которые действуют на объекте. Калибровка модели по этому пункту ведётся в следующей последовательности. В модель закладывают законы распределения, по предположению, близкие к объекту или же изменяют модель таким образом, чтобы законы совпадали. Для того чтобы проверить насколько законы совпадают, используется критерий согласия (критерий согласия Пирсона).

Для проверки по степени совпадения (согласия) распределений проводятся следующие вычисления. Теоретическое определяется по таблице распределения при заданных значениях уровня доверия и степенях свободы V = m-2, где m – число групп ряда распределения, составляющих статистическую совокупность (группа близких значений). Фактическое определяют по формуле 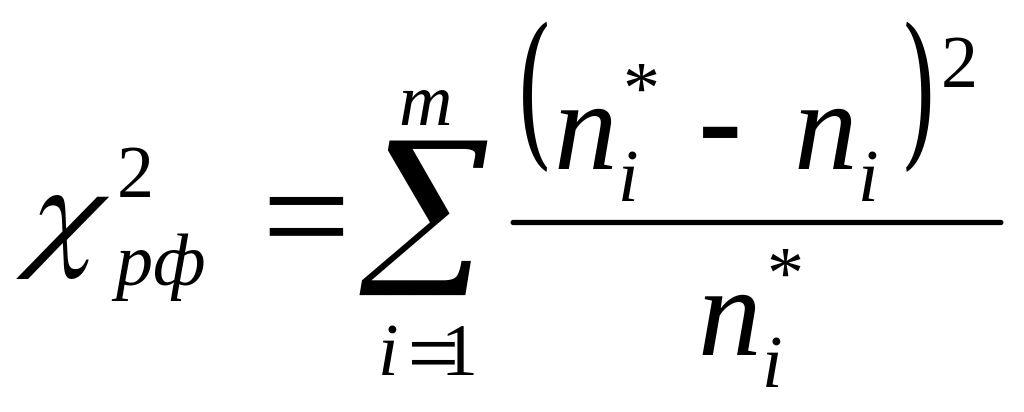, где и - частота попадания значений исследуемого параметра в i-ю группу соответственно в выбранном законе распределения и в теоретическом законе распределения (на объекте). Затем сравнивается с . Если окажется, что , то выбранные законы распределения в модели совпадают с законами на объекте. Если законы не совпадают, то в модели задаются другие совпадающие законы.

Далее при совпадающих законах распределения проверяется адекватность модели. Если модель не адекватна, переходят ко 2-ому этапу – балансировке.

20. Калибровка модели. Балансировка и оптимизация модели.

Калибровка балансировкой модели. Адекватность модели может быть не обеспечена из-за неправильно выбранной области значений параметров. Поэтому на этом этапе проводится поиск такой области значения по каждому из параметров, чтобы результаты совпадали. Выполняется это следующим образом. В модели и на объекте изменяется значение параметра р в широком диапазоне. При каждом значении параметра вычисляется сумма квадратов отклонения . Если найденная сумма квадратов S_р приняла минимальное допустимое значение, значит по параметру р осуществлена балансировка. Если баланс по какому-то параметру отсутствует, то путем изменения модели его добиваются. Далее проверяется адекватность сбалансированной модели. Если балансировка не даёт положительных результатов, переходят к оптимизации.

Калибровка оптимизацией модели. На этом этапе на основе корелляционно-регрессионного анализа (см. подпункт 5 пункта 6 раздела «Обработка результатов эксперимента») определяется параметр, который может искажать наибольшим образом структуру и состав модели (иметь сильную зависимость с большими значениями), например, p_i . Для его исключения модель перестраивается так, чтобы указанный параметр был незначительным, добиваясь при этом чтобы оценка значимости коэффициента а₁ в линейной регрессии S_pi = a₀ + a₁p_i , описывающей выходную функциональную зависимость модели, была минимальной. Если в результате изменения модели коэффициент а₁ становится незначимым, проводится проверка адекватности. Если модель и в этом случае окажется не адекватной, переходят к полной перестройке модели.