29. Направления выпуклости и точки перегиба.

Определение.

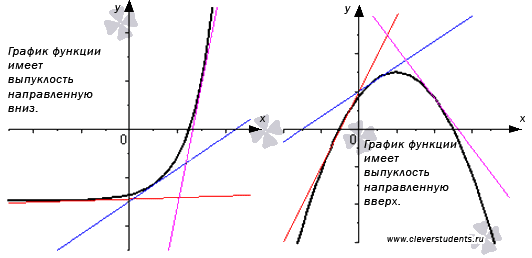
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Определение.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

30. Асимптоты. Вертикальная

Вертикальная асимптота — прямая вида   при условии существования предела  .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — прямая вида   при условии существования предела

.

Наклонная

Наклонная асимптота — прямая вида   при условии существования пределов

1. 

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен  ), то наклонной асимптоты при   (или  ) не существует.

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела  , то наклонная асимптота совпадает с горизонтальной.

Горизонтальная асимптота является частным случаем наклонной при  , из этого следует что

1. Функция не может иметь наклонную асимптоту одновременно с горизонтальной при  , аналогично для  , но так же возможен случай когда и вовсе нет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

31.Общая схема исследования функции

1.      Область определения

2.      Исследование функции на четность, нечетность и периодичность

Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство  , то  – четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство  , то  – нечетная функция; в противном случае,  – общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

3.      Нахождение точек пересечения графика функции с осями координат

Точки пересечения с осью ОХ:  , где   – решение уравнения  .

Точки пересечения с осью ОY:  .

4.      Нахождение промежутков знакопостоянства функции

Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е.   или  .

5.      Нахождение производной функции, области определения производной, критических точек

Критические точки функции – внутренние точки области определения функции, в которых производная не существует или равна нулю.

6.      Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов

Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.

7.      Нахождение промежутков выпуклости функции и точек перегиба

Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.

8.      Исследование поведения функции на бесконечности и в окрестности точек разрыва

Для исследования поведения функции в окрестности точки разрыва   необходимо вычислить односторонние пределы:   и   . Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая   – вертикальная асимптота.

При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при   и  . Для этого нужно вычислить следующие пределы:  и   . Если оба предела существуют, то   – уравнение наклонной асимптоты при  . Частный случай наклонной асимптоты при   – горизонтальная асимптота.  Аналогично ищется наклонная асимптота при  . 

9.      Построение графика (при необходимости нужно найти значения функции в дополнительных точках)