Достаточные условия возрастания и убывания функции.

Достаточное условие возрастания и убывания функции.

   Теорема. 1) Если функция f(x), имеющая производную наотрезке [a, b], возрастает на этом отрезке, то ее производная на отрезке [a, b] не отрицательна, т. e. f' (x) ≥ 0.

2) Если функция f(x) непрерывна на отрезке [а, b] и диффе­ренцируема в промежутке (a, b), причём f' (x) > 0 для a < x <b, то эта функция возрастает на отрезке [а, b].

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

• найти область определения функции;

• найти производную функции;

• решить неравенства 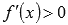  и   на области определения;

• к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

25.Экстремумы функции. Необходимое и достаточное условие экстремума.

Определение 1. Точка   называется точкой максимума [точкой минимума] функции  , если существует такая  - окрестность   точки  , что для всех значений   из этой окрестности выполняется неравенство    .

Определение 2. Значение функции в точке максимума (точке минимума) называетсямаксимумом (минимумом) функции  .

Определение 3. Точки минимума и точки максимума называются точками экстремумафункции  , а значения функции в этих точках — экстремумами функции  .

Теорема 1. Если функция   непрерывна в точке  , а   на промежутке   и   на промежутке  , то   является точкой максимума функции  .

Теорема 2. Если функция   непрерывна в точке  , а   на промежутке   и   на промежутке  , то   — точка минимума функции  .

Теорема 3 (Ферма). Пусть функция   определена в некоторой окрестности точки   и дифференцируема в этой точке. Если   — точка экстремума функции  , то  .

Теорема 4. Пусть функция   дифференцируема в некоторой окрестности точки  , кроме, быть может, самой точки  , и непрерывна в точке  . Тогда, если   меняет знак с « » на « » (с « » на « ») при переходе через точку  , то   — точка минимума (точка максимума) функции  .

26.Достаточное условие экстремума функции по второй производной.

Теорема

(Второе достаточное условие экстремума)

Пусть для функции   выполнены следующие условия:

она непрерывна в окрестности точки  ;

первая производная   в точке  ;

 в точке   .

Тогда в точке   достигается экстремум, причем, если  , то в точке   функция   имеет минимум; если , то в точке   функция   достигает максимум.

27.Исследование поведения функции в точке с помощью производных высшего порядка

3. 

28.Наибольшее и наименьшее значение функции на отрезке

Наибольшим значением функции y=f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  .

Если функция   определена и непрерывна на отрезке   , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение   функция   принимает в точке  , то  будет локальным максимумом функции  , так как в этом случае существует окрестность точки  , такая, что   .

Однако свое наибольшее значение   функция   может принимать и на концах отрезка   . Поэтому, чтобы найти наибольшее значение   непрерывной на отрезке   функции  , надо найти все максимумы функции на интервале   и значения   на концах отрезка  , то есть   и  , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.

Наименьшим значением   непрерывной на отрезке   функции   будет наименьший минимум среди всех минимумов функции   на интервале   и значений   и  .