
- •1.Предел функции в точке. Ограниченность функции, имеющей конечный предел.
- •2. Единственность предела функции (док-во).
- •3.Бесконечно малые функции и их свойства.
- •4.Теорема о связи функции, имеющей предел и бесконечно малой функций. Арифметические свойства пределов функций (одно с док-ном).
- •5. Бесконечно малые и бесконечно большие функции. Связь между ними.
- •Бесконечно малая
- •Бесконечно большая
- •6. Сравнение бесконечно малых функций. Эквивалентные функции. Свойства эквивалентных функций. Условие эквивалентности.
- •Эквивалентность
- •7.Теорема о замене функций на эквивалентные при вычислении пределов.
- •8.Непрерывность функции в точке. Теорема о непрерывности сложной функции. Точки разрыва. Их классификация.
- •9.Свойства функций, непрерывных на отрезке.
- •10Производная. Её геометрический и механический смысл. Уравнение касательной и нормали к графику функции.
- •11Правила дифференцирования.
- •12Понятие дифференцируемой функции. Необходимое и достаточное условие дифференцируемости (док-во).
- •13.Дифференциал функции. И его геометрический смысл.
- •14.Производная сложной функции. Логарифмическое дифференцирование.
- •15.Теорема о существовании обратной функции. Производная обратной функции
- •16.Таблица производных. Вывод производной одной из функций.
- •17.Производные и дифференциалы высшего порядка. Инвариантность формы первого дифференциала.
- •18.Теорема Ролля. Её геометрический смысл.
- •19.Теорема Коши (с док-вом). Теорема Лагранжа (без док-ва). Геометрический смысл.
- •20.Правило Лопиталя.
- •21.Формула Тейлора с остаточным членом в форме Лагранжа.
- •22.Формула Тейлора с остаточным членом в Пеано.
- •23.Разложение элементарных функций по формуле Тейлора.
- •24.Необходимое и достаточное условие монотонности функции. Возрастание и убывание функции в точке и на отрезке. Условие возрастания (убывания) в точке.
- •Достаточные условия возрастания и убывания функции.
- •25.Экстремумы функции. Необходимое и достаточное условие экстремума.
- •26.Достаточное условие экстремума функции по второй производной.
- •27.Исследование поведения функции в точке с помощью производных высшего порядка
- •28.Наибольшее и наименьшее значение функции на отрезке
- •29. Направления выпуклости и точки перегиба.
- •30. Асимптоты. Вертикальная
- •Горизонтальная
- •Наклонная
- •Связь между наклонной и горизонтальной асимптотами
- •31.Общая схема исследования функции
21.Формула Тейлора с остаточным членом в форме Лагранжа.
22.Формула Тейлора с остаточным членом в Пеано.
Формула Тейлора с остаточным членом в форме Пеано.
Рассмотрим
произвольный многочлен степени
 :
:
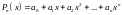 .
.
Где
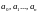 - постоянные числа, коэффициенты
многочлена.
- постоянные числа, коэффициенты
многочлена.
Найдем
последовательные производные и вычислим
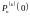 :
:
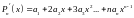 ,
,
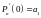
 ,
,
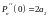
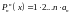
Т.е.
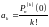 ,
(
,
(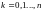 ),
где мы считаем, что
),
где мы считаем, что
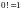 ,
,
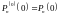 .
.
Тогда получим многочлен Тейлора:
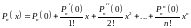
Если
надо представить многочлен вида:
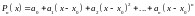 .
Где
.
Где
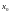 - любое фиксированное число. Проделав
аналогичную процедуру получим:
- любое фиксированное число. Проделав
аналогичную процедуру получим:
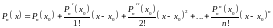 -
формула Тейлора для многочлена
-
формула Тейлора для многочлена
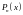 по степеням
по степеням
 .
.
Любую
функцию можно представить в виде
многочлена:
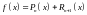 .
Где
- многочлен Тейлора, а
.
Где
- многочлен Тейлора, а
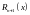 - остаточный член. Т.е.:
- остаточный член. Т.е.:
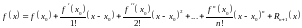 ,
если
мало, то
,
если
мало, то
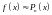 .
.
Остаточный
член в форме Лагранжа:
 ,
,
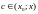 .
.
Замечание: остаточный член мал, как правило, можно пренебречь по сравнению с предыдущим слагаемым.
Рассмотрим
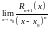 и
и
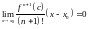 ,
следовательно
,
следовательно
 ,
называется б/м более высокого порядка
чем
,
называется б/м более высокого порядка
чем
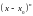 ,
т.е.
,
т.е.
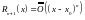 - остаточный член в форме Пеано.
- остаточный член в форме Пеано.
Замечание: если взять минимальное число членов формулы Тейлора, то получатся формулы асимптотического разложения.
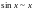 ,
,
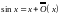
Формула
Тейлора даёт более точное разложение:
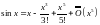
23.Разложение элементарных функций по формуле Тейлора.
Представление некоторых функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений.
Рассмотрим
частный случай
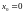 (Формула
Маклорена):
(Формула
Маклорена):
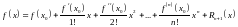 .
.
1)
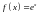 ,
,

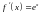 ,
,
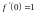
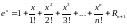 .
.
2)
 ,
,
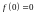
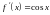 ,
,
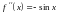 ,
,
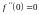
 ,
,
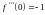
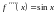 ,
,
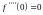
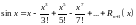 .
.
3)
 ,
,
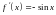 ,
,

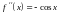 ,
,
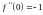
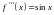 ,
,
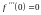
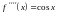 ,
,
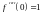
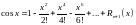 .
.
4)
 ,
,
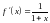 ,
,
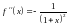 ,
,
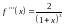 ,
,

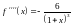 ,
,
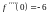
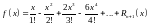 или
или
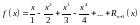 .
.
5)
 ,
,
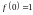
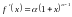 ,
,
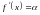
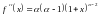 ,
,
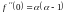
 ,
,
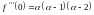
24.Необходимое и достаточное условие монотонности функции. Возрастание и убывание функции в точке и на отрезке. Условие возрастания (убывания) в точке.
Теорема (критерий возрастания и убывания функции на интервале)
Для
того чтобы дифференцируемая
функция
на
интервале ![]() была
возрастающая,
необходимо и достаточно, чтобы
была
возрастающая,
необходимо и достаточно, чтобы ![]() была
неотрицательна для любого
значения
была
неотрицательна для любого
значения ![]() из интервала
.
Доказательство
из интервала
.
Доказательство
Необходимость
Дано: возрастает на интервале .
Требуется доказать:
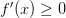 .
.
Пусть ![]() произвольная
точка на интервале
,
пусть
произвольная
точка на интервале
,
пусть ![]() ,
тогда
в силу монотонного возрастания
функфии
,
тогда
в силу монотонного возрастания
функфии ![]() для
любого значения
из интервала
,
для
любого значения
из интервала
,![]() ,
,![]()
![]()
По свойству сохранения знака предела:
![]()
а
это и есть![]() .
.
Достаточность
Дано: .
Требуется доказать: возрастает на интервале .
Пусть
для
любого значения
из интервала
.
Выберем
произвольные точки ![]() и
и ![]() ,
принадлежащие интервалу
,
и
применим к функции
,
принадлежащие интервалу
,
и
применим к функции ![]() на формулу
Лагранжа о
конечных приращениях:
на формулу
Лагранжа о
конечных приращениях:
![]() Из
того что
Из
того что ![]() Доказали
нестрогое возрастание.
Доказали
нестрогое возрастание.
Теорема (достаточное условие строгой монотонности)
Если для любых значений из
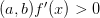 ,то
строго
возрастает на
,то
строго
возрастает на 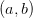 .
.Если для любых значений из
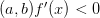 ,то
строго
убывает на
.
,то
строго
убывает на
.
Доказательство
Пусть ![]() ,
применим формулу
конечных приращений Лагранжа:
,
применим формулу
конечных приращений Лагранжа: ![]() так
как
и
так
как
и ![]() ,
то
,
то ![]() .
Пусть
.
Пусть ![]() ,
применим формулу
конечных приращений Лагранжа:
,
применим формулу
конечных приращений Лагранжа: ![]() так
как
и
,
то
.
так
как
и
,
то
.
Пример
Исследовать
функцию ![]() на
возрастание и убывание.
на
возрастание и убывание.
Решение
Функция
имеет производную ![]() в
любой точке интервала
в
любой точке интервала ![]() .Для
определения промежутков возрастания
и убывания функции решаем
неравенства:
.Для
определения промежутков возрастания
и убывания функции решаем
неравенства: ![]() и
и ![]() Точки,
в которых производная равна
нулю, то есть
Точки,
в которых производная равна
нулю, то есть ![]() и
и ![]() ,
разобьютчисловую
прямую на
три интервала.
Получаем:
,
разобьютчисловую
прямую на
три интервала.
Получаем:
![]() возрастает
на отрезках
возрастает
на отрезках ![]()
![]() убывает
на отрезке
убывает
на отрезке ![]() .
Для проверки построим график этой
функции.
.
Для проверки построим график этой
функции.
Ответ:
возрастает
на отрезках ![]() и
и ![]() .
убывает
на отрезке
.
Возрастание
и убывание
функции,
функция y = f (x)
называется возрастающей на отрезке
[a, b], если
для любой пары точек х и х', а
£ х < х' £ bвыполняется
неравенство f (x) £
f (x'),
и строго возрастающей — если выполняется
неравенство f (x)
< f (x').
Аналогично определяется убывание и
строгое убывание функции. Например,
функция у = х2 (рис.,
а) строго возрастает на отрезке [0,1], а
.
убывает
на отрезке
.
Возрастание
и убывание
функции,
функция y = f (x)
называется возрастающей на отрезке
[a, b], если
для любой пары точек х и х', а
£ х < х' £ bвыполняется
неравенство f (x) £
f (x'),
и строго возрастающей — если выполняется
неравенство f (x)
< f (x').
Аналогично определяется убывание и
строгое убывание функции. Например,
функция у = х2 (рис.,
а) строго возрастает на отрезке [0,1], а
![]()
(рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x), а убывающие f (x)¯. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].
Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x0, если найдётся такой интервал (a, b), содержащий точку x0, что для любой точки х из (a, b), х> x0, выполняется неравенство f (x0)£ f (x), и для любой точки х из (a, b), х< x0, выполняется неравенство f (x) £ f(x0). Аналогично определяется строгое возрастание функции в точке x0. Еслиf'(x0) > 0, то функция f (x) строго возрастает в точке x0. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.



