
- •1.Предел функции в точке. Ограниченность функции, имеющей конечный предел.
- •2. Единственность предела функции (док-во).
- •3.Бесконечно малые функции и их свойства.
- •4.Теорема о связи функции, имеющей предел и бесконечно малой функций. Арифметические свойства пределов функций (одно с док-ном).
- •5. Бесконечно малые и бесконечно большие функции. Связь между ними.
- •Бесконечно малая
- •Бесконечно большая
- •6. Сравнение бесконечно малых функций. Эквивалентные функции. Свойства эквивалентных функций. Условие эквивалентности.
- •Эквивалентность
- •7.Теорема о замене функций на эквивалентные при вычислении пределов.
- •8.Непрерывность функции в точке. Теорема о непрерывности сложной функции. Точки разрыва. Их классификация.
- •9.Свойства функций, непрерывных на отрезке.
- •10Производная. Её геометрический и механический смысл. Уравнение касательной и нормали к графику функции.
- •11Правила дифференцирования.
- •12Понятие дифференцируемой функции. Необходимое и достаточное условие дифференцируемости (док-во).
- •13.Дифференциал функции. И его геометрический смысл.
- •14.Производная сложной функции. Логарифмическое дифференцирование.
- •15.Теорема о существовании обратной функции. Производная обратной функции
- •16.Таблица производных. Вывод производной одной из функций.
- •17.Производные и дифференциалы высшего порядка. Инвариантность формы первого дифференциала.
- •18.Теорема Ролля. Её геометрический смысл.
- •19.Теорема Коши (с док-вом). Теорема Лагранжа (без док-ва). Геометрический смысл.
- •20.Правило Лопиталя.
- •21.Формула Тейлора с остаточным членом в форме Лагранжа.
- •22.Формула Тейлора с остаточным членом в Пеано.
- •23.Разложение элементарных функций по формуле Тейлора.
- •24.Необходимое и достаточное условие монотонности функции. Возрастание и убывание функции в точке и на отрезке. Условие возрастания (убывания) в точке.
- •Достаточные условия возрастания и убывания функции.
- •25.Экстремумы функции. Необходимое и достаточное условие экстремума.
- •26.Достаточное условие экстремума функции по второй производной.
- •27.Исследование поведения функции в точке с помощью производных высшего порядка
- •28.Наибольшее и наименьшее значение функции на отрезке
- •29. Направления выпуклости и точки перегиба.
- •30. Асимптоты. Вертикальная
- •Горизонтальная
- •Наклонная
- •Связь между наклонной и горизонтальной асимптотами
- •31.Общая схема исследования функции
17.Производные и дифференциалы высшего порядка. Инвариантность формы первого дифференциала.
18.Теорема Ролля. Её геометрический смысл.
Теорема
Ролля. Её
геометрический
смысл.Пусть
функция
непрерывна на отрезке
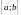 ,
дифференцируема хотя бы на отрезке
,
дифференцируема хотя бы на отрезке
 и значение функции на концах отрезка
совпадает, т.е.
и значение функции на концах отрезка
совпадает, т.е.
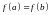 ,
тогда существует хотя бы одна точка
,
тогда существует хотя бы одна точка
 ,
т.ч.
,
т.ч.
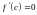 .
.
Доказательство.
1) Пусть наибольшее и наименьшее значения
функции
на отрезке
совпадают, т.е.
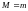 и функция
постоянна тогда
и функция
постоянна тогда
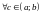 производная
.
2) Пусть функция непостоянна, тогда она
достигает на интервале
наибольшего и наименьшего значения.
Причем функция не может достигать
производная
.
2) Пусть функция непостоянна, тогда она
достигает на интервале
наибольшего и наименьшего значения.
Причем функция не может достигать
 и
и
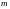 на концах отрезка, т.к.
и функция была бы постоянна. Значит,
внутри интервала
есть точка экстремума
на концах отрезка, т.к.
и функция была бы постоянна. Значит,
внутри интервала
есть точка экстремума
 ,
.
,
.
Геометрический
смысл.
Если все условия теоремы выполнены, то
на графике функции
существует точка
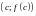 ,
через которую
проходит
касательная к графику функции, параллельно
оси x
,
через которую
проходит
касательная к графику функции, параллельно
оси x
19.Теорема Коши (с док-вом). Теорема Лагранжа (без док-ва). Геометрический смысл.
Теорема
Коши:
Пусть функция
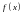 и
и
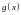 непрерывны
на отрезке
,
дифференцируемы хотя бы на отрезке
,
непрерывны
на отрезке
,
дифференцируемы хотя бы на отрезке
,
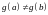 ,
тогда существует точка
,
т.е.
,
тогда существует точка
,
т.е.
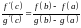
:
Пусть функция
непрерывна на отрезке
,
дифференцируема хотя бы на отрезке
,
тогда существует точка
,
т.ч.
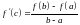 .
.
Доказательство.
Рассмотрим
вспомогательную функцию
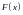 непрерывную на отрезке
,
дифференцируемую хотя бы на отрезке
:
непрерывную на отрезке
,
дифференцируемую хотя бы на отрезке
:
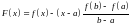 .
Тогда
.
Тогда
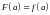 ,
а
,
а
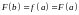 ,
т.е. выполнены все условия теоремы Ролля
и существует
,
т.ч.
,
т.е. выполнены все условия теоремы Ролля
и существует
,
т.ч.
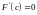 .
Следовательно,
.
Следовательно,
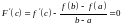 ,
.
,
.
Теорема Лагранжа) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b).
Тогда существует точка с О (a, b) такая, что
|
f(b) − f(a) = f '(c) · (b − a) . |
(1) |
Формула (1) называется формулой Лагранжа, или формулой конечных приращений
Из
теоремы Лагранжа следует формула
конечных приращений:
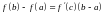 .
.
Геометрический
смысл.
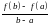 -
-
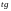 угла наклона секущей (хорды), стягивающей
точки
угла наклона секущей (хорды), стягивающей
точки
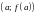 и
и
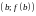 графика
.
графика
.
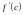 -
угла наклона касательной к графику
функции
,
через точку касания
.
Если все условия теоремы Лагранжа
выполнены, то касательная проходящая
через точку
,
параллельна секущей (хорде), точки
и
графика
.
-
угла наклона касательной к графику
функции
,
через точку касания
.
Если все условия теоремы Лагранжа
выполнены, то касательная проходящая
через точку
,
параллельна секущей (хорде), точки
и
графика
.
20.Правило Лопиталя.
Правило Лопиталя.
Правило Лопиталя для вычисления пределов.
Пусть
функции f(x)
и g(x)
определены и дифференцируемы в некоторой
проколотой окрестности точки а. Пусть
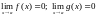 и
и
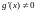 в указанной окрестности. Тогда, если
существует
в указанной окрестности. Тогда, если
существует
 ,
то существует
,
то существует
 и имеет место равенство
=
.
и имеет место равенство
=
.
Доказательство. Доопределим функции f(x) и g(x) при х=а: f(a)=0, g(a)=0. Тогда эти функции станут непрерывными в окрестности точки а.
Рассмотрим отрезок [а;х], если x>a и отрезок [x;a], если x<a, причём х принадлежит окрестности, о которой говориться в условии теоремы.
Для
функций f(x)
и g(x)
на указанных отрезках выполнены условия
теоремы Коши. Поэтому можно записать
![]()
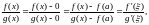 причём
причём
![]() .
Поэтому, если
.
Поэтому, если
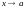 ,
то и
,
то и
![]() .
Так как по условию теоремы существует
,
то существует и
.
Так как по условию теоремы существует
,
то существует и
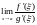 и эти пределы равны. Стало быть
=
=
.
и эти пределы равны. Стало быть
=
=
.
