
- •1.Предел функции в точке. Ограниченность функции, имеющей конечный предел.
- •2. Единственность предела функции (док-во).
- •3.Бесконечно малые функции и их свойства.
- •4.Теорема о связи функции, имеющей предел и бесконечно малой функций. Арифметические свойства пределов функций (одно с док-ном).
- •5. Бесконечно малые и бесконечно большие функции. Связь между ними.
- •Бесконечно малая
- •Бесконечно большая
- •6. Сравнение бесконечно малых функций. Эквивалентные функции. Свойства эквивалентных функций. Условие эквивалентности.
- •Эквивалентность
- •7.Теорема о замене функций на эквивалентные при вычислении пределов.
- •8.Непрерывность функции в точке. Теорема о непрерывности сложной функции. Точки разрыва. Их классификация.
- •9.Свойства функций, непрерывных на отрезке.
- •10Производная. Её геометрический и механический смысл. Уравнение касательной и нормали к графику функции.
- •11Правила дифференцирования.
- •12Понятие дифференцируемой функции. Необходимое и достаточное условие дифференцируемости (док-во).
- •13.Дифференциал функции. И его геометрический смысл.
- •14.Производная сложной функции. Логарифмическое дифференцирование.
- •15.Теорема о существовании обратной функции. Производная обратной функции
- •16.Таблица производных. Вывод производной одной из функций.
- •17.Производные и дифференциалы высшего порядка. Инвариантность формы первого дифференциала.
- •18.Теорема Ролля. Её геометрический смысл.
- •19.Теорема Коши (с док-вом). Теорема Лагранжа (без док-ва). Геометрический смысл.
- •20.Правило Лопиталя.
- •21.Формула Тейлора с остаточным членом в форме Лагранжа.
- •22.Формула Тейлора с остаточным членом в Пеано.
- •23.Разложение элементарных функций по формуле Тейлора.
- •24.Необходимое и достаточное условие монотонности функции. Возрастание и убывание функции в точке и на отрезке. Условие возрастания (убывания) в точке.
- •Достаточные условия возрастания и убывания функции.
- •25.Экстремумы функции. Необходимое и достаточное условие экстремума.
- •26.Достаточное условие экстремума функции по второй производной.
- •27.Исследование поведения функции в точке с помощью производных высшего порядка
- •28.Наибольшее и наименьшее значение функции на отрезке
- •29. Направления выпуклости и точки перегиба.
- •30. Асимптоты. Вертикальная
- •Горизонтальная
- •Наклонная
- •Связь между наклонной и горизонтальной асимптотами
- •31.Общая схема исследования функции
13.Дифференциал функции. И его геометрический смысл.
Дифференциалом функции называют главную часть приращения в точке х, соответствующим приращению аргумента х. Дифференциал dy=Ax=f’(x)x или dy=f’(x)dx.
Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0,f(x0)) при изменении x0 на величину x
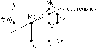
14.Производная сложной функции. Логарифмическое дифференцирование.
Производные и дифференциалы высших порядков.
I.
Производной 2-го порядка от функции
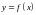 называется производная от ее первой
производной:
называется производная от ее первой
производной:
 .
Вообще, производной n-го
порядка называется производная от
производной порядка n-1:
.
Вообще, производной n-го
порядка называется производная от
производной порядка n-1:
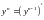 .
.
II.
Пусть функция
дифференцируема, тогда приращение
функции
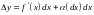 ,
следовательно
,
следовательно
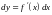 - дифференциал I-го
порядка.
- дифференциал I-го
порядка.
Рассмотрим
1-й
случай, когда x
– независимая переменная. Тогда
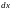 - число. Предполагая, что функция
дифференцируема дважды в т. x,
найдем дифференциал от дифференциала
I-го
порядка при
- число. Предполагая, что функция
дифференцируема дважды в т. x,
найдем дифференциал от дифференциала
I-го
порядка при
 :
:
 ,
,
 - полученное выражение при
называется дифференциалом II-го
порядка. Аналогично:
- полученное выражение при
называется дифференциалом II-го
порядка. Аналогично:
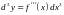 ,
,
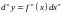 .
.
Рассмотрим
2-й
случай, когда
 ,
а
,
а
 - соответственно сложная функция. Тогда
- дифференциал I-го
порядка, а
- функция,
- соответственно сложная функция. Тогда
- дифференциал I-го
порядка, а
- функция,
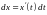 .
Тогда:
.
Тогда:
 ,
,
 ,
,
 ,
,
 .
Дифференциалы 2-го (и более высокого
порядка) не обладают инвариантностью
формы (т.е. меняют вид в зависимости
от x).
.
Дифференциалы 2-го (и более высокого
порядка) не обладают инвариантностью
формы (т.е. меняют вид в зависимости
от x).
15.Теорема о существовании обратной функции. Производная обратной функции
(док-во). Пример дифференцирования обратной функции.
Производная обратной функции. Производные обратных тригонометрических функций.
I.
Если
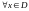 (D
– область определения) поставлен в
соответствие
(D
– область определения) поставлен в
соответствие
 ,
говорят, задана функция
.
Если это взаимно однозначно, то можно
рассмотреть функцию
,
говорят, задана функция
.
Если это взаимно однозначно, то можно
рассмотреть функцию
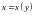 ,
которая
,
которая
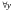 ставит в соответствие x.
ставит в соответствие x.
Теорема:
Пусть
 и
взаимно обратные функции, тогда
и
взаимно обратные функции, тогда
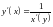 или
или
 .
Доказательство. Пусть обе функции
дифференцируемы в некоторой точке.
Тогда,
.
Доказательство. Пусть обе функции
дифференцируемы в некоторой точке.
Тогда,
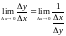 ,
т.к. обе функции дифференцируемы
,
т.к. обе функции дифференцируемы
 непрерывны, т.е.
непрерывны, т.е.
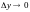 при
при
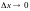 .
Тогда,
.
Тогда,
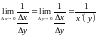 .
.
а)
 ,
,
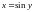 ,
тогда
,
тогда
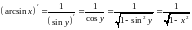 ,
,
б)
 ,
,
 ,
,
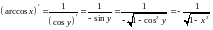 ,
,
в)
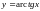 ,
,
 ,
,
 ,
,
г)
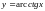 ,
,
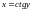 ,
,
 .
.
16.Таблица производных. Вывод производной одной из функций.
Таблица производных простейших элементарных функций
Легко получить следующую таблицу производных основных элементарных функций, используя определение производной. Для более подробного изучения данного материала рекомендуем использовать, например, "Математический анализ" ч.1 В.А. Ильина, В.А. Садовничего, Бл.Х. Сендова.
(ua(x))' = a ua-1(x)u'(x), в частности,
(1/u(x))'
= -u'(x)/u2(x),
(![]() )'
= u'(x)/2
;
)'
= u'(x)/2
;
(logau(x))' = (u'(x)logae)/u(x) при 0<a№1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x);
(au(x))' = au(x)ln a u'(x) при 0<a№1, в частности, (eu(x))' = u'(x)eu(x);
(sin u(x))' = cos u(x)u'(x);
(cos u(x))' = -sin u(x)u'(x);
(tg u(x))' = u'(x)/cos2u(x) x№ p/2+p n, n=0,+-1,...;
(ctg u(x))' = -u'(x)/sin2u(x) x№ p n, n=0,+-1,...;
(arcsin u(x))' = u'(x)/
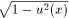 ,
-1<u(x)<1;
,
-1<u(x)<1;(arccos u(x))' = -u'(x)/ , -1<u(x)<1;
(arctg u(x))' = u'(x)/(1+u2(x));
(arcctg u(x))' = -u'(x)/(1+u2(x)).
Введем гиперболические функции:
sh x = (1/2)(ex-e-x)- гиперболический синус;
ch x = (1/2)(ex+ex)- гиперболический косинус;
th x = sh x/ch x -гиперболический тангенс;
cth x = ch x/sh x - гиперболический котангенс.
Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных.
(sh x)' = ch x;
(ch x)' = sh x;
(th x)' = 1/ch2 x;
(cth x)' = -1/sh2 x.
Пример 7. Найти y', если
y(x) = x3arcsin x.
![]()
y(x) = ln sin (x2+1).
y' = (2xcos(x2+1))/sin(x2+1) = 2x ctg(x2+1)
Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций.
