Билеты «математический анализ»

1.Предел функции в точке. Ограниченность функции, имеющей конечный предел.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Рассмотрим функцию , определённую на некотором множестве , которое имеет предельную точку (которая, в свою очередь, не обязана ему принадлежать).

Предел функции по Гейне Значение называется пределом (предельным значением) функции в точке , если для любой последовательности точек , сходящейся к , но не содержащей в качестве одного из своих элементов (то есть в проколотой окрестности ), последовательность значений функции сходится к .

Предел функции по Коши Значение называется пределом (предельным значением) функции в точке , если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов , удовлетворяющих условию , выполняется неравенство

Ограниченность: Теорема. Если f(х) имеет конечный предел в т.Х₀ , то существует выколотая окрестность этой точки, такая, что f(x) ограничена в этой окрестности.

2. Единственность предела функции (док-во).

Формулировка:

Если функция   в точке   имеет предел, то этот предел единственный.

Доказательство:

Докажем методом от противного. Предположим, что  ,  ,  . Возьмём  , по определению и свойству окрестности найдётся такая проколотая   -окрестность точки   ( ), в которой одновременно будут выполнятся неравенства  ,   , тогда в точках этой же окрестности  . Получили противоречие  . Отсюда, функция   в точке   имеет единственный предел.

3.Бесконечно малые функции и их свойства.

Бесконечно малая

Последовательность   называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  .

Свойства бесконечно малых

• Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если   — бесконечно малая последовательность, сохраняющая знак, то 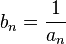  — бесконечно большая последовательность.

4.Теорема о связи функции, имеющей предел и бесконечно малой функций. Арифметические свойства пределов функций (одно с док-ном).

Теоремы о предельном переходе в равенстве и неравенстве. Теорема о связи функции,имеющей предел и бесконечно малой функции:Для того,чтобы число А являлось пределом функции f(x) в т.Хо,необходимо и достаточно,чтобы функция f(x) представлялась в виде f(x)=A+α((x),где α(х)-бесконечно малая в точке Хо.

Арифметичкеские свойства пределов функции:

Т1:Если функции f(x) и g(x) имеют предел в точке Хо то f(x)+-g(x) имеют предел в точке, при этом:

Lim(f(x)+-g(x))=lim(f(x))+-lim(g(x)) Док-во: Lim(f(X)=A, f(x)=A+α(x)

Lim g(x)=B, g(x)=B+β(x) , где α(x), β(x)-б/м в т.Xo.

f(x)+g(x)=A+B+ β(x)+ α(x)

f(x)+g(x)=A+B+γ(x)=> γ(x)-б/м в т.Xo.

Lim( f(x)+g(x))=lim(f(x))+lim(g(x))=A+B. Т2:Если f(x),g(x) имеют пределы в т.Хо,то f(x)*g(x) имеет предел в этой точке

Lim[f(x)*g(x)]=lim f(x)*lim g(x) Т3: Если существует предел функций f(x),g(x) в точке Хо и g(x) ≠0,то существует предел функциb f(x)/g(x),причем lim f(x)/g(x) = lim(f(x))/lim(g(x)).

Теорема о предельном переходе в равенстве: Если в некоторой окрестности точки Xo значения функций g(x) и f(x) совпадают, то пределы этич функций в точке Хо равны (f(x)=g(x),lim f(x)= lim g(x)).

Теорема о предельном переходе в неравенстве: Если в некоторой окрестности точки Хо значение функции f(X) не превосходит соответственное значение g(x),то предел f(x) в т.Хо не превосходит предел g(x) в т.Хо f(x)≤g(x)=> lim f(x)≤lim g(x)