3. Визначений інтеграл

Розглянемо неперервну функцію на відрізку . Розіб’ємо цей відрізок довільним чином на n окремих відрізків завдовжки та виберемо в кожному з них, також довільним чином, по одній точці , визначимо в цих точках значення функції , а саме . Тепер розглянемо суму , яку називають інтегральною сумою, та її границю за умови, що і довжина найбільшого окремого відрізка прямує до нуля. Оскільки розбиття відрізка виконується довільним чином, то таких інтегральних сум, які мають одну спільну границю, можна скласти безліч.

Спільна границя всіх інтегральних сум функції на відрізку називається визначеним інтегралом від в границях від а до b та позначається .

З опису складання інтегральної суми, зазначеного вище, випливає, що вона відповідає приблизному значенню площі криволінійної трапеції, що утворена кривою та прямими .

Отже, визначений інтеграл за своїм змістом є числом, яке відповідає площі криволінійної трапеції, утвореній функцією на відрізку .

Визначений інтеграл має такі властивості.

1. При зміні границь інтегрування змінюється знак визначеного інтеграла, а саме:

.

2. Інтеграл з рівними границями дорівнює нулю, тобто

.

3. Відрізок інтегрування можна розбивати на частини, тобто

.

4. Інтеграл від суми функцій дорівнює сумі інтегралів від її доданків, тобто

.

5. Сталий множник виноситься за знак інтеграла, тобто

.

6. Визначений інтеграл дорівнює різниці значень невизначеного інтеграла при верхній та нижній границях його інтегрування (формула Ньютона – Лейбніца), тобто

.

Зазначимо, що властивості за позиціями 4 та 5 збігаються із відповідними властивостями невизначеного інтеграла. Розрахунок визначеного інтеграла базується на розглянутих в п. 5.2 способах визначення невизначеного інтеграла та зазначених вище властивостей визначеного інтеграла. Якщо для визначення невизначеного інтеграла застосовується спосіб заміни змінної , то за цією функціональною залежністю змінних необхідно і визначити нові границі інтегрування визначеного інтеграла, які відповідають змінній .

Визначений інтеграл має широке застосування в усіх галузях знань особи, яка приймає рішення (ОПР). Особливо тоді, коли будь-яке природне явище, за суб’єктивним баченням ОПР може подаватись як границя суми значень неперервної функції (функцій) на скінченному інтервалі.

5.4. Варіанти контрольних робіт

За 5.n.1. та 5.n.2 пропонується визначити невизначений інтеграл, за 5.n.3 та 5.n.4 пропонується обчислити визначений інтеграл.

5.1.1. ; 5.1.2. ;

5.1.3. ; 5.1.4. .

5.2.1. ; 5.2.2. ;

5.2.3. ; 5.2.4. .

5.3.1. ; 5.3.2. ;

5.3.3. ; 5.3.4. .

5.4.1. ; 5.4.2. ;

5.4.3. ; 5.4.4. .

5.5.1. ; 5.5.2. ;

5.5.3. ; 5.5.4. .

5.6.1. ; 5.6.2. ;

5.6.3. ; 5.6.4. .

5.7.1. ; 5.7.2. ;

5.7.3. ; 5.7.4. .

5.8.1. ; 5.8.2. ;

5.8.3. ; 5.8.4. .

5.9.1. ; 5.9.2. ;

5.9.3. ; 5.9.4. .

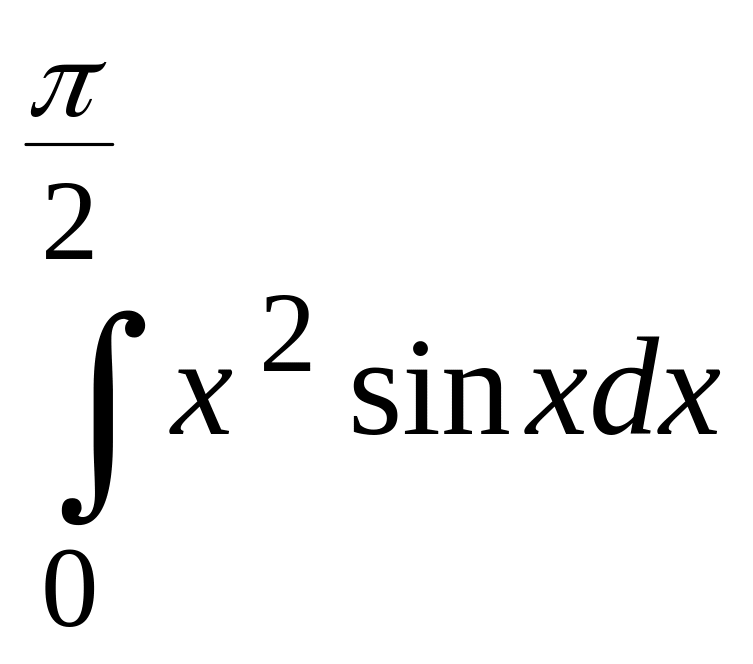5.10.1. ; 5.10.2. ;

5.10.3. ; 5.10.4. .

5.11.1. ; 5.11.2. ;

5.11.3. ; 5.11.4. .

5.12.1. ; 5.12.2. ;

5.12.3. ; 5.12.4. .

5.13.1. ; 5.13.2. ;

5.13.3. ; 5.13.4. .

5.14.1. ; 5.14.2. ;

5.14.3. ; 5.14.4. .

5.15.1. ; 5.15.2. ;

5.15.3. ; 5.15.4. .

5.16.1. ; 5.16.2. ;

5.16.3. ; 5.16.4.

5.17.1 . ; 5.17.2. ;

5.17.3. ; 5.17.4. .

5.18.1. ; 5.18.2.

5.18.3. ; 5.18.4. .

5.19.1. ; 5.19.2. ;

5.19.3. ; 5.19.4. .

5.20.1 ; 5.20.2. ;

5.20.3. ; 5.20.4. .

Примечания:

В этом разделе решать только первые два задания (например -5.х.1, 5.х.2, где х-вариант)

87