Сети ica

ICA (Independent Component Analysis, анализ независимых компонентов) также являются самоорганизующимися сетями на основе корреляции. Они используются обычно для обработки сигналов в режиме реального времени; исходно они разрабатывались для задачи так называемой слепой сепарации сигналов.

Задача, решаемая сетью – получить приближения сигналов s_j(t) в ситуации, когда известны только сигналы x_i(t), каждый из которых является линейной суперпозицией сигналов s_j(t): , причем коэффициенты a_ij также неизвестны. Исходные сигналы считаются статистически независимыми: один не несет никакой информации о другом.

Существует рекуррентная схема сети, с зависимостью выходного сигнала нейрона от выходных сигналов других нейронов:

Для такой сети применяется обучение по формуле, представляющей собой нелинейное обобщение правила Хебба:

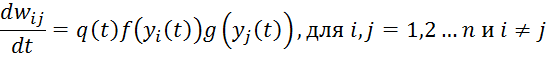
Параметрами обучения является скорость q(t), обычно убывающая до нуля в процессе обучения, а также нечетные функции f(y) и g(y), f(y)≠g(y). Обычно одна выпуклая, а другая вогнутая. Есть также модификации этой формулы, ускоряющие сходимость.

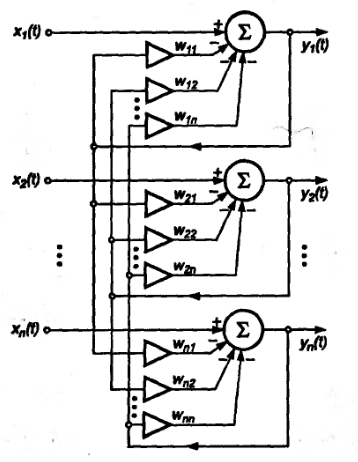
Рис. 1.5. Схема сети для разделения сигналов

Второй вариант – использование однонаправленных сетей.

Рис. 1.6. Схема однонаправленной сети разделения сигналов

В этой сети выходной сигнал нейрона формируется только из входных сигналов сети. Изменение весов производится по формуле Чихотского, либо одной из ее модифицированных версий.

Формула представлена в матричной форме, W – матрица весов.

Сети с самоорганизацией на основе конкуренции

Простейшая самоорганизующаяся сеть на основе конкуренции однослойна, все входные данные подаются на вход всем нейронам, таким образом, если входные данные имеют размерность N, у каждого нейрона есть N-мерный вектор связей. Победителем конкурентной борьбы при подаче на вход вектора x становится нейрон, чьи веса (после нормализации) наиболее близки к значениям компонент этого вектора. Для сравнения используются метрики расстояния между векторами, например евклидова мера:

Победитель, а также нейроны в его окрестности, обучаются по правилу Кохонена:

Здесь

S_w^(k) – окрестность на итерации k;

q_i^(k) – скорость обучения нейрона i на итерации k;

w_i – вектор весов нейрона i.

Размеры окрестности уменьшаются в процессе обучения. В процессе обучения веса нейронов в векторном пространстве сближаются, если нейроны реагируют на близкие векторы. Равенство w_i=w_j наступает тогда и только тогда, когда подаваемые этим нейронам векторы x_i и x_j совпадают или практически совпадают.

Для конкурентной борьбы характерной проблемой является слишком большой отрыв нейронов, уже становившихся победителями, и появление «мертвых» нейронов в областях, где недостаточная плотность обучающих векторов: такие нейроны имеют мало шансов на победу и их веса никогда не будут изменены. Для борьбы с этим используется механизм «утомления». Нейронам присваиваются потенциалы p_i, и после победы нейрона его собственный потенциал уменьшается, а потенциалы окружающих возрастают. Если потенциал нейрона опустился ниже порогового значения, он не принимает участия в конкурентной борьбе, пока его потенциал снова не восстановится.