
- •Задание № 6
- •Образец решения
- •Длина .
- •Длина .
- •5Кривые второго порядка на плоскости
- •Задание № 7
- •Образец выполнения задания
- •6Аналитическая геометрия в пространстве
- •Задание № 8
- •Задание № 9
- •7Комплексные числа и действия над ними
- •Показательная форма комплексного числа
- •Задание n 10
- •Задание № 11
- •Задание № 12
- •8Функция. Предел функции
- •Задание n 13
- •Задание № 14
- •9Производная функции
- •1. Основные формулы дифференцирования (таблица производных)
- •Правила дифференцирования
Плоскость в декартовой прямоугольной системе координат 0xyz может быть задана уравнением одного из следующих видов:
 - общее уравнение
плоскости;
- общее уравнение
плоскости; - уравнение
плоскости, проходящей через точку
- уравнение
плоскости, проходящей через точку
 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору
 ;
; - уравнение
плоскости в отрезках, где а,
b,
с
- величины направленных отрезков,
отсекаемых плоскостью на координатных
осях 0х,
0у,
0z
соответственно.
- уравнение
плоскости в отрезках, где а,
b,
с
- величины направленных отрезков,
отсекаемых плоскостью на координатных
осях 0х,
0у,
0z
соответственно.Пример
Написать уравнение плоскости, проходящей через точки
 и
и
 параллельно вектору
параллельно вектору
 .
.Решение
Задача имеет единственное решение, т.к. векторы
 и
неколлинеарны. В качестве нормального
вектора
и
неколлинеарны. В качестве нормального
вектора
 можно взять
можно взять .
.Уравнение плоскости имеет вид
 .
.Его можно преобразовать к виду
 .
.Прямая в пространстве может быть задана:
1) общими уравнениями

где коэффициенты
 ,
,
 ,
,
 не пропорциональны коэффициентам
не пропорциональны коэффициентам
 ,
,
 ,
,
 ,
что равносильно заданию прямой как
линии пересечения плоскостей;
,
что равносильно заданию прямой как
линии пересечения плоскостей;2) каноническими уравнениями
 ,
,что равносильно описанию прямой как линии пересечения трех плоскостей, проектирующих эту прямую на координатные плоскости. Здесь
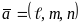 - направляющий вектор прямой, а точка
- направляющий вектор прямой, а точка
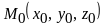 - некоторая точка, принадлежащая прямой;
- некоторая точка, принадлежащая прямой;3) параметрическими уравнениями

Параметрические уравнения получаются из канонических при выражении текущих координат x, y, z через параметр t;
4) уравнения прямой, проходящей через две заданные точки
 и
и

 .
.Пример
Прямая задана общими уравнениями

Написать ее канонические и параметрические уравнения.
Решение
В качестве направляющего вектора прямой может быть взят вектор
 ,
где
,
где
 ,
,
 - направляющие векторы плоскостей
- направляющие векторы плоскостей ,
,чтобы найти координаты точки
 придаем значение
придаем значение
 и подставляем в уравнения для плоскостей
и подставляем в уравнения для плоскостей
Решаем систему:
 ;
;  .
.Таким образом,
 .
.Канонические уравнения имеют вид:
 .
.Выражая x, y, z через t, получаем параметрические уравнения прямой:

Задание № 8
Написать уравнение плоскости, проходящей через точки
 и
и
 ,
параллельно вектору
,
параллельно вектору
 :
:1)

 2)
2)

 3)
3)


4)

 5)
5)

 6)
6)

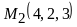
7)

 8)
8)

 9)
9)


10)

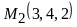 11)
11)

 12)
12)
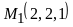

13)

 14)
14)

 15)
15)

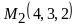
16)

 17)
17)

 18)
18)


19)

 20)
20)
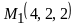
 .
.Задание № 9
Написать канонические и параметрические уравнения прямой заданной общими уравнениями
1)
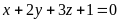 ;
;
 2)
2)
 ;
;
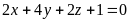
3)
 ;
;
 4)
4)
 ;
;
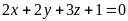
5)
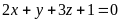 ;
;
 6)
6)
 ;
;
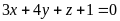
7)
 ;
;
 8)
8)
 ;
;

9)
 ;
;
 10)
10)
 ;
;

11)
 ;
;
 12)
12)
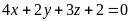 ;
;

13)
 ;
;
 14)
14)
 ;
;

15)
 ;
;
 16)
16)
 ;
;

17)
 ;
;
 18)
18)
 ;
;
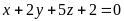
19)
 ;
;
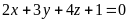 20)
20)
 ;
;

