38.Критерий устойчивости Найквиста.

Амплитудно-фазовый критерий Найквиста служит для определения устойчивости замкнутой системы, если известны амплитудно-фазовая характеристика разомкнутой системы. Этот критерий имеет большое практическое значение. Действительно, разомкнутая система представляет собой последовательное соединение объекта и регулятора При расчете САР характеристики объекта и структура регуляторов бывают уже известны, следовательно расчет амплитудно-фазовой характеристики разомкнутой системы и исследование ее устойчивости не представляет принципиальных затруднений. Однако не всякая устойчивая разомкнутая система сохраняет свою устойчивость и в замкнутом состоянии и, наоборот, неустойчивую разомкнутую систему (при неустойчивом объекте регулирования) можно сделать устойчивой в замкнутом состоянии за счет правильного выбора настроек регулятора. Применение критерия Найквиста позволяет заменить более сложную задачу исследования устойчивости замкнутой системы более простым иссле дованием разомкнутой системы. Формулировка критерия Найквиста: если разомкнутая система устойчива, или нейтральна, то замкнутая система будет устойчива в том случае, если амплитудно-фазовая характеристика разомкнутой системы не охватывает точку с координатами (1; jo)); замкнутая система будет неустойчива, если АФХ разомкнутой системы охватывает точку (1; jo)) если разомкнутая система неустойчива, то замкнутая система будет устойчива в том случае, если АФХ разомкнутой системы охватывает точку (1; jo столько раз, сколько корней характеристического уравнения разомкнутой системы лежит в правой полуплоскости.

39.Качество процессов автоматического регулирования. Как уже указывалось, одной из основных проблем, возникающих при построении систем автоматического регулирования, является проблема устойчивости. Однако это не единственная проблема. Сутце-отвует и другая, не менее важная - проблема качества процессов, регулирования. Действительно, создание только устойчивых систем, находящихся вблизи от границы устойчивости и не обладающих запасом устойчивости, не может удовлетворить ни одну реальную систему, так как любая флуктуация параметров может вывести систему из устойчивости режима. Таким образом, запас устойчивости САР является одним из показателей ее качества. Запас устойчивости может быть задан различно в зависимости от типа критерия устойчивости: для критерия Михайлова это будет окружность определенного .тадиусп г. центром в начале координат (рис.4.1а), для Найквиста - якружность с центром в точке ( /, ⁱ⁰ ) (рис.4.16) в плоскости корней характеристического уравнения - линии в левой полуплоскости, находящиеся на определенном расстоянии от мнимой оси и т.д. Наиболее распространенными критериями качества, применяемыми в

40.Статическая и динамическая ошибки регулирования, время регулирования. автоматике, являются: статическая ошибка регулирования уст.), кото рая равна разности между установившимся значением регулируемой величины и ее заданным значением y_зад. динамическая ошибка регулирования y_дин равная наибольшему отклонению в переходном процессе регулируемой величины от ее установившегося значения время регулирования Т , которое приближенно определяется как время, за которое разность между текущим значением регулируемой величины и ее заданным значением y_зад (или y_уст ) становится меньше Е

41.Степени устойчивости, колебательности, затухания. степень устойчивости п, которая характеризует запас устойчивости в плоскости корней характеристического уравнения и равна расстоянию до мнимой оси ближайшего корня (или пары корней) Степень устойчивости характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса. Причем, чем меньше абсолютное значение корня, тем медленнее зату хает У( (рис.4.5). Очевидно, что затухание свободного движения у_св , равного сумме у,- , определяется наиболее мецленно затухающей составляющей, т.е. наименьшим по абсолютному значению корнем характеристического уравнения. Представим себе теперь два колебательных процесса с одинаковой огибающей, но разной частотойПри одинаковой степени устойчивости качество этих процессов существенно отличается друг от друга, в частности скорость изменения координаты увеличивается с увеличением частоты. Следовательно степени устойчивости оказывается недостаточно для оценки качества колебательных переходных процессов. степенью колебательности М называется модуль отношения действительной и мнимой частей корня характеристического уравнения, имеющего минимальное по сравнению с другими корнями значение этого отношения Если в плоскости корнгй характеристического уравнения устойчивой системы провести из начала координат два луча ОА и ОБ (рис.4.7а) таким образом, чтобы одна пара комплексных сопряженных корней находилась на этих лучах, а все остальные корни лежали слева от них, то тангенс угла, заключенного между лучам* и мнимой осью будет равен отношению действительной и мнимой частей корней, лежащих на этих лучах, и является степенью колебательности данной системы, так как для любой другой пары корней это отношение больше Количественной оценкой интенсивности затухания колебательных процессов может служить степень затухания f ,равная У1-У3/У1степень колебательности, так же как и степень устойчивости, характеризует интенсивность затухания колебательной составляющей за один период. Для всего переходного процесса, который может включать несколько колебательных составляющих, степень колебательности характеризует затухание наиболее медленно затухающей составляющей.

42.Интегральные критерии качества. Одно из достоинств интегральных критериев состоит в том, что для их вычисления не требуется построение самого процесса регулирования, которое часто сопряжено с определенными трудностями. Оценка может производиться по некоторым промежуточный характеристикам, которыми ми обычно располагаем при проектировании САР. Линейиьй интегральный критерий Ул , служащий .для оценки качества неколебательных процессов и определяемый формулой Геометрически критерий Ул характеризует площадь, заключенную между кривой процесса регулирования и осью абцисс (рис.4.В). Очевидно, что увеличение динамической ошибки и времени регулирования приводит к увеличению и УлВеличину этого критерия можно вычислить без построения про цесса регулирования, если известна передаточная функция замкнутой системы W_зс (р) и входной сигнал Х(р) линейный интегральный критерий равен произведению передаточ ной функции на изображение по Лапласу входного сигнала, взятых при р= о Модульный критерийи применяется для оценки качества колебательных процессов (для неколебательных процессов он совпадает с линейным критерием). Модульный критерий применяется обычно при использовании для расчета GAP вычислительной техники, когда операция взятия модуля не представляет трудности. интегральный квадратичный критерии -У_кв - наиболее распространенный критерий качества Необходимо отметить, что в квадратичный критерий разные по величине ординаты переходного процесса входят с разным весом: наибольшее значение имеет начальный участок процесса, когда наблюдаются наибольшие отклонения регулируемой величины; "хвост" же переходного процесса практически не влияет на Укв' . Поэтому, стремясь минимизирорать Укв , мы фактически минимизируем наибольшие отклонения регулируемой величины. Квадратичный критерий, так же как и линейный, можно вычислить без построения переходного процесса, по частотной характеристике замкнутой системы и преобразованию по Фурье от входного сигнала. Для этого попользуется формула Релея, которая выводится с использование:.; преобразования Фурье от У (t) Обобщенные интегральные критерии Уоб Эта группа критериев отличается от обычного квадратичного критерия тем, что помимо ординат регулируемой величины учитывают так же и ее производные. Простейшим примером обобщенного критерия может служить критерий, учитывающий y(t) и скорость ее изменения Каким же образом используются все рассмотренные критерии ка-чества? Прежде всего необходимо отметить, что обеспечить оптимальные (наилучшие) значения одновременно всех показателей качестве невозможно. Например, повышение степени устойчивости и степени колебательности, т.е. увеличение запаса устойчивой системы, приводит к снижению скорости регулирования, а это влечет за собой увеличение .динамической погрешности регулирования. С другой стороны, при использовании какого-либо одного критерия можно получить бесчисленное множество процессов, удовлетворяющих этому критерию. На рис.4.9 приведены три процесса, имеющие одинаковые значения Укв но существенно отличающиеся друг от друга по динамическим ошиб-кам, времени регулирования и степени затухания.

43. Основные сведения о законе регулирования. В составе структуры САР содержится управляющее устройство, которое называется регулятором и выполняет основные функции управления, путем выработки управляющего воздействия U в зависимости от ошибки (отклонения), т.е. U = f(D ). Закон регулирования определяет вид этой зависимости без учёта инерционности элементов регулятора. Закон регулирования определяет основные качественные и количественные характеристики систем.Различают линейные и нелинейные законы регулирования. Кроме того, законы регулирования могут быть реализованы в непрерывном виде или в цифровом. Цифровые законы регулирования реализуются путем построения регуляторов с помощью средств вычислительной техники (микро ЭВМ или микропроцессорных систем).Рассмотрим основные линейные законы регулирования. Простейшим является пропорциональный закон и регулятор в этом случае называют П- регулятором. При этом U=U₀+kD , где U₀-постоянная величина, k - коэффициент пропорциональности. Основным достоинством П - регулятора является простота. По существу, это есть усилитель постоянного тока о коэффициентом усиления k. Недостатки П - регулятора заключаются в невысокой точности регулирования, особенно для объектов с плохими динамическими свойствами. Интегральный закон регулирования и соответствующий И - регулятор реализует следующую зависимость: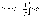 где Т -постоянная времени интегрирования. Техническая реализация И - регулятора представляет собой усилитель постоянного тока с емкостной отрицательной обратной связью. И - регуляторы обеспечивают высокую точность в установившемся режиме. Вместе с тем И - регулятор вызывает уменьшение устойчивости переходного процесса и системы в целом. Пропорционально-интегральный закон регулирования позволяет объединить положительные свойства пропорционального и интегрального законов регулирования. В этом случае ПИ - регулятор реализует зависимость: Мощным средством улучшения поведения САР в переходном режиме является введение в закон регулирования производной от ошибки. Часто эта производная вводится в пропорциональный закон регулирования. В этом случае имеем пропорционально-дифференциальный закон регулирования, регулятор является ПD- регулятором, который реализует зависимость: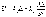 Кроме ПИ и ПД регуляторов, часто на практике используют ПИД -регуляторы, которые реализуют пропорционально–интегрально- дифференциальный закон регулирования: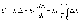 Среди нелинейных законов регулирования наиболее распространены релейные законы. Существуют двухпозиционный и трехпозиционный законы регулирования. Аналитически двухпозиционный закон регулирования записывается следующим образом: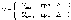 Трехпозиционный закон регулирования имеет следующий вид:

На рис 1.5. представлены в графическом виде релейные законы регулирования. При трехпозиционном законе регулирования величина D _Н определяет зону нечувствительности регулятора. Применение релейных законов позволяет при высоком быстродействии получить такие результаты, которые невозможно осуществить с помощью линейных законов,

Рис 1.5. Релейные законы регулирования

44. Пропорциональный закон регулирования Закон регулирования: Зависимость, по которой формируется регулирующее воздействие u(t) на объект из первичной информации: g(t) и/или x(t) и, возможно, f (t). Под законом регулирования (управления) понимается алгоритм или функциональная зависимость, определяющая управляющее воздействие u(t) на объект: u(t) = F(x, g, f) она же в операторной форме записи: (1*)u(t) = x(t) [k1 + k2/p + k3/p2 + ... + k4 p + k5 p2 + ...] . Наличие в (1*) чувствительности регулятора к пропорциональной, к интегральным или к дифференциальным составляющим в первичной информации x(t) определяет тип регулятора: # P пропорциональный .# I — интегральный. # PI — пропорционально интегральный (изодромный). # PD — пропорционально дифференциальный .# и более сложные варианты — PID, PIID, PIDD, Пропорциональный закон регулирования имеет вид: u(t) = Wрег(p) x(t) = k1x(t) тогда в разомкнутом состоянии система будет характеризоваться ПФ:W(p) = W_рег(p) W_o(p) = k₁W_o(p) .Рассмотрим уравнение ошибки В установившемся режиме p→0 (все производные равны нулю); W_o(p)→k_o; W(p)→k₁k_o=k; где k — контурный коэффициент усиления разомкнутой системы (при  W_ос(p)=1).Резюме: P-регулирование позволяет уменьшить установившуюся (статическую) ошибку, но только в 1+k раз, поэтому регулирование будет статическим. Т.е. при любом k x_уст≠0.

45. Интегральный закон регулирования

Интегральный закон регулирования имеет вид:u(t) = W_рег(p) x(t) = k₂/p x(t) ,тогда в разомкнутом состоянии система будет характеризоваться ПФ:W(p) = W_рег(p) W_o(p) = k₂/p W_o(p) .Рассмотрим уравнение ошибки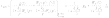 В установившемся режиме p→0, => W(p)→∞; => первая составляющая ошибки g₀/∞→0. Ошибка от возмущения зависит от вида функции W_f(0) и может быть отлична от нуля.Резюме: I-регулирование позволяет исключить статическую ошибку в системе, т.е. система будет астатической по отношению к задающему воздействию g(t).

46. Дифференциальный закон регулирования Дифференциальный закон регулирования описывается уравнением

xр (t ) = − S 2 ∆y ′(t ) где S2 – параметр настройки, которое является уравнением идеального дифференцирующего звена. На практике дифференциальный закон может быть реализован лишь приближенно в определенном интервале частот. Дифференциальная составляющая вводится в закон регулирования для того, чтобы увели чить быстродействие регулятора, так как в этом случае регулятор реагирует не на абсолютное значение регулируемой величины, а на скорость ее изменения. Дифференциальный регулятор не применяется для регулирования, так как при любом постоянном значении регулируемой величины выходной сигнал такого регулятора равен нулю

47. Пропорционально-дифференциальный закон регулирования.Пропорционально-дифференциальный закон регулирования опи-сывается уравнением

xp (t ) = −[ S1∆y (t ) + S 2 ∆y ′(t )] . ЭТОТ РЕГУЛЯТОР ПО СУЩЕСТВУ СОСТОИТ ИЗ ДВУХ ПАРАЛЛЕЛЬНО ВКЛЮЧЕННЫХ СОСТАВЛЯЮЩИХ: ПРОПОРЦИОНАЛЬНОЙ И ДИФФЕРЕНЦИРУЮЩЕЙинамические характеристики ПД-регулятора:– передаточная функция

W ( s) = −( S1 + С точки зрения качества процесса регулирования в замкнутой АСР пропорционально-дифферен-

циальный регулятор обладает особенностями обоих законов регулирования (рис. 5.61). Наличие воздействия по производной от ∆y(t) увеличивает быстродействие регулятора, благодаря чему уменьшается динамическая ошибка по сравнению с пропорциональным регулятором.S 2 s)

48.Пропорционально-интегральный закон регулирования. Пропорционально-интегральный закон регулирования описывается уравнение t 0 x p (t ) = − ( S1∆ y (t ) + S 0 ∫ ∆y (τ)dτ) и представляет собой параллельное соединение пропорциональной и интегральной составляющих.Динамические характеристики ПИ-регулятора: Пропорционально-интегральный регулятор сочетает в себе достоинства П- и И-законов регулирования, а именно: пропорциональная составляющая обеспечивает достаточноебыстродействие регулятора, а интегральная составляющая ликвидирует статическую ошибку регулирования. Переходный про-цесс в АСР с ПИ регулятором. В начале процесса регулирования основную роль играет пропорциональная составляющая, так как интегральная составляющая зависит не только от абсолютного значения, но и от времени. С увеличением времени возрастает роль интегральной составляющей, обеспечивающей устранение статической ошибки

49.Пропорционально-интегрально-дифференциальный закон регулирования. Пропорционально-интегрально-дифференциальный закон регулирования описывается уравнением xp (t ) = −( S1∆y (t ) + S 0 ∫ ∆y (τ)dτ + S 2 ∆y ′(t )) . (интеграл от t-0) ПИД-регулятор сочетает в себе достоинства всех трех простейших законов регулирования: высокое

быстродействие благодаря наличию импульса по производной от ∆y(t) и отсутствие статической

ошибки, которое обеспечивает интегральная составляющая

50. Переходные процессы объекта с различными регуляторами.

Необходимо отметить, что применение регуляторов с дифференциальными составляющими, несмотря на их достоинства, не всегда целесообразно, а иногда и недопустимо. Так, для объектов с

большим запаздыванием по каналу регулирования бесполезно вводить воздействие по производной от регулируемой величины, так как этот импульс будет поступать в регулятор по истечении времени чистого запаздывания после прихода возмущения, за которое в объекте могут накопиться большие отклонения. Более того, в таких случаях ПД- или ПИД-регулятор может "раскачать" объект и система потеряет устойчивость