6.1. Понятие производных высших порядков

Рассмотрим дифференцируемую функцию  . Найдем её производную  . Рассматривая   как новую функцию, продифференцируем её:

Полученную новую производную называют второй производной от функции  . Вторую производную обозначают так:

 или  .

Аналогично находится производная третьего, четвертого, и т.д. n-го порядка. Третья производная обозначается так:

Четвертая:

.

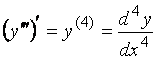Производной n – го порядка от функции   называется производная от производной  -го порядка:

.

Производные высших порядков вычисляются последовательным дифференцированием данной функции.

30 Дифференциал функции. Приближенные вычисления

Линейную функцию   называют дифференциалом функции f в точке   и обозначают df. Для функции x производная в каждой точке   равна 1, то есть   Поэтому пишут: 

Дифференциал в точке находится по формуле:   – тоже можете переписать к себе в тетрадь.

Из формулы следует, что нужно взять первую производную:

И найти её значение в точке  =64:

Таким образом:

Всё готово! Согласно формуле  :

Найденное приближенное значение достаточно близко к значению  , вычисленному с помощью микрокалькулятора.

Примечание: Когда с подбором   всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае  ), возьмите ближайшую  целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае  ). В результате и будет выполнен нужный подбор:  .

31 Теорема Ферма, Роля, Лагранжа

Теорема Ферма: если функция диффиринцируемая в точке экстремума, то производная в этой точке равна нулю

Теорема Роля: если функция непрерывна, принадлежит классу С на заданном отрезке (a;b) и на концах отрезка принимает равные значения, то существует точка x внутри интервала (a;b), производная которой равна нулю

Теорема Лагранжа: Если есть функция непрерывная класса С на заданном интервале (a;b), но на концах интервала разные значения, то есть точка S внутри этого интервала, производная которой равна приращению функции на концах интервала

32 Теорема Коши, Лопиталя

Теорема Коши: Пусть даны 2 функции непрерывные на интервале (a;b) причем g(b)-g(a) не равно нулю, тогда существует такая точка c, для которой выполняется следующее равенство:

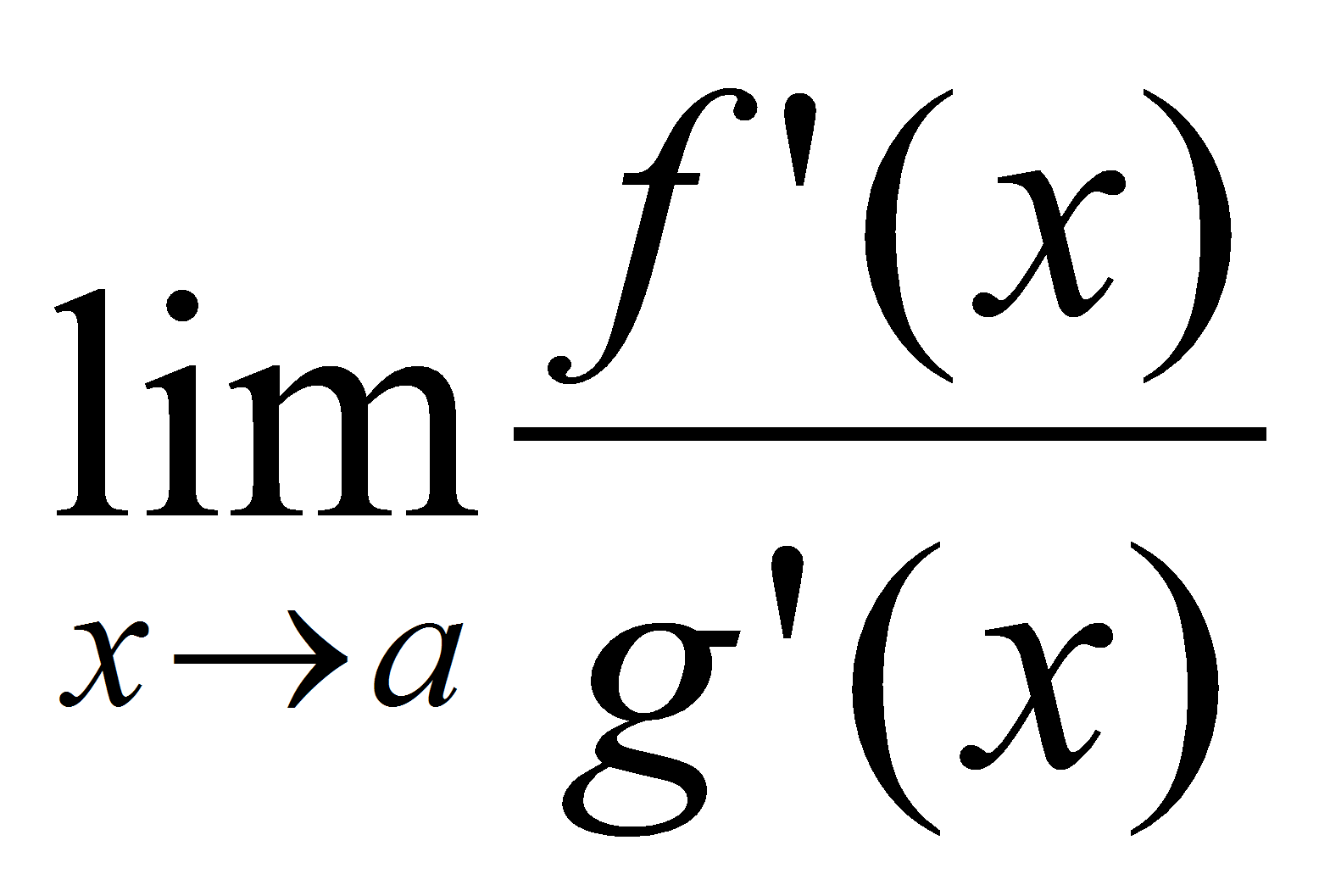Теорема Лопиталя: Пусть функции   и   дифференцируемые в некоторой окрестности точки  ,  , функции   и   либо бесконечно большие, либо бесконечно малые при   и существует предел  . Тогда существует предел .

33 Необходимые и достаточные условия для возрастания (убывания) функции. Точки экстремума

– если производная   на интервале, то функция   возрастает на данном интервале;

– если производная   на интервале, то функция   убывает на данном интервале.

Функция y=f(x) убывает на интервале X, если для любых   и  выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.