21 Бесконечно малые и бесконечно большие функции

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если   или  , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

 Функция   называется бесконечно большой при  , если  _, т.е. бесконечно большая функция – это функция, предел которой в данной точке бесконечности

22 Основные теоремы о пределах

Теорема 1. Предел константы равен самой этой константе:

 c = с.

Теорема 2. Постоянный множитель можно выносить за знак предела:

 (kа_n) = k •    а_n.

Теорема 3. Предел суммы двух переменных величин равен сумме пределов этих величин:

 (а_n + b_n) =   а_n +   b_n.

Теорема 4. Предел   произведения двух переменных величин равен произведению пределов этих величин:

 (а_n • b_n) =   а_n •   b_n.

Теорема 5. Предел дроби равен частному от деления предела числителя на предел знаменателя, если только предел знаменателя отличен от нуля:

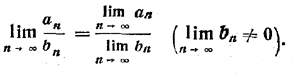
Свойства пределов 1)Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

2)Предел произведения

Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

3)Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

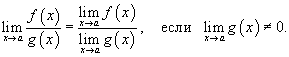
4)Теорема "о двух милиционерах"

Предположим, что   для всех x близких к a, за исключением, быть может, самой точкиx = a. Тогда, если

то

То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу L. 

23 5 основных пределов (написать от руки)

24 Сравнение бесконечно малых величин

Пусть   б.м. функции  при  . Предположим, что существует предел их отношения и он равен l.

.

Тогда если:

1)   l=1, то функции   и   называются эквивалентными б.м.;

2)   l - число, l0, то функции   и   называются б.м. одинакового порядка;

3)  l=0, то функция   называется б.м. более высокого порядка, чем  ;

4)  l= , то функция   называется б.м. более высокого порядка, чем  .

Если данный предел:   не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.

Пример 1.  ,   ,

,

 и   - эквивалентные б.м. функции.

Пример 2.   =х³,

=х,

,

,

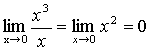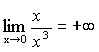 - б.м. функция более высокого порядка, чем  .

25 Непрерывные функции, точки разрыва

 Точка   называется точкой разрыва функции  , если определена на некотором интервале, для которого   служит внутренней точкой, но в самой точке  , возможно, не определена и выполняется хотя бы одно из следующих условий:

1) не существует предела слева  ;

2) не существует предела справа  ;

3) пределы слева   и справа   существуют, но не равны друг другу:  ;

4) пределы слева   и справа   существуют и равны друг другу:  , но не совпадают со значением функции в точке  :  , или функция   не определена в точке  .

Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала.