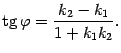3° Три вектора компланарны тогда и только тогда, когда

4°    Тройка векторов является правой тогда и только тогда, когда  . Если же  , то векторы  ,   и  образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

Если векторы  ,   и   заданы своими координатами, то их смешанное произведение вычисляется по формуле

Смешанное произведение векторов в координатах

Способ расчёта смешанного произведения векторов чисто алгебраический:

Смешанное произведение векторов  , заданных в ортонормированном базисе   правой ориентации, выражается формулой:

12 Прямая на плоскости

Например, если прямая имеет уравнение   , то расстояние от точки   до этой прямой получается из формулы (11.7) отбрасыванием третьей координаты   :

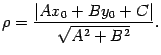
Кроме перечисленных выше формул для прямой на плоскости стоит отметить еще одну, связанную с тем, что на плоскости чаще всего используется уравнение прямой с угловым коэффициентом   , хорошо известное по школьному курсу математики.

        Предложение 11.2   Пусть заданы две прямые   и   , (  ). Тогда, если   , то угол   между этими прямыми можно найти из формулы

Если   , то прямые перпендикулярны.

13 Окружность. Эллипс

 Окружностью называется геометрическое место точек пространства, равноудаленных от одной и той же точки.

Уравнение окружности имеет вид

(x - a)² + (y - b)² = r²,

где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид

x² + y² = r².

Эллипс. Эллипсом называется геометрическое место точек пространства, для которых сумма расстояний до двух фиксированных точек (фокусов) есть величина постоянная. Простейшее уравнение эллипса:

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a² - b² = c².

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.

14 Гипербола, парабола

Гиперболой называется геометрическое место точек пространства, разность которых до двух фиксированных точек плоскости (фокусами) есть величина постоянная (2а)

Простейшее уравнение гиперболы

Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.

Параболой называется геометрическое место точек пространства, расстояние которых до фиксированной прямой, лежащей в этой плоскости (директрисой) равно расстоянию этой точки до фиксированной точки плоскости (фокуса)

Простейшее уравнение параболы

y² = 2px.     (*)

Координаты фокуса F параболы (*)  . (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)

Эксцентриситет параболы e = 1.

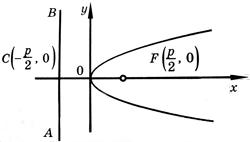y² = 2px (p > 0)

15 Плоскость

 Способы задания плоскости  Уравнением поверхности в пространстве   называется такое уравнение между переменными   которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Пусть точки   и   лежат на плоскости (рис. 11). Тогда   и, значит, их скалярное произведение равно нулю:   – это уравнение плоскости, проходящей через точку   перпендикулярно вектору  .

Укажем теперь основные уравнения плоскостей:

1)  – уравнение плоскости, проходящей через точку   перпендикулярно вектору  ;

2)   – общее уравнение плоскости (  – координаты нормали плоскости);

3)   – уравнение плоскости, проходящей через три заданные точки  ,   и  ;

4)   – уравнение плоскости в отрезках, где   -величины направленных отрезков, отсекаемых плоскостью на координатных осях   и   соответственно.

     Общее уравнение плоскости (рис. 4.13) 

  Частные случаи общего уравнения плоскости:

     1) By + Cz + D = 0 - параллельна оси Ox;

     2) Ax + Cz + D = 0 - параллельна оси Oy;

     3) Ax + By + D = 0 - параллельна оси Oz;

     4) Cz + D = 0 - параллельна оси Oxy;

     5) By + D = 0 - параллельна оси Oxz;

     6) Ax + D = 0 - параллельна оси Oyz;

     7) Ax + By + Cz = 0 - проходит через начало координат;

     8) By + Cz = 0 - проходит через ось Ox;

     9) Ax + Cz = 0 - проходит через ось Oy;

     10) Ax + By = 0 - проходит через ось Oz;

     11) z = 0 - плоскость Oxy;

     12) y = 0 - плоскость Oxz;

     13) x = 0 - плоскость Oyz.

     Приведение общего уравнения плоскости к нормальному виду:

Здесь 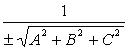  - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если   произвольно, если D = 0.

Нормальное уравнение плоскости 

где   - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.

  Расстояние от точки до плоскости 

 Угол между плоскостями 

 

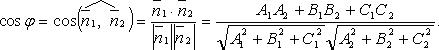
Формула комплонарности плоскостей:

 параллельны (но не совпадают)