
- •Правило сложения векторов по правилу треугольников
- •Умножение вектора на число
- •Какие векторы являются равными?
- •Базис системы векторов
- •Определение линейной зависимости системы векторов
- •Определение линейной независимости системы векторов
- •9 Скалярное произведение векторов и его свойства
- •10 Векторное произведение векторов и обозначается символом :
- •3° Три вектора компланарны тогда и только тогда, когда
- •Смешанное произведение векторов в координатах
- •12 Прямая на плоскости
- •16 Прямая в пространстве
- •16 Прямая и плоскость в пространстве
- •18 Сфера, эллипсоид, цилиндр. Конус 2 порядка
- •21 Бесконечно малые и бесконечно большие функции
- •22 Основные теоремы о пределах
- •25 Непрерывные функции, точки разрыва
- •Понятие непрерывности функции
- •26 Производная, геометрический смысл. Уравнение касательной и нормали кривой.
- •Геометрический смысл производной
- •27 Таблица производных
- •Производная функции, заданной параметрически
- •6.1. Понятие производных высших порядков
- •30 Дифференциал функции. Приближенные вычисления
- •31 Теорема Ферма, Роля, Лагранжа
- •32 Теорема Коши, Лопиталя
- •33 Необходимые и достаточные условия для возрастания (убывания) функции. Точки экстремума
- •Достаточные условия возрастания и убывания функции.
- •34 Вогнутость Функции. Асимтоты. Общая схема построения графиков функции.
- •Виды асимптот графиков Вертикальная
- •Горизонтальная
- •Наклонная
- •Связь между наклонной и горизонтальной асимптотами
Математика
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.
1. Сложение матриц - поэлементная операция
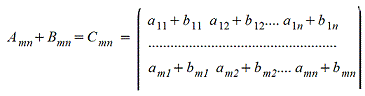
2. Вычитание матриц - поэлементная операция
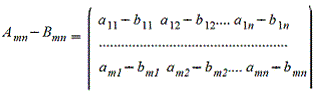
3. Произведение матрицы на число - поэлементная операция
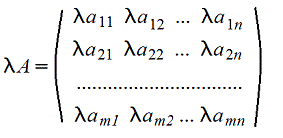
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
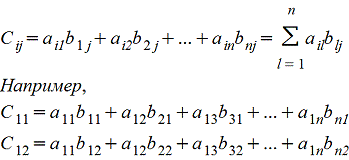
Покажем операцию умножения матриц на примере
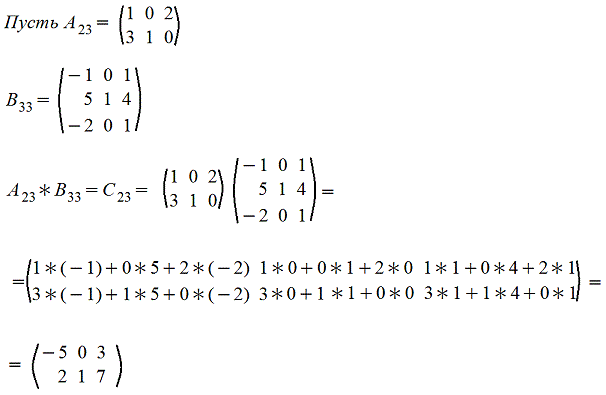
5. Возведение в степень
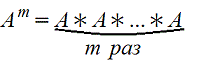
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Транспонирование – замена столбцов строками
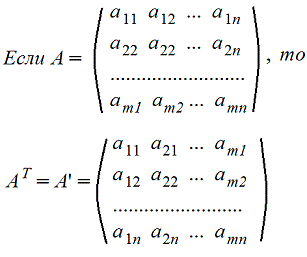
Строки и столбцы поменялись местами
2 Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.
Пример 11
Решить
систему с матричным методом
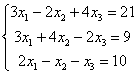
Решение:
Запишем систему в матричной форме:
![]() ,
где
,
где 
Решение
системы найдем по формуле![]() (её
подробный вывод можно посмотреть в
статье Матричные
уравнения).
(её
подробный вывод можно посмотреть в
статье Матричные
уравнения).
Согласно
формуле нам нужно найти обратную
матрицу ![]() и
выполнить матричное умножение
и
выполнить матричное умножение ![]() .
Алгоритм нахождения обратной матрицы
подробно разобран на уроке Как
найти обратную матрицу?
.
Алгоритм нахождения обратной матрицы
подробно разобран на уроке Как
найти обратную матрицу?
Обратную
матрицу найдем по формуле:
![]() ,
где
,
где ![]() –
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы ![]() .
.
Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.
Теперь
нужно вычислить 9 миноров и записать их
в матрицу миноров 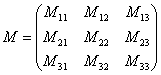
Справка: Полезно
знать смысл двойных подстрочных индексов
в линейной алгебре. Первая цифра – это
номер строки, в которой находится данный
элемент. Вторая цифра – это номер
столбца, в котором находится данный
элемент:
 То
есть, двойной подстрочный индекс
указывает, что элемент
То
есть, двойной подстрочный индекс
указывает, что элемент ![]() находится
в первой строке, третьем столбце, а,
например, элемент
находится
в первой строке, третьем столбце, а,
например, элемент ![]() находится
в 3 строке, 2 столбце
находится
в 3 строке, 2 столбце
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом:
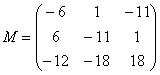 –
матрица
миноров соответствующих элементов
матрицы
.
–
матрица
миноров соответствующих элементов
матрицы
.
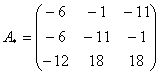 –
матрица
алгебраических дополнений.
–
матрица
алгебраических дополнений.
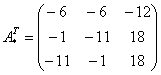 –
транспонированная
матрица алгебраических дополнений.
–
транспонированная
матрица алгебраических дополнений.
Теперь
записываем обратную матрицу:


Ответ: ![]()
Переходим
к рассмотрению правила Крамера для
системы трех уравнений с тремя
неизвестными:
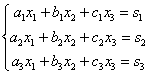
Находим
главный определитель системы:
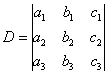
Если ![]() ,
то система имеет бесконечно много
решений или несовместна (не имеет
решений). В этом случае правило Крамера
не поможет, нужно использовать метод
Гаусса.
,
то система имеет бесконечно много
решений или несовместна (не имеет
решений). В этом случае правило Крамера
не поможет, нужно использовать метод
Гаусса.
Если ![]() ,
то система имеет единственное решение
и для нахождения корней мы должны
вычислить еще три определителя:
,
то система имеет единственное решение
и для нахождения корней мы должны
вычислить еще три определителя:
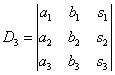
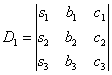 ,
,  ,
, 
И, наконец,
ответ рассчитывается по формулам:
![]()
.Пример Решить систему по формулам Крамера.
Решение:
Решим систему по формулам Крамера.
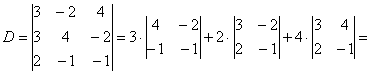
![]() ,
значит, система имеет единственное
решение.
,
значит, система имеет единственное
решение.

![]()

![]()

![]()
Ответ: ![]()
3 Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. 4 Теорема Кронекера-Капелли: Для того, чтобы система была совместна необходимо и достаточно, чтобы ранг основной матрицы был равен рангу ее расширенной матрицы
(Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов)
5 Терема Гаусса: Система линейно-алгебраических уравнений, полученная из данной систему путем линейных операций эквиваленты исходной системе
Теорема Гаусса является математическим обоснованием метода гаусса решения линейно-алгебраических систем уравнений
Линейные операции над системами линейно-алгебраических уравнений:
В данной системе можно переставлять любые 2 уравнения в этой системе в этой системе (менять местами)
Можно умножать уравнения на любое одно и тоже число не равное нулю
К одному уравнению системы можно добавить второе уравнение системы, умноженное на какое-либо число
Вектором называется направленныйотрезок, для которого указано его начало и конец:
Правило сложения векторов по правилу треугольников
Рассмотрим
два произвольных ненулевых вектора ![]() и
и ![]() :
:
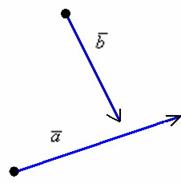
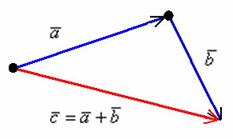
Требуется
найти сумму данных векторов. В силу
того, что все векторы считаются свободными,
отложим вектор
от конца вектора
:
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность
векторов записывают привычным значком
параллельности: ![]() ,
при этом возможна детализация:
,
при этом возможна детализация: ![]() (векторы
сонаправлены) или
(векторы
сонаправлены) или ![]() (векторы
направлены противоположно).
(векторы
направлены противоположно).
Произведением ненулевого
вектора
на
число ![]() является
такой вектор
,
длина которого равна
является
такой вектор
,
длина которого равна ![]() ,
причём векторы
и
сонаправлены
при
,
причём векторы
и
сонаправлены
при ![]() и
противоположно направлены при
и
противоположно направлены при ![]() .
.
Правило
умножения вектора на число легче понять
с помощью рисунка:
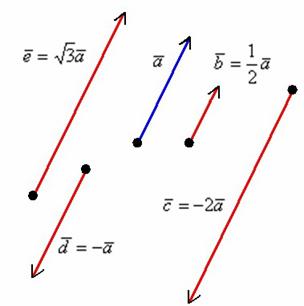
Разбираемся более детально:
1) Направление. Если множитель отрицательный, то вектор меняет направление на противоположное.
2) Длина.
Если множитель заключен в пределах ![]() или
или ![]() ,
то длина вектора уменьшается.
Так, длина вектора
,
то длина вектора уменьшается.
Так, длина вектора ![]() в
два раза меньше длины вектора
в
два раза меньше длины вектора ![]() .
Если множитель
по
модулю больше единицы, то длина
вектора увеличивается в
раз.
.
Если множитель
по
модулю больше единицы, то длина
вектора увеличивается в
раз.
3) Обратите
внимание, что все
векторы коллинеарны,
при этом один вектор выражен через
другой, например, ![]() . Обратное
тоже справедливо:
если один вектор можно выразить через
другой, то такие векторы обязательно
коллинеарны. Таким образом: если
мы умножаем вектор на число, то получится
коллинеарный (по
отношению к исходному)вектор.
. Обратное
тоже справедливо:
если один вектор можно выразить через
другой, то такие векторы обязательно
коллинеарны. Таким образом: если
мы умножаем вектор на число, то получится
коллинеарный (по
отношению к исходному)вектор.
4)
Векторы ![]() сонаправлены.
Векторы
сонаправлены.
Векторы ![]() и
и ![]() также
сонаправлены. Любой вектор первой группы
противоположно направлен по отношению
к любому вектору второй группы.
также
сонаправлены. Любой вектор первой группы
противоположно направлен по отношению
к любому вектору второй группы.
Какие векторы являются равными?
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».
С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.
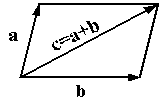 правило
параллелограмма
правило
параллелограмма
7
Базис системы векторов
Базисом системы векторов A1 , A2 ,..., An называется такая подсистема B1, B2 ,...,Br (каждый из векторов B1,B2,...,Br является одним из векторов A1 , A2 ,..., An), которая удовлетворяет следующим условиям: 1. B1,B2,...,Br линейно независимая система векторов; 2. любой вектор Aj системы A1 , A2 ,..., An линейно выражается через векторы B1,B2,...,Br
r — число векторов входящих в базис.
Определение линейной зависимости системы векторов
Система векторов A1, A2,...,An называется линейно зависимой, если существует ненулевой набор чисел λ1,λ2,...,λn, при котором линейная комбинация векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет ненулевое решение. Набор чисел λ1, λ2,...,λn является ненулевым, если хотя бы одно из чисел λ1, λ2,...,λn отлично от нуля.
