7. Расчет кривой распределения давления. Опредиление оптимального, допустимого и предельного давления на приеме насоса.Сравнение расчётных и фактических показателей.

Расчет для скважины № 2068.

Исходные данные, характеризующие режим работы скважины, приведены в таблице 7.1.

Таблица 7.1 - Исходные данные режима работы скважины

Параметры	Значение параметра
Глубина скважины	Lс=1170 м
Глубина спуска НКТ	LНКТ = 940 м;
Наружный диаметр НКТ	Дн=73 мм=0,073 м
Внутренний диаметр колонны НКТ	Дт = 59 мм= 0,059 м
Диаметр штанговой колонны	Дшт =19 мм = 0,019 м
Диаметр эксплуатационный колонны	Дэк=146 мм =0,146 м
Внутренний диаметр эксплуатационной колонный,	Дэк вн = 130 мм = 0,13 м
Плотность дегазированной нефти	нд = 892 кг/м3
Плотность пластовой воды,	в =1190 кг/м3
Плотность газа (при стандартных условиях),	ст г =1,21 кг/м3
Относительная плотность азота по воздуху	а = 0,97 кг/м3
Вязкость нефти,	н =32·10-3 Па·с
Газовый фактор,	Г0 = 13,5 м3/ м3
Давление насыщения нефти,	Рнас = 2,8МПа
Устьевое давление,	Ру = 0,62 МПа
Средняя температура скважины,	Тск = 298 К
Объёмная обводнённость,	в= 0,15
Дебит скважины по жидкости	Qж = 8,2 м3/сут
Давление на забое,	Рзаб = 3,6 МПа

Решение целого ряда технологических задач добычи нефти, а именно определение и установление рационального способа извлечения продукции на поверхность, определение оптимального режима работы скважин, а также выбор необходимого оборудования для его обеспечения связано с проведением гидродинамических расчетов движения многофазного потока продукции скважины в различных элементах ее конструкции и, в первую очередь, в колонне подъемных труб. В конечном итоге гидравлический расчет сводится к построению профиля давления в работающей скважине р = f (H), который позволяет определить давление как в любой точке колонны подъемных труб, так и на забое. Успешное решение технологических задач зависит от правильности использования расчетных зависимостей, учитывающих особенности реального газожидкостного потока.

Эквивалентный диаметр канала:

, (7.1)

где,

D_нкт – диаметр НКТ, м;

D_шт – диаметр штанг, м.

Расчет производим «сверху-вниз».

Общее число задаваемых давлений:

n=N+1, (7.2)

где,

N – число интервалов.

Принимаем величину шага изменения давления:

ΔР =0,1·Р_нас=0,1∙2,8=0,28 МПа.

По формуле определяем число интервалов:

N=(Р_нас-Р_у)/ ΔР =(2,8-0,62)/0,28=7,78≈8.

По формуле (7.2) определяем общее число задаваемых давлений:

n=8+1=9.

Рассчитаем средний геотермический градиент скважины:

ω= , (7.3)

где,

L_с - глубина скважины, м;

Т_пл – пластовая температура, К.

ω=

_{Температурный градиент потока:}

ω_n= , (7.4)

где,

ω – средний геотермический градиент скважины, К/м;

ω_n=

Определяем температуру на устье скважины:

Т_у=Т_пл– ω_nН , (7.5)

где,

Т_пл – пластовая температура, К;

ω_n – температурный градиент потока, К/м;

Н – глубина скважины, м.

Т_у=298-0,0197∙1170=274,8 К.

Вычисляем температуру потока соответствующую заданным давлениям:

Р₁=0,62 МПа.

Т₁=274,8 К.

Т₂=Т_у-[(Т_пл-Т_у)(Р-Р_у)]/(Р_заб-Р_у) , (7.7)

где,

Т_у – температура на устье скважины, К;

Т_пл – пластовая температура, К;

Р – заданное давление, МПа;

Р_у – давление на устье скважины, МПа;

Р_заб – забойное давление, МПа.

Т₂= 274,8-[(298-274,2)(0,9-0,62)]/(3,6-0,62)=277 К.

Рассчитаем текущее равновесное давление насыщения:

, (7.8)

где,

Г – газовый фактор, м³/м³;

у_с1 – мольное содержание метана, д.ед.;

у_а – мольное содержание азота, д.ед.;

Т – заданная температура, К.

Находим приведенный к нормальным условиям удельный объем выделившегося газа, предварительно определив вспомогательные коэффициенты.

, (7.9)

Р_нас – давление насыщения, МПа.

m(T)=1+0,029(T-293)(ρ_нд∙ρ_го∙10^-3-0,7966) , (7.10)

ρ_нд – плотность дегазированной нефти, кг/м³;

ρ_го – плотность газа, кг/м³.

m(Т)=1+0,029(274,8-293)(892·1,21∙10^-3-0,7966)=0,851

Д(Т)=10^-3∙ρ_нд∙ρ_го[4,5-0,00305(T-293)]-4,785 (7.11)

Д(Т)=10^-3∙892∙1,21[4,5-0,00305(274,8-293)]-4,785=0,132

Находим приведенный к нормальным условиям удельный объем выделенного газа:

V_гв(P,T)=Г∙R(P)∙m(T)∙[(Д(T)∙(1+R(P))-1] , (7.12)

V_гв(Р,Т)=13,5∙(-0,451)∙0,851∙[0,132∙(1+(-0,451))-1]=4,808 м³/м³

Рассчитываем остаточную газонасыщенность нефти (удельный объем растворенного газа) в процессе ее разгазирования:

V_гр(P,T)=Г∙m(T) - V_гв(P,T) (7.13)

V_гр(Р,Т)=13,5∙0,851-4,808=6,682 м³/м³

Определяем относительную плотность выделившегося газа

ρ_гв(Р,Т)=a[ρ_го-0,0036(1+R(P))(105,7+U∙R(P)] , (7.14)

где,

a=1+0,0054·(T-293) (7.15)

a=1+0,0054·(274,8-293)=0,902

U=10^-3∙ρ_нд∙Г-186 (7.16)

U=10^-3∙892∙13,5-186=-173,958

ρ_гв (Р,Т)=0,902·[1,21-0,0036·(1-0,451)·(105,7-173,958∙(-0,451)]=0,763

Находим относительную плотность растворенного газа, остающегося в нефти при данных условиях ее разгазирования:

_(7.17)

ρ_гр(Р,Т) =13,5·[0,902∙0,851∙1,21– 0,763∙[ 4,808/13,5]]/ 6,682=1,328

Рассчитаем объемный коэффициент, предварительно определив удельное приращение объема нефти за счет единичного изменения ее газонасыщенности (λ) и температурного коэффициента объемного расширения дегазированной нефти α_n:

_(7.18)

Так как 860≤ ρ_нд≤960 , то:

α_n= (7.19)

α_n= 1/град

Объемный коэффициент найдем по следующей формуле:

(7.20)

Вычисляем коэффициент сжимаемости газа, предварительно определив приведенные параметры газа:

, (7.21)

где,

ρ_гу – относительная по воздуху плотность смеси газов;

ρ_гу=(ρ_г – ρ_а·у_а)/(1–у_а) , (7.22)

где,

ρ_г – относительная плотность газа;

ρ_а – относительная плотность азота по воздуху;

у_а – молярная доля азота при стандартных условиях.

ρ_гу=(0,763-0,97·0,17)/(1-0,17)=0,72

(7.23)

Так как и , то

_(7.24)

_где,

_{Zy – коэффициент сверхсжимаемости углеводородной части газа:}

Определим коэффициент сверхсжимаемости азота z_a:

(7.25)

Коэффициент сверхсжимаемости газовой смеси, состоящей из углеводородных компонентов и азота, определится по следующей формуле:

z=z_y·(1-y_а)+z_a·y_a (7.26)

z=0,971·(1-0,17)+1·0,17=0,976

Вычисляем удельный объем газожидкостной смеси при соответствующих термодинамических условиях. Например, для термодинамических условий устья Т_у=274,1 К и Р_у=1,1 МПа:

(7.27)

где,

β_в – обводненность продукции, д.ед.;

R_г – удельный расход газа в случае газлифтной эксплуатации скважин.

Так как в нашем случае скважина эксплуатируется ШГН, то R_г=0, и формула примет следующий вид:

(7.28)

V_cм=1,007+4,808·0,1·274,8/(0,62·273)+0,15/(1-0,15)=1,945

Определим удельную массу смеси при стандартных условиях

М_см=_нд+Г·_го+ _в·β_в/(1- β_в) (7.29)

М_см=892+1,21·13,5+1190·0,15/(1-0,15)=1111,63 кг/м³

Рассчитаем идеальную плотность газожидкостной смеси:

(7.30)

Определяем корреляционный коэффициент необратимых потерь

давления:

(7.31)

где,

Q_ж – дебит жидкости, м³/сут;

Вычисляем полный градиент давления в точках с заданными давлениями, меньшими чем Р_нас. Например, градиент в точке при Р=Р_у.

(7.32)

Рассчитаем приведенную скорость жидкости в сечении колонны, где Р>Р_нас:

(7.33)

F – площадь сечения колонны, м².

Вычисляем число Рейнольдса и определяем режим движения ГЖС:

(7.34)

_{Так как полученное число Рейнольдса меньше критического значения, равного 2300, то можно сделать вывод о том, что режим движения ГЖС в данной зоне является ламинарным.}

_{Определяем коэффициент гидравлического трения потока:}

(7.35)

Рассчитаем градиенты давления где, р≥р_нас:

(7.36)

Вычисляем величины dP/dH, обратные расчетным dH/dP :

dH/dP=1/0,00807=123,92 м/МПа

Численно интегрируем зависимость dH/dP=f(P), последовательно определяя положение сечений с заданными термодинамическими условиями газожидкостного потока:

Р=0,9 МПа H=(123,92+112,54)/2=118,2 м;

Р=1,18 МПа Н=(123,92+105,74)/2+112,54=227,4 м и т.д.

Определим длину участка однофазного потока:

Полная расчетная длина колонны НКТ, на интервале которой давление изменяется от Р_у=0,62 МПа до Р_заб=3,6 МПа составит:

Н_р=820,12+129,52=946,64 м.

Результаты дальнейших расчетов основных параметров по методу Баксендела представлены в таблице 7.2.

Таблица 7.2 - Результаты расчетов режима движения ГЖС по методу Баксендела

Р, МПа	Т, К	Vгв, м3/м3	bн, м3/м3	z	Vcм, м3/м3	Мсм, кг/м3	ρсм, кг/м3	f	dP/dH х10-3, МПа/м	dH/dP, м/МПа	H, м
0,62	274,8	4,808	1,007	0,976	1,945	1111,63	571,41	21,03	8,070	123,92	0
0,9	277,0	3,650	1,012	0,966	1,586	1111,63	701,05	21,03	8,886	112,54	118,2
1,18	279,2	2,817	1,015	0,957	1,425	1111,63	779,98	21,03	9,457	105,74	227,4
1,46	281,4	2,158	1,018	0,948	1,339	1111,63	830,20	21,03	9,840	101,62	331,0
1,74	283,5	1,605	1,021	0,940	1,287	1111,63	863,58	21,03	10,102	98,99	431,4
2,02	285,7	1,122	1,023	0,933	1,254	1111,63	886,62	21,03	10,286	97,22	529,5
2,3	287,9	0,687	1,025	0,926	1,231	1111,63	903,03	21,03	10,418	95,99	626,1
2,58	290,1	0,287	1,028	0,919	1,215	1111,63	915,02	21,03	10,515	95,10	721,6
2,86	292,2	0	1,029	0,913	1,206	1111,63	921,84	0,080	6,211	161,00	820,1
3,6	298,0	0	1,033	0,899	1,209	1111,63	919,22	0,080	6,243	162,79	949,6

Аналогично проводим расчеты движения ГЖС в стволе скважины по методу Поэтмана-Карпентера. За диаметр канала, по которому происходит движение ГЖС, принимаем внутренний диаметр эксплуатационной колонны, равный 130 мм. Расчет производится по формулам 7.1-7.36, методом «снизу-вверх».

Результаты расчетов приведены в таблице 7.3.

Глубина спуска насоса L_н и, следовательно, давление на его приеме р_пн должны быть достаточными для обеспечения высоких коэффициентов наполнения насоса.

Необходимое давление на приеме ЭЦН зависит в первую очередь от содержания свободного газа в потоке откачиваемой газожидкостной смеси.

Результаты расчетов режима движения ГЖС по методу Поэтмана-Карпентера представлены в таблице 7.3.

По результатам расчетов строим кривую распределения давления.

Таблица 7.3 – Результаты расчетов режима движения ГЖС по методу Поэтмана-Карпентера

Р, МПа	Т, К	Vгв, м3/м3	bн, м3/м3	z	Vcм, м3/м3	Мсм, кг/м3	ρсм, кг/м3	f	dP/dH х10-3, МПа/м	dH/dP, м/МПа	H, м
3,6	298,0	0	1,033	0,992	1,209	1111,6	919,22	0,098	12,23	81,77	1170
3,32	295,8	0	1,032	0,976	1,208	1111,6	920,24	0,098	12,26	81,57	1112,3
3,04	293,6	0	1,030	0,963	1,207	1111,6	921,25	0,098	12,31	81,23	1044,2
2,76	291,3	0,053	1,029	0,954	1,207	1111,6	920,85	10223,3	14,604	68,47	984,5
2,48	289,1	0,437	1,027	0,949	1,221	1111,6	910,59	10223,3	14,593	68,53	912,2
2,2	286,9	0,849	1,024	0,946	1,239	1111,6	897,05	10223,3	14,581	68,58	823,8
1,92	284,7	1,298	1,022	0,946	1,265	1111,6	878,59	10223,3	14,570	68,64	742,4
1,64	282,4	1,802	1,020	0,949	1,304	1111,6	852,54	10223,3	14,564	68,66	665,2
1,36	280,2	2,385	1,017	0,954	1,365	1111,6	814,38	10223,3	14,582	68,58	581,3
1,08	274,3	2,957	1,011	0,960	1,452	1111,6	765,68	10223,3	14,654	68,24	515,4

На рисунке 7.1 представлена кривая распределения давления НКТ и в стволе скважины.

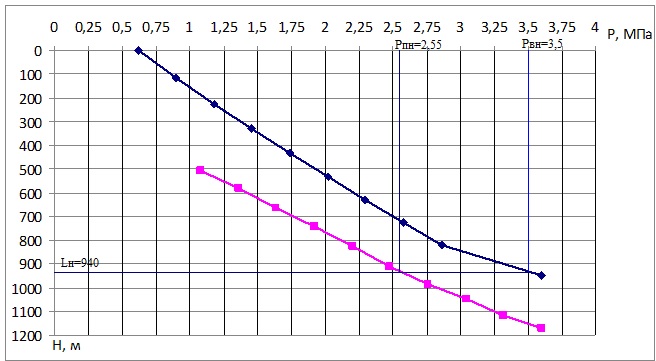
Рисунок 7.1. – Кривая распределения давления в НКТ и в стволе скважины

По кривой распределения давления выбираем давление на приеме и на выходе насоса, используя глубину спуска насоса, которую принимаем на основании промысловых данных:

L_н=940 м; Р_пн=2,55 МПа; Р_вн=3,5 МПа.

Таким образом, в результате расчета кривой распределения давления, определили давление на приеме насоса, которое равно 2,5 МПа и на выкиде насоса 3,5 МПа.

Рассчитаем оптимальное, допустимое и предельное давление на примере скважины №1223 на Акташской площади. Имеем следующие начальные значения:

1) Объемная обводнённость, В=0,15 д.ед.;

2) Вязкость нефти, _нп = 32 ·10^-3 Па·с;

3) Вязкость дегазированной нефти, _нд= 106·10^-3 Па·с;

4) Давление насыщения, Р_нас= 2,8 Мпа

Оценка оптимально давления на приеме выполняется по следующим формулам:

Р_опт = µ_нд/µ_нп·Р_нас·(6,97·В-4,5·В²-2,43) (7.37)

где

В – объемная обводнённость продукции, д.ед.;

Р_нас – давление насыщения, Мпа.

Р_опт= (106·10^-3/32·10^-3) ·2,8·10⁶·(6,97·0,15-4,5·0,15²-2,43) = 2,5 Мпа

Для оценки допустимого давления на приеме насоса выполняется по следующим формулам:

Р_доп = µ_нд/µ_нп·Р_нас· (2,62·В-1,75·В²-0,85) (7.38)

Р_доп=(106·10^-3/32·10^-3) ·2,8·10⁶·(2,62·0,15-1,75·0,15²-0,85) = 1,9Мпа

Предельное давление на приеме во всей области объемной обводненности 0≤ В ≤1 можно рассчитать по зависимости:

Р_доп = µ_нд/µ_нп·Р_нас· (0,125-0,115·В) (7.39)

Р_доп= (106·10^-3/32·10^-3) ·2,8·10⁶·(0,125-0,115·0,15) = 0,9 Мпа

Вопрос выбора соответствующего давления на приеме УЭЦН представляет сложную технико-экономическую задачу и является одним из принципиальных, определяя эффективность работы всей системы