4.Статический анализ причин выхода из строя скважин и технологических параметров работы осложненного фонда скважин
Для условий Акташской площади Ново-Елховского месторождения основными факторами, осложняющими эксплуатацию скважин УЭЦН являются отложения солей, наличие в продукции скважин механических примесей, кривизна ствола скважины, высокая вязкость продукции, образование стойких водонефтяных эмульсий, а в ряде случаев коррозионная активность среды.
Наиболее серьёзные осложнения и отказы оборудования возникают в связи с отложениями парафина, солей на забое скважины, в подъёмных трубах, в наземном и подземном оборудовании и т. д.
В таблице 4.1 представлены неисправности ЭЦН скважин Акташской площади Ново-Елховского месторождения, встречающиеся в процессе эксплуатации. В основном это обрыв НКТ по резьбе, отложение солей на приеме насоса, водонефтяные эмульсии и прочие отложения (резина, футеровка НКТ, и т.д.).
Остальные неисправности встречаются в незначительном количестве или вовсе отсутствуют.
Таблица 4.1 - Характерные неисправности УЭЦН за период 2010-2012 годы
Причины неисправности ЭЦН |
2010 |
2011 |
2012 |
всего |
1 |
2 |
3 |
4 |
5 |
Выход из строя кабеля |
- |
1 |
- |
1 |
Обрыв НКТ по резьбе |
2 |
2 |
1 |
5 |
Коррозионное отверстие в НКТ |
1 |
- |
1 |
2 |
Отлoжeниe сoли нa пpиeмe нacоса |
1 |
2 |
1 |
4 |
Выход из строя скважин по причине АСПО |
_ |
1 |
1 |
2 |
Продолжение таблицы 4.1
1 |
2 |
3 |
4 |
5 |
Наличие водонефтяной эмульсии |
2 |
3 |
1 |
6 |
Всего |
6 |
9 |
5 |
20 |
На рисунке приведены причины выхода из строя скважин с УЭЦН на Акташской площади Ново-Елховского месторождения за 2010-2012 года.
Рисунок 4.1 - Причины выхода из строя скважин с УЭЦН на Акташской площади за 2010-2012 года
Из таблицы 4.1 и рисунка 4.1 видно, что самым значительным техническим фактором, влияющим на работу установок ЭЦН и являющимися причинами выхода из строя скважин на Акташской площади можно назвать обрыв НКТ по резьбе, водонефтяные эмульсии а так же отложение солей (сульфата и карбоната кальция) на приеме насоса. Отсюда следует, что осложнения являются важным фактором влияющим на срок службы ЭЦН, а борьба с ними должна привести к увеличению межремонтного периода установки.
При статистической обработке экспериментальных материалов в первую очередь необходимо установить, существует ли связь между двумя или несколькими факторами, и какова степень влияния каждого из рассматриваемых факторов и их сочетаний на исследуемый процесс.
Осложненный фонд скважин с УЭЦН на Акташской площади Ново-Елховского месторождения за три года составляет 20 скважин.
Таблица 4.2 – Технологические параметры работы осложненного фонда
№ скважины |
Qн, т/сут |
Qж, т/сут |
B, % |
Глубина спуска насоса, м |
1 |
4 |
15 |
82,1 |
1150 |
2 |
3 |
9 |
85,6 |
1600 |
3 |
9 |
8 |
62 |
737,8 |
4 |
7 |
19 |
75 |
722,1 |
5 |
5 |
21 |
68 |
995 |
6 |
11 |
24 |
80,4 |
825,7 |
7 |
13 |
5 |
68,7 |
799,6 |
8 |
6 |
8 |
77 |
800 |
9 |
4 |
7 |
78,5 |
1550 |
10 |
3 |
11 |
87 |
1300 |
11 |
8 |
14 |
73 |
859 |
12 |
7 |
20 |
58 |
893 |
13 |
3 |
18 |
67 |
1008 |
14 |
5 |
35 |
55 |
1229 |
15 |
8 |
38 |
49 |
1144 |
16 |
6 |
16 |
54 |
1321 |
17 |
3 |
19 |
69 |
892 |
18 |
4 |
33 |
83 |
800 |
19 |
7 |
28 |
72 |
918 |
20 |
5 |
34 |
49 |
1188 |
Проведем статистическую обработку по дебиту нефти. Составим таблицу интервалов с указанием граничных и средних значений дебита нефти.
Из статистической совокупности выбираем наибольшее и наименьшее значения: Xmax= 13 т/сут; Xmin = 3 т/сут. Размах: Xmax - Xmin = 13 - 3 = 10 т/сут;
Размах делим на к
равных частей:
,
где к – число интервалов
Таблица 4.3 – Статистический анализ по дебиту нефти
№ интервала |
Интервал |
Среднее значение xi* |
Частота |
Частость |
Накопленная частота |
xi-( xi +1) |
Mi |
Pi |
|||
1 |
3 - 5 |
4 |
10 |
0,5 |
10 |
2 |
5– 7 |
6 |
5 |
0,25 |
15 |
3 |
7 – 9 |
8 |
3 |
0,15 |
18 |
4 |
9 – 11 |
10 |
1 |
0,05 |
19 |
5 |
11 – 13 |
12 |
1 |
0,05 |
20 |
На рисунке 4.2 представлена зависимость интервала дебита нефти от частоты.
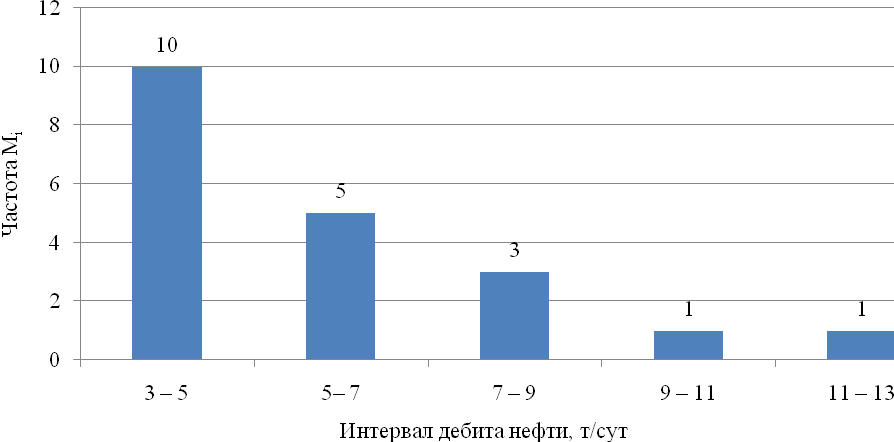
Рисунок 4.2 – Зависимость интервала дебита нефти от частоты Мi
Из рисунка 4.2 делаем вывод, что наибольшая частота приходится на дебит равный 3-5 т/сут,и равна 10 делениям единиц, при дебите от 5-7 т/сут соответственно 5 делениям единиц, при дебите 7-9т/сут частота равна 3 делениям единиц.При дебитах 9-11т/сут и 11-13т/сут частота не меняется и остается равной 1.
Рисунок 4.3 – Зависимость дебита нефти от накопленной частоты
Из рисунка 4.3 видно, что при увеличении дебита накопленная частота возрастает.
Подведем итог и рассчитаем средневзвешенное значение, среднеквадратичное отклонение, дисперсию, предельную ошибку, все эти расчеты приведены в таблице 4.4.
Таблица 4.4 – Значение дебитов нефти на Акташской площади
Средневзвешенное X |
Cреднеквадратичное отклонение σ |
Дисперсия D |
Eβ |
Ni |
5,8 |
2,03 |
4,16 |
0,89 |
17,87 |
И так из таблицы 4.4 получили средневзвешенное, которое составило 5,8, среднеквадратичное отклонение 2,03, дисперсию 4,16 и предельную ошибку 0,89.
Проведем статистическую обработку по дебиту жидкости. Составим таблицу интервалов с указанием граничных и средних значений дебитов жидкости.
Из статистической
совокупности выбираем наибольшее и
наименьшее значения: Xmax=
38 т/сут; Xmin
= 5 т/сут.
Размах: Xmax
- Xmin
= 38 - 5 = 33
т/сут;
Таблица 4.5 – Статистический анализ по дебиту жидкости
№ интервала |
Интервал |
Среднее значение xi* |
Частота |
Частость |
Накопленная частота |
xi-( xi +1) |
Mi |
Pi |
|||
1 |
5 - 11,6 |
8,3 |
5 |
0,25 |
5 |
2 |
11,6– 18,6 |
15,1 |
4 |
0,2 |
9 |
3 |
18,6 – 24,8 |
21,7 |
5 |
0,25 |
14 |
4 |
24,8 – 31,4 |
28,1 |
1 |
0,05 |
15 |
5 |
31,4 – 38 |
34,7 |
4 |
0,2 |
19 |
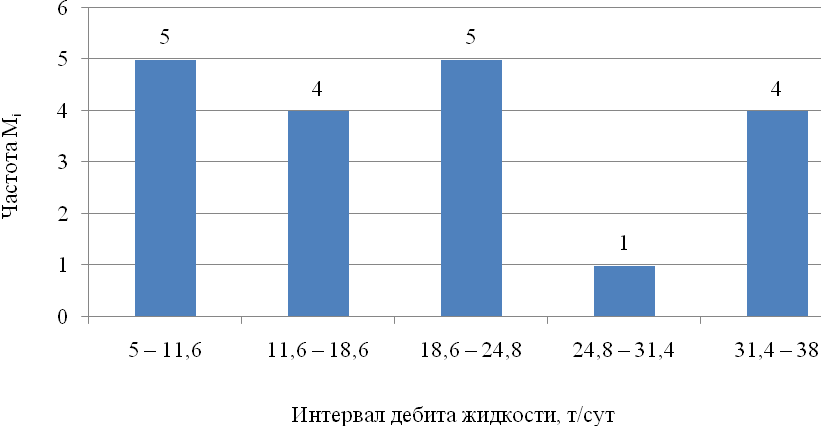
Рисунок 4.4 – Зависимость интервала дебита жидкости от частоты Мi
Из рисунка 4.4 видно, что наибольшая частота достигается при дебитах 5-11,6т/сут и 18,6-24,8 т/сут, которая составляет 5 делений единиц, при дебитах 11,6-18,6 и 31,4-38 т/сут число делений составило 4 единицы, при дебите 24,8-31,4 т/сут число делений составило 1 единица.
Рисунок 4.5 – Зависимость дебита жидкости от накопленной частоты
Из рисунка 4.5 видно, что в интервале накопленной частоты от 5 до 14 и в интервале от 15 до 19 дебит жидкости возрастает более интенсивно чем в интервале от 14 до 15.
Подведем итог и рассчитаем средневзвешенное значение, среднеквадратичное отклонение, дисперсию, предельную ошибку, все эти расчеты приведены в таблице 4.6.
Таблица 4.6 – Значения дебитов жидкости на осложненном фонде
Средневзвешенное X |
Cреднеквадратичное отклонение σ |
Дисперсия D |
Eβ |
Ni |
18,86 |
9,28 |
86,16 |
4,06 |
81,36 |
И так из таблицы 4.6 получили средневзвешенное, которое составило 18,86, среднеквадратичное отклонение 9,28, дисперсию 86,16 и предельную ошибку 4,06.
Проведем статистическую обработку по обводненности. Составим таблицу интервалов с указанием граничных и средних значений обводненности.
Из статистической совокупности выбираем наибольшее и наименьшее значения: Xmax= 87%; Xmin = 49%. Размах: Xmax - Xmin = 87 - 49 = 38%;
Размах делим на к равных частей: ,
Таблица 4.7 – Статистический анализ по обводненности
№ интервала |
Интервал |
Среднее значение xi* |
Частота |
Частость |
Накопленная частота |
xi-( xi +1) |
Mi |
Pi |
|||
1 |
49 - 56,6 |
56,6 |
4 |
0,2 |
4 |
2 |
56,6 – 64,2 |
64,2 |
2 |
0,1 |
6 |
3 |
64,2 – 71,8 |
71,8 |
4 |
0,2 |
10 |
4 |
71,8 – 79,4 |
79,4 |
5 |
0,25 |
15 |
5 |
79,4 – 87 |
87 |
2 |
0,1 |
27 |
На рисунке 4.6 представим зависимость интервала обводненности от частоты Мi
Рисунок 4.6 – Зависимость интервала обводненности от частоты Мi
Из рисунка 4.6 видно, что наибольшая частота приходится на интервал равный 71,8-79,4 %, которая составляет 5 делений единиц, при интервалах 49-56,6 и 64,2-71,8 % число долей составило 4 единиц,при интервалах 56,6-64,2 и 79,4-87 % число долей равно 2 единицам.
Рисунок 4.7 – Зависимость обводненности от накопленной частоты
Как видно из рисунка 4.7 при увеличении обводненности накопленная частота возрастает.
Таблица 4.8 – Значения обводненности на Акташской площади
Средневзвешенное X |
Cреднеквадратичное отклонение σ |
Дисперсия D |
Eβ |
Ni |
57,2 |
13,25 |
175,63 |
5,80 |
116,16 |
И так из таблицы 4.8 получили средневзвешенное, которое составило 57,2, среднеквадратичное отклонение 13,25, дисперсию 175,63 и предельную ошибку 5,80.
Проведем статистическую обработку по глубине спуска насоса.
Из статистической совокупности выбираем наибольшее и наименьшее значения: Xmax= 1600 м; Xmin = 722,1 м. Размах: Xmax-Xmin = 1600–722,1 = 877,9 м;
Размах делим на к равных частей:
Таблица 4.9 – Статистический анализ по глубине спуска насоса
№ интервала |
Интервал xi-( xi +1) |
Среднее значение xi* |
Частота Mi |
Частость Pi |
Накопленная частота |
1 |
722,1 – 879,68 |
800,89 |
6 |
0,3 |
6 |
2 |
879,68 –1073,2 |
976,44 |
4 |
0,2 |
10 |
3 |
1073,2 – 1248,8 |
1161 |
4 |
0,2 |
14 |
4 |
1248,8 – 1424,4 |
1336,6 |
3 |
0,15 |
17 |
5 |
1424,4 – 1600 |
1512,2 |
3 |
0,15 |
20 |
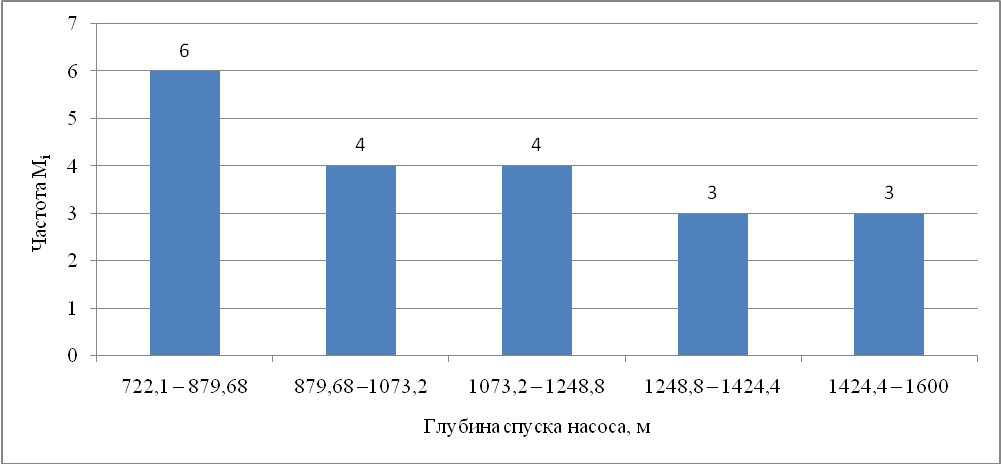
Рисунок 4.8 - Зависимость глубины спуска насоса от частоты Mi
Из рисунка 4.8 видно, что наибольшая частота приходится на глубину равную 7221-879,68 м, в которой число скважин составило 6 единиц.
Рисунок 4.9 – Зависимость глубины спуска насоса
от накопленной частоты
Подведем итог и рассчитаем средневзвешенное значение, среднеквадратичное отклонение, дисперсию, предельную ошибку, все эти расчеты приведены в таблице 4.10.
Таблица 4.10 – Расчеты глубины спуска насоса
Средневзвешенное X |
Cреднеквадратичное отклонение σ |
Дисперсия D |
Eβ |
Ni |
1021 |
91,57 |
838,6 |
40,13 |
802 |
И так из таблицы 4.10 получили средневзвешенное, которое составило 1021, среднеквадратичное отклонение 91,97, дисперсию 838,6 и предельную ошибку 40,13.
Можно сделать вывод, что применение статистической обработки промысловых данных по технологическим параметрам работы осложненного фонда дает возможность установить более точные значения показателей технологических параметров работы скважин и режима эксплуатации.
В таблице 4.11 приведена распределение скважин по типу насоса.
Таблица 4.11- Распределение скважин по типу насоса
Тип насоса |
Количество скважин |
Доля от действующего фонда скважин с УЭЦН, % |
ЭЦНМ5 |
20 |
45 |
ЭЦНА5 |
16 |
36 |
ЭЦН5 |
5 |
11 |
ЭЦН |
3 |
8 |
Итого |
44 |
100 |
Рисунок 4.10- Распределение скважин по типу насоса на Акташской площади Ново-Елховского месторождения
Делая вывод по главе, можно отметить, что осложненный фонд скважин с УЭЦН за 2010-2012 года составил 20 единиц. Наиболее распространенными причинами выхода из строя скважин с УЭЦН на Акташской площади Ново-Елховского месторождения за три года является обрыв НКТ по резьбе, водонефтяные эмульсии а так же отложение солей (сульфата и карбоната кальция) на приеме насоса. Также нужно сказать, проведение статистического анализа промысловых данных по технологическим параметрам работы осложненного фонда дает возможность установить более точные значения показателей технологических параметров работы скважин и режима эксплуатации.