1. Эконометрика, её задачи и методы

Эконометрика – это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.

Задача эконометрики состоит в выявлении связей между количественными характеристиками экономических объектов в целях построения математических правил прогноза (вычисления приближённых значений) недоступных для наблюдения количественных характеристик объектов по наблюденным или заданным значениям других количественных характеристик объектов.

Эмпирическим материалом для построения правил прогноза (эти правила именуются эконометрическими моделями) служат результаты наблюдений за изучаемыми экономическими объектами. Или, другими словами, ставится задача придать количественные оценки выводам и закономерностям, сформулированным в общей экономической теории.

Принципы эконометрики:

• Правильная постановка проблемы.

• Системная направленность.

• Попытка учета рыночной неопределенности.

• Улучшение имеющихся и поиск новых альтернатив.

Методы: статистический и математический

К статистическим и математическим методам относят сводку и группировку информации, корреляционный и информационный анализ, вариационный и регрессионный анализ, статистические уравнения зависимости.Сводка и группировка информации по определенным признакам проводится при наличии 25 единиц.При группировке совокупность делят на группы, выделяют основные типы и формы явлений.Рассматривают изменение признака от одной группы к другой, изучают зависимость результата признака от факторов, положенных в основание группы.При построении интервалов необходимо учитывать степень заполнения интервалов единицами совокупности, применение не равных интервалов, если изучаются неоднородные совокупности.

Дисперсионный анализ – логическое продолжение группировок.Для оценки вариации, обусловленной тем или иным признаком, совокупность разделяется на группы по признаку, влияния которого исследуется.Согласно правилу сложения дисперсии для расчета используется общую внутри группы и остаток дисперсий.

Математическими методами изучается зависимости.

• 
Классические методы математики.

• 
Регрессионный – корреляционный анализ.

• 
Исследование операций в теории массового обслуживания.

2 Этапы построения эконометрических моделей

Процесс (комплекс решаемых задач) построения экономических моделей можно условно разбить на несколько этапов. Отметим, что это деление условное и различные авторы такое деление производят по-разному. Это относится к количеству этапов, но не к комплексу задач, которые необходимо решить в процессе построения модели.

Мы будем рассматривать четыре основных этапа:

• спецификация модели;

• сбор исходной информации; идентификация модели;

• анализ адекватности модели.

Спецификация модели. На этом этапе исследователю необходимо подробно изучить качественные закономерности поведения экономического объекта, выявить количественные показатели, характеризующие объект, сформулировать взаимосвязи между этими показателями.

Результатом такой работы должна быть формализованная (выраженная на математическом языке) запись поведения объекта.

Спецификация модели - подробное описание на математическом языке закономерностей поведения экономического объекта.

Второй этап построения модели – это сбор исходной информации. Имея запись спецификации модели, понятно, за какими переменными модели необходимо пронаблюдать и зафиксировать значения. В результате выполнения этого этапа в распоряжении исследователя появляются необходимые для построения модели данные, которые принято называть выборкой.

Третий этап построения модели: этап оценивания (идентификации) модели. Его называют математическим, вычислительным или идентификационным. Любая случайная величина характеризуется присущим ей законом распределения (функцией плотности вероятности для непрерывных случайных величин). Законы распределения случайных величин содержат параметры. По определению оценка – это приближенное значение параметра.

3. Типы данных, используемых в эконометрических исследованиях: пространственные данные, временные ряды, панельные данные

В эконометрических моделях в основном используются данные трёх типов:

1) пространственные данные

2) временные ряды

3) панельные данные

Пространственными данными называется совокупность экономической информации, которая характеризует различные объекты, однако полученной за один и тот же период или момент времени.

Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности.Примером пространственных данных может служить комплекс экономической информации по какому-либо предприятию (численность работников, объём производства, размер основных фондов), объёмах потребления продукции определённого вида, данные о ВВП различных стран в каком-либо конкретном году и т. д.

Временными данными называется совокупность экономической информации, которая характеризует один и тот же объект, но за разные периоды времени.

Отдельно взятый временной ряд можно рассматривать как выборку из бесконечного ряда значений показателей во времени.Примером временных данных могут служить данные о динамике индекса потребительских цен, ежедневные обменные курсы валют.

Отличия временных данных от пространственных данных:

1) единицы временных рядов подвержены явлению автокорреляции (зависимости между прошлыми и текущими наблюдениями временного ряда), т. е. они не являются статистически независимыми в отличие от единиц случайной пространственной выборки;

2) единицы временных рядов не являются одинаково распределёнными величинами;

3) в отличие от пространственных данных временные данные естественным образом упорядочены во времени.

Панельными данными называются данные, содержащие сведения об одном и том же множестве объектов за ряд последовательных периодов времени.

Панельные данные являются обобщением или комбинацией пространственных и временных данных.Примером панельных данных могут служить показатели хозяйственной деятельности совокупности предприятий, которые собираются каждый год.В этом случае мы получим массив данных, в котором содержатся и данные об однородных объектах за один и тот же период времени, и последовательные значения одной экономической переменной в различные периоды времени.Но если совокупность предприятий из года в год будет различна, то такие данные уже не будут панельными.

4. Типы переменных в эконометрических моделях Коэффициент корреляции и индекс детерминации

В эконометрических моделях результативный признак называется объясняемой переменной, а факторный признак называется объясняющей переменной.

В эконометрическом моделировании выделяют следующие виды экономических переменных:

1) экзогенные или независимые переменные (х), значения которых задаются извне. В определённой степени экзогенные переменные поддаются управлению;

2) эндогенные или зависимые переменные (у), значения которых определяются внутри модели;

3) лаговые переменные – это экзогенные или эндогенные переменные, которые относятся к предыдущим моментам времени и находятся в эконометрической модели одновременно с переменными, относящимися к текущему моменту времени. Например, xt-1 – это лаговая экзогенная переменная, а yt-1 – это лаговая эндогенная переменная;

4) предопределённые или объясняющие переменные – это лаговые (xt-1) и текущие (х) экзогенные переменные, а также лаговые эндогенные переменные (yt-1).

5) фиктивные переменные используются в эконометрических моделях для характеристики явления или процесса, в отношении которого нет данных по качественному признаку;

6) переменные-заместители искусственно вводятся в эконометрическую модель для характеристики явления или процесса, который не может быть количественно охарактеризован. При этом переменная-заместитель тесно коррелирует с этим явлением.

Корреляция – связь, гле воздействие отдельных факторов проявляется только как тенденция при массовом наблюдении фактических данных.

Коэф. Корреляции -   r_x,y= cov_x,y/S_x*S_y, где   cov_x,y = 1/h-1 (x_i - x_cp)(y_i - y_cp) – отклонение

Смысл – не принимают значения > 1. Знак показывает характер зависимости(оба растут/убывают = +)

Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.

Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:

Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:

Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.

Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной.Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.

5. Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции.

 Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи массовых процессов и явлений.Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного или нескольких факторов.

Для оценки тесноты и существенности связи между двумя коррелированными признаками используется линейный коэффициент корреляции.

В практике применяются различные математические формулировки этого коэффициента. Приведем три из них:

Линейный коэффициент корреляции изменяется в пределах от -1 до 1. Знаки коэффициентов регрессии и корреляции совпадают. Оценка линейного коэффициента корреляции Значение линейного коэффициента корреляции Характер связи Интерпретация связи r =0 отсутствует - 0 прямая с увеличением Х увеличивается У -1 обратная с увеличением Х уменьшается У и, наоборот r=1 функциональная каждому значению факторного признака строго соответствует одно значение результативного признака Для измерения тесноты связи используются также и другие показатели: корреляционное отношение (эмпирическое и теоретическое); множественный коэффициент корреляции; частные коэффициенты корреляции и некоторые другие.

6.Количественные характеристики взаимосвязи пары случайных переменных

Математическое ожидание (среднее значение), дисперсия и среднее квадратич.отклонение, ковариация и коэф-нт корреляции.

Матем. ожид.дискретн.

случ. перем. назыв. вел-на:M(x)=сумма(P_i*x_i),где M(x)-матем ожид. СДП х, P_i-вероятность появл. в опытах знач-я х_i,n-кол-во допустимых значений ДСВеличины. Матем. ожид-средневзвеш. значение ДСП,где в качестве веса использ значение вероятности.

Дисперсией дискретн случперемен назыв. в-на:D²(x)=сумма(x_i-M(x))²*P(x_i), где D²(x)-дисперсия случ.перем.х. Дисперсия случ. вел-ны выступает в качестве характеристики разброса возможных ее значений. Положит. корень из дисперсии назыв средним квадратич.отклонением или стандартным отклонением,или стандартной ошибкой.

^ Матем.ожидание непрерывн. случ. перемен Хс законом распределения р_х(t) назыв. в-на:М(х)=интеграл от – бесконечности до + бесконечности tp_x(t)dt, что назыв. перв начальн.моментом ф-ции p_x(t).Через рез-ты наблюдений матем.ожид-е вычисл.:M(x)=(1/n)сумма(x_i).

^ Дисперсией непрерывн.случ. перемен. Х с функцией плотности вероятности p_x(t) назыв. выраж-е: D²(x)= интеграл от – бесконечности до + бесконечности(t-M(x))²p_x(t)dt,что назыв вторым центр моментом ф-ции p_x(t).В общем случае дисперсия случ.перем.: D²(x)=М(х-М(х))²=М(х²)-М²(х).

Ковариацией двух случ.перем. ХиУ:COV(x,y)=M((x-M(x))(y-M(y))).Значение ковариации отраж.наличие связи между 2 случ.перем.Если COV(x,y)>0,связь между XиY положит.,если <0-отрицат., если=0,X и Y-независ.перемен.Область возможн.знач. ковариации-вся числовая ось. Недостатки устраняются путем деления знач ковариации на знач стандартн отклонений перемен,что назыв коэф-нтом корреляции.это безразмерн вел-на,предел от -1 до 1 включительно.Ф-ла:р(х,у)=COV(x,y)/(D(x)*D(y)).

7.Функциональные и корреляционные типы связей. Ковариация, корреляция

Существуют два вида связи: функциональная и корреляционная, которые обусловлены двумя типами закономерности: динамической и статистической. Для явлений, где проявляется динамические закономерности, характерна жесткая, механическая причинность, которая может быть выражена в виде уравнения четкой зависимости и т.д.Такая зависимость называется функциональной.При функциональной связи каждому значению одной величины соответствует одно или несколько вполне определенных значений другой величины.Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функций и между аргументом и функциями нельзя установить строгой зависимости, называется корреляционной. Классификация корреляционной связи: 1. по тесноте связи: отсутствует, слабая, умеренная, сильная. 2. По направлению: прямая и обратная. Если с увиличением аргумента Х функция у также увеличивается без всяких единичных исключений – полная прямая связь.Если с увеличением аргумента Х функция у уменьшается без всяких единичных исключений – полная обратная связь. 3. По форме выражения: прямолинейная и криволинейная

Наряду с функцией регрессии в эконометрике существенно используются числовые характеристики взаимосвязи пары случайных переменных (x, y). Эти характеристики именуются ковариацией и коэффициентом корреляции. Ковариацией называется константа , определенная по правилу Свойства математического ожидания позволяют представить и так: , где Оценкой ковариации служит величина , именуемая выборочной ковариацией. Так же размерность равна произведению значений размерности случайных переменных x и y. Часто удобно использовать безразмерную ковариацию Константа именуется еще коэффициентом корреляции. Всегда .

8.Ковариация, коэффициенты корреляции и детерминации. Частные коэффициенты корреляции

Наряду с функцией регрессии в эконометрике существенно используются числовые характеристики взаимосвязи пары случайных переменных (x, y). Эти характеристики именуются ковариацией и коэффициентом корреляции. Ковариацией называется константа , определенная по правилу Свойства математического ожидания позволяют представить и так: , где Оценкой ковариации служит величина , именуемая выборочной ковариацией. Так же размерность равна произведению значений размерности случайных переменных x и y. Часто удобно использовать безразмерную ковариацию Константа именуется еще коэффициентом корреляции. Всегда .

Коэффициент детерминации (R2)— это доля дисперсии отклонений зависимой переменной от её среднего значения, объясняемая рассматриваемой модельюсвязи. Модель связи обычно задается как явная функция от объясняющих переменных. где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии -среднее арифметическое зависимой переменной. Коэффициент детерминации является случайной переменной. Он характеризует долю результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака: 0≤ R2≤1. причем если R2= 1 то переменная yt полностью объясняется регрессором xt. В множественной регрессионной модели добавление дополнительных регрессоров увеличивает значение коэффициента детерминации, поэтому его корректируют с учетом числа независимых переменных:

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и фактором при устранении влияния другого фактора, которые включены в уравнение регрессии.

Показатели частной корреляции определяются как отношение сокращения остаточной дисперсии, имевшей место до введение его в регрессионную модель. Частные коэффициенты корреляции, рассчитанные по рекуррентной формуле могут находиться в пределах от -1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнивая их друг с другом можно ранжировать факторы по тесноте их связи с результатом.

9.Временные ряды и их структура

Временными данными называется совокупность экономической информации, которая характеризует один и тот же объект, но за разные периоды времени.

Отдельно взятый временной ряд можно рассматривать как выборку из бесконечного ряда значений показателей во времени.Примером временных данных могут служить данные о динамике индекса потребительских цен, ежедневные обменные курсы валют.

Отличия временных данных от пространственных данных:

1) единицы временных рядов подвержены явлению автокорреляции (зависимости между прошлыми и текущими наблюдениями временного ряда), т. е. они не являются статистически независимыми в отличие от единиц случайной пространственной выборки;

2) единицы временных рядов не являются одинаково распределёнными величинами;

3) в отличие от пространственных данных временные данные естественным образом упорядочены во времени.

Временные ряды состоят из двух элементов:

• периода времени, за который или по состоянию на который приводятся числовые значения;

• числовых значений того или иного показателя, называемых уровнями ряда.

Временные ряды классифицируются по следующим признакам:

по форме представления уровней:

• ряды абсолютных показателей;

• относительных показателей;

• средних величин.

по количеству показателей, для которых определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;

по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени.В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени.Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней.Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;

по расстоянию между датами и интервалами времени выделяют равноотстоящие — когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) — когда принцип равных интервалов не соблюдается;

по наличию пропущенных значений: полные и неполные временные ряды;

временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины.

в зависимости от наличия основной тенденции выделяют стационарные ряды, в которых среднее значение и дисперсия постоянны, и нестационарные, содержащие основную тенденцию развития

10.Выявление и устранение аномальных наблюдений во временных рядах. Под аномальнымуровнемпонимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве уровня ряда, оказывает существенное влияние на значения основных характеристик временного ряда, в том числе на соответствующую трендовую модель. Причинами аномальных наблюдений могут быть ошибки технического порядка, или ошибки первого рода: ошибки при агрегировании и дезагрегировании показателей, при передаче информации и другие технические причины. Ошибки первого рода подлежат выявлению и устранению. Кроме того, аномальные уровни во временных рядах могут возникать из-за воздействия факторов, имеющих объективный характер, но проявляющихся эпизодически, очень редко – ошибки второго рода; они устранению не подлежат. Для выявления аномальных уровней временных рядов используются методы, рассчитанные для статистических Совокупностей - Метод Ирвина, например, предполагает использование следующей формулы:

Где среднеквадратичное отклонение рассчитывается в свою очередь с использованием формул:

Расчетные значения и т. д. сравниваются с табличными значениями критерия Ирвина ‚и если оказываются больше табличных, то соответствующее значение уровня ряда считается аномальным. После Выявления аномальных уровней ряда обязательно определение причин их возникновения. Если точно установлено, что они вызваны ошибками первого рода, то они устраняются либо заменой аномальных уровней простой средней арифметической двух соседних уровней ряда, либо заменой аномальных уровней соответствующими значениями по кривой, аппроксимирующей данный временной ряд.

11.Адаптивные модели прогнозирования

Наиболее перспективными для прогнозирования рядов со столь сложной структурой являются адаптив­ные модели, в которых имеются компоненты, отражающие и тренд, и сезонные составляющие.

Наиболее часто исследователь имеет дело с новыми явлениями, характеризующиеся короткими статистическими рядами или со старыми явления­ми, претерпевающими коренные изменения. Поэтому при ис­пользовании информации для построения моделей, прежде всего, возникает вопрос о преемственности данных. Устаревшие данные при моде­лировании часто оказываются бесполезными и даже вредными. К тому же необходимо знать, не как развивается процесс в сред­нем, а как будет развиваться его тенденция, существующая в данный момент. Следовательно, нужно строить модели, опираясь в основном на малое количество самых свежих данных. В этом случае альтернативой статистическому обоснованию модели мо­жет быть наделение ее адаптивными свойствами.

Важную роль в деле совершенствования прогнозирования должны сыграть адаптивные методы. Цель адаптивных методов заключается в построении самокорректирующихся (самонастраи­вающихся) моделей, которые способны отражать изменяющиеся во времени условия, учитывать информационную ценность раз­личных членов временной последовательности и давать достаточ­но точные оценки будущих членов данного временного ряда. От­личие адаптивных моделей от других прогностических моделей состоит в том, что они отражают текущие свойства ряда и спо­собны непрерывно учитывать эволюцию динамических характе­ристик изучаемых процессов. Именно поэтому такие модели пред­назначаются прежде всего для краткосрочного прогнозирования.В основе адаптивных методов лежит простейшая модель экс­поненциального сглаживания. Модификации и обобщения этой модели привели к появлению целого семейства адаптивных мо­делей.

12. Линейная модель множественной регрессии

Построение модели множественной регрессии является одним из методов характеристики аналитической формы связи между зависимой (результативной) переменной и несколькими независимыми (факторными) переменными.

Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.

Общий вид линейной модели множественной регрессии:

Ŷ=β₀+β₁*х₁+β₂*х₂+…+β_m*x_m+ ε_i, где ŷ – теоретическое значение результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнении регрессии; x_i – значения факторных признаков, β_i – параметры уравнения(k регрессии), ε_i - случайные ошибки модели множественной регрессии.

При построении нормальной линейной модели множественной регрессии учитываются пять условий:

1) факторные переменные х_i– неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии а_i;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях: E(ε_i)=0 (i=1,m)

3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

D(ε_i)= E(ε_i²)=G²=const

4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): Cov(ε_i, ε_j)=E(ε_i, ε_j)=0 (i≠j)

Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G²: ε_i ~N(0, G²).

Общий вид нормальной линейной модели парной регрессии в матричной форме:

Y=X* β+ε

Где

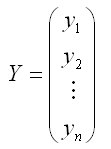–  случайный вектор-столбец значений результативной переменной размерности (n*1);

–  матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;

– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);

–  случайный вектор-столбец ошибок модели регрессии размерности (n*1).

Включение в линейную модель множественной регрессии случайного вектора-столбца ошибок модели обусловлено тем, что практически невозможно оценить связь между переменными со 100-процентной точностью.

Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:

1) факторные переменные x1j…xmj – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии εi. В терминах матричной записи Х называется детерминированной матрицей ранга (k+1), т.е. столбцы матрицы X линейно независимы между собой и ранг матрицы Х равен m+1<n;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:

где

G² – дисперсия случайной ошибки модели регрессии ε;

In – единичная матрица размерности (n*n).

4) случайная ошибка модели регрессии ε является независимой и независящей от матрицы Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G²: ε→N(0;G2In.

В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:

1) данные переменные должны быть количественно измеримыми;

2) каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;

3) факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.