2. Краткие сведения из теории моделирования системы эксплуатации пк.

1. Марковский случайный процесс – дискретный случайный процесс, в котором вероятность 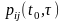зависит только от указанных в обозначении вероятности параметров: в каком состоянии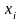 была система в момент 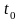и в какое другое состояние 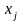система должна попасть в момент времени 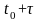. Другими словами, все вероятностные характеристики марковского случайного процесса в будущем зависят лишь от того, в каком состоянии система находится в настоящий момент времени и не зависит от того, каким образом этот процесс протекал в прошлом до момента .

Различают два типа марковских случайных процессов: с дискретным временем и с непрерывным временем.

Марковским случайным процессом с дискретным временем называется процесс, у которого переходы из одного состояния в другое возможны в строго определенные, заранее известные, неслучайные моменты времени 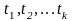. Такие процессы встречаются довольно редко.

Марковским случайным процессом с непрерывным временем называется процесс, у которого переход из одного состояния в другое (соседнее) возможен в любой момент времен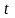и . Такие процессы тесно связаны с пуассоновскими потоками. Можно доказать, что, если процесс, протекающий в системе, является марковским с непрерывным временем, то все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими.

Если поток является пуассоновским, то справедливо следующее дифференциальное уравнени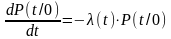е: , где - условная вероятность того, что система в момент времени t находится в некотором состоянии, вычисленная при условии, что в момент времени t=0 она находилась в том же состоянии. 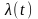- интенсивность пуассоновского потока, переводящего систему из одного состояния в другое.

Решение вышеприведенного дифференциального уравнения имеет вид .

В частном случае, когда интенсивность пуассоновского потока, переводящего систему из состояния 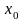в состояние 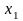, постоянная ( ), имеем .

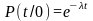Это означает, что, если на систему воздействует простейший поток событий интен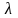сивностью , то время пребывания системы в состоянии распределено по показательному закону с параметром . Справедливо и обратное утверждение. Если время пребывания рассматриваемой системы в состоянии распределено по показательному закону с параметром , то процесс является марковским, а поток событий, под воздействием которого процесс переходит из этого состояния, простейший с интенсивностью .

В этом случае среднее время (математическое ожидание времени) пребывания системы в состоянии будет равно: .

Для сведения произвольного процесса к марковскому с непрерывным временем достаточно принять в нем все потоки событий пуассоновскими, которые определяются исчерпывающим образом своими интенсивностями. Следовательно, для сведения произвольного процесса к марковскому с непрерывным временем нужно определить интенсивности всех потоков событий, переводящие систему из состояния в состояние, и считать, что на систему воздействуют пуассоновские потоки событий с известными интенсивностями. Иногда удобнее оперировать со средним временем пребывания системы в том или ином состоянии. Это среднее время может изменяться со временем . В этом случае мгновенная интенсивность потока событий, переводящего систему из состояния , будет определяться по формуле .

Пуассоновские потоки и близкие к ним по структуре потоки событий на практике встречаются наиболее часто и описание различных систем и операций с помощью марковских случайных процессов с непрерывным временем и дискретными состояниями является достаточно точным. По крайней мере, такое описание соответствует точности исходной информации. В дальнейшем марковский случайный процесс с непрерывным временем и дискретным числом состояний будем называть марковским процессом.

Итак, марковский процесс возможен тогда, когда все потоки событий, переводящие процесс из состояния в состояние, являются пуассоновскими. Пуассоновский поток событий, переводящий систему из состояния в состояние , характеризуется одной функцией: интенсивностью потока событий , которая может быть любой неотрицательной функцией времени. Тогда исчерпывающей характеристикой марковского (случайного) процесса, имеющего состояние 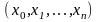, является квадратная матрица интенсивностей 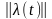порядка 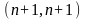, элементами которой являются интенсивности пуассоновских потоков , при этом .

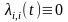
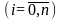Этой матрице интенсивностей соответствует ориентированный граф состояний 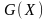, в котором размер ребра, связывающего состояние с состоянием , равен интенсивности потока событий . Если некоторая интенсивность , то на графе ребра, соединяющего состояние с состоянием , просто не будет.

Ориентированный граф состояний - граф, на котором, помимо направлений перехода, указаны также интенсивности потоков событий. То есть:

Состояние i

Состояние j

Прежде чем приступить непосредственно к аналитическому моделированию необходимо составить графовую модель процессов, происходящих в системе эксплуатации, формализующую логику взаимоотношений элементов системы.

Графовая модель отражает нахождение системы в некоторых состояниях в рассматриваемый момент времени и переходы из состояния в состояние, происходящие с определенными интенсивностями.

Если построена графовая модель, то можно определить вероятности нахождения системы в каком-либо состоянии в любой момент времени с помощью аналитической модели.