34. Ряды динамики: понятие, назначение

Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содержат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

Ряды динамики содержат два вида показателей. Показатели времени (годы, кварталы, месяцы и др.) или моменты времени (на начало года, на начало каждого месяца и т.п.). Показатели уровней ряда. Показатели уровней рядов динамики могут быть выражены абсолютными величинами (производство продукта в тоннах или рублях), относительными величинами (удельный вес городского населения в %) и средними величинами (средняя заработная плата работников отрасли по годам и т. п.). В табличной форме ряд динамики содержит два столбца или две строки.

Правильное построение рядов динамики предполагает выполнение ряда требований:

1. все показатели ряда динамики должны быть научно обоснованными, достоверными;

2. показатели ряда динамики должны быть сопоставимы по времени, т.е. должны быть исчислены за одинаковые периоды времени или на одинаковые даты;

3. показатели ряда динамики должны быть сопоставимы по территории;

4. показатели ряда динамики должны быть сопоставимы по содержанию, т.е. исчислены по единой методологии, одинаковым способом;

5. показатели ряда динамики должны быть сопоставимы по кругу учитываемых хозяйств. Все показатели ряда динамики должны быть приведены в одних и тех же единицах измерения.

Статистические показатели могут характеризовать либо результаты изучаемого процесса за период времени, либо состояние изучаемого явления на определенный момент времени, т.е. показатели могут быть интервальными ( периодическими ) и моментными. Соответственно первоначально ряды динамики могут быть либо интервальными, либо моментными. Моментные ряды динамики в свою очередь могут быть с равными и неравными промежутками времени.

Первоначальные ряды динамики могут быть преобразованы в ряд средних величин и ряд относительных величин (цепной и базисный). Такие ряды динамики называют производными рядами динамики.

Методика расчета среднего уровня в рядах динамики различна, обусловлена видом ряда динамики. На примерах рассмотрим виды рядов динамики и формулы для расчета среднего уровня.

35. Виды рядов динамики: моментные, интервальные

Интервальные ряды динамики

Уровни интервального ряда характеризуют результат изучаемого процесса за период времени: производство или реализация продукции ( за год, квартал, месяц и др. периоды), число принятых на работу, число родившихся и.т.п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени.

Средний уровень в интервальных рядах динамики ( ) исчисляется по формуле средней арифметической простой:

• y — уровни ряда (y₁, y₂ ,...,y_n),

• n — число периодов (число уровней ряда).

Рассмотрим методику расчета среднего уровня интервального ряда динамики на примере данных о продаже сахара в России.

Годы	Продано сахара, тыс. тонн
1994	2905
1995	2585
1996	2647

- это среднегодовой объем реализации сахара населению России за 1994-1996 гг. Всего за три года было продано 8137 тыс.тонн сахара.

Моментные ряды динамики

Уровни моментных рядов динамики характеризуют состояние изучаемого явления на определенные моменты времени. Каждый последующий уровень включает в себя полностью или частично предыдущий показатель. Так, например, число работников на 1 апреля 1999 г. полностью или частично включает число работников на 1 марта.

Если сложить эти показатели, то получим повторный счет тех работников, которые работали в течение всего месяца. Полученная сумма экономического содержания не имеет, это расчетный показатель.

В моментных рядах динамики с равными интервалами времени средний уровень ряда исчисляется по формулесредней хронологической:

• y -уровни моментного ряда;

• n -число моментов (уровней ряда);

• n — 1 — число периодов времени (лет, кварталов, месяцев).

Рассмотрим методику такого расчета по следующим данным о списочной численности работников предприятия за 1 квартал.

	Число работников
на 1 января	150
на 1 февраля	145
на 1 марта	162
на 1 апреля	166

Необходимо вычислить средний уровень ряда динамики, в данном примере — среднюю списочную численность работников предприятия:

Расчет выполнен по формуле средней хронологической. Средняя списочная численность работников предприятия за 1 квартал составила 155 человек. В знаменателе — 3 месяца в квартале, а в числителе (465) — это расчетное число, экономического содержания не имеет. В подавляющем числе экономических расчетов месяцы, независимо от числа календарных дней, считаются равными.

В моментных рядах динамики с неравными интервалами времени средний уровень ряда исчисляется по формуле средней арифметической взвешенной. В качестве весов средней принимается продолжительность времени ( t- дни, месяцы ). Выполним расчет по этой формуле.

Списочная численность работников предприятия за октябрь такова: на 1 октября — 200 человек, 7 октября принято 15 человек, 12 октября уволен 1 человек, 21 октября принято 10 человек и до конца месяца приема и увольнения работников не было. Эту информацию можно представить в следующем виде:

Число работников	Число дней (период времени)
200	6 (с 1 по 6 включительно)
215	5 (с 7 по 11 включительно)
214	9 (с 12 по 20 включительно)
224	11 (с 21 по 31 включительно)

При определении среднего уровня ряда надо учесть продолжительность периодов между датами, т. е. применятьформулу средней арифметической взвешенной:

В данной формуле числитель ( ) имеет экономическое содержание. В приведенном примере числитель (6665 человеко-дней) — это календарный фонд времени работников предприятия за октябрь. В знаменателе (31 день) — календарное число дней в месяце.

В тех случаях, когда имеем моментный ряд динамики с неравными интервалами времени, а конкретные даты изменения показателя неизвестны исследователю, то сначала надо вычислить среднюю величину ( ) для каждого интервала времени по формуле средней арифметической простой, а затем вычислить средний уровень для всего ряда динамики, взвесив исчисленные средние величины продолжительностью соответствующего интервала времени  . Формулы имеют следующий вид:

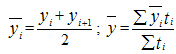
Рассмотренные выше ряды динамики состоят из абсолютных показателей, получаемых в результате статистических наблюдений. Построенные первоначально ряды динамики абсолютных показателей могут быть преобразованы в ряды производные: ряды средних величин и ряды относительных величин. Ряды относительных величин могут быть цепные (в % к предыдущему периоду) и базисные (в % к начальному периоду, принятому за базу сравнения — 100%). Расчет среднего уровня в производных рядах динамики выполняется по другим формулам.