80. Векторная диаграмма.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) — фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой^[1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.

81. Сложение нескольких гармонических колебаний одного направления.

 Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

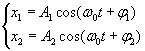 (4.1)

Уравнение результирующего колебания будет иметь вид

Убедимся в этом, сложив уравнения системы (4.1)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

 (4.2)

Можно найти такие величины А и φ0 , чтобы удовлетворялись уравнения

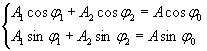(4.3)

Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

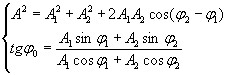
Подставляя (4.3) в (4.2), получим:

Или окончательно, используя теорему косинусов суммы, имеем:

Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

 

 

 

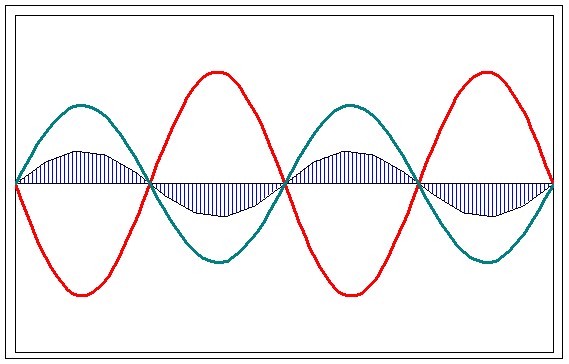
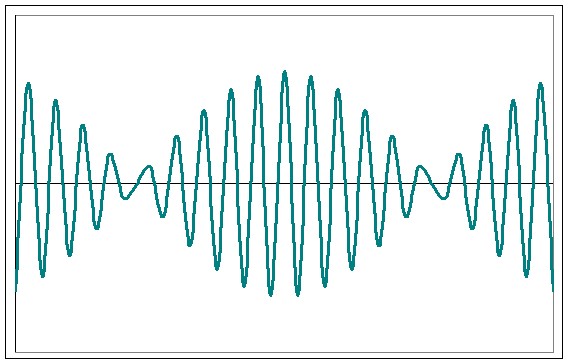
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

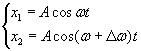
Решим систему

Решение системы:

Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:

Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω

Период биений: