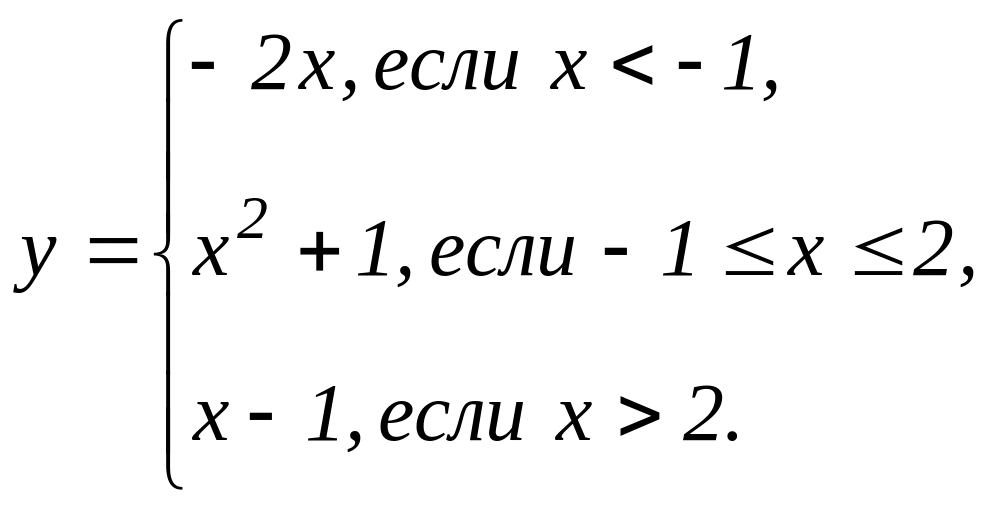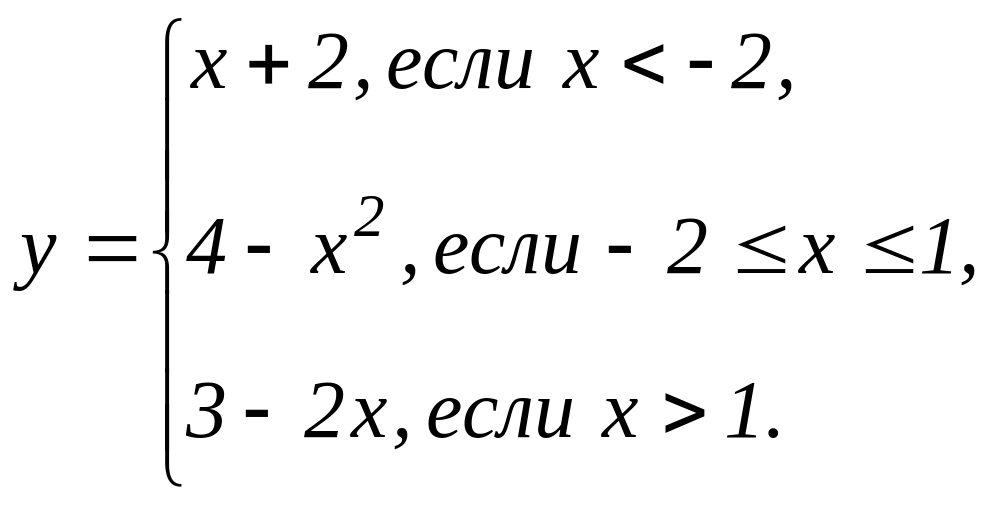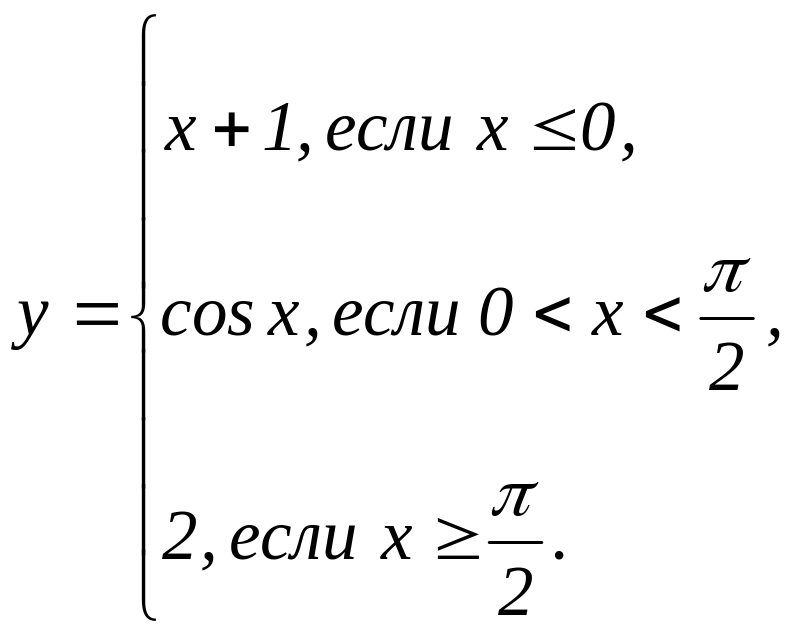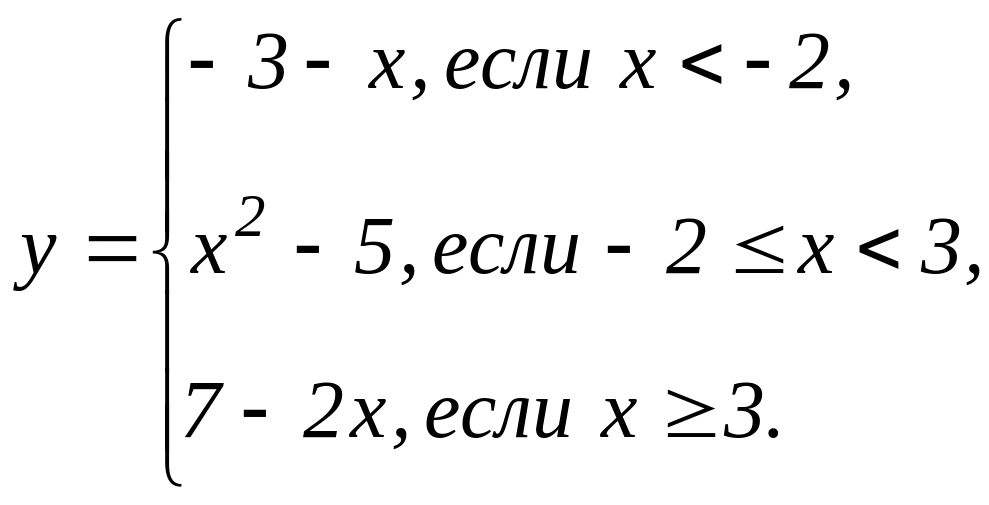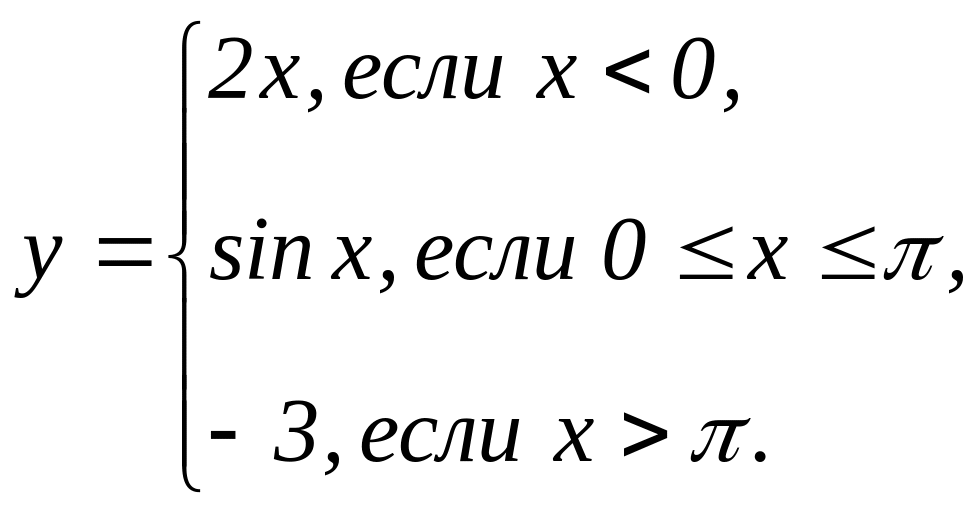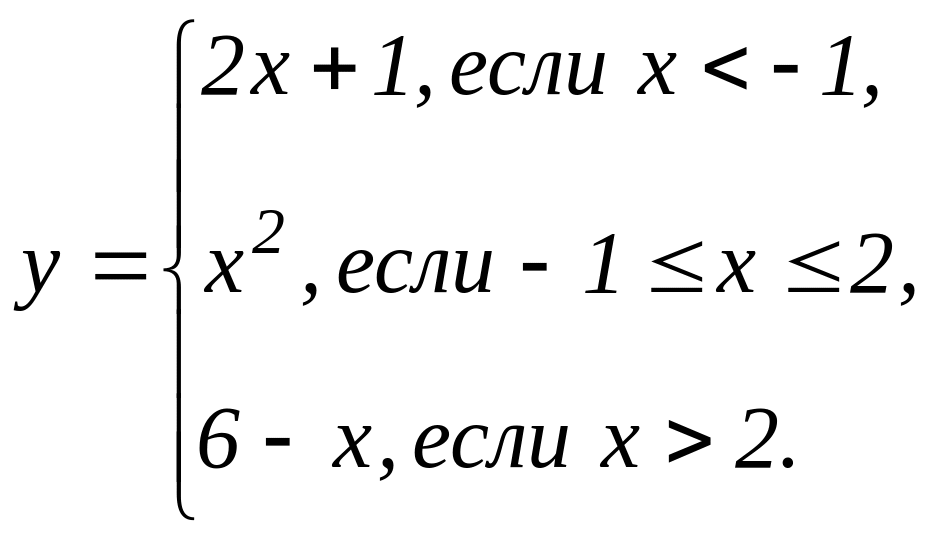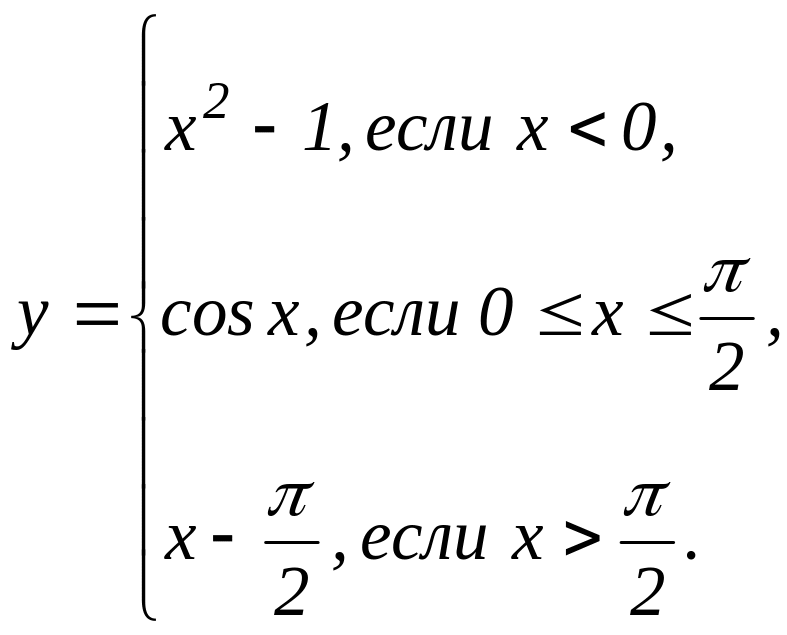Задания.

В задачах 1-10 систему уравнений записать в матричной форме и решить ее матричным способом.

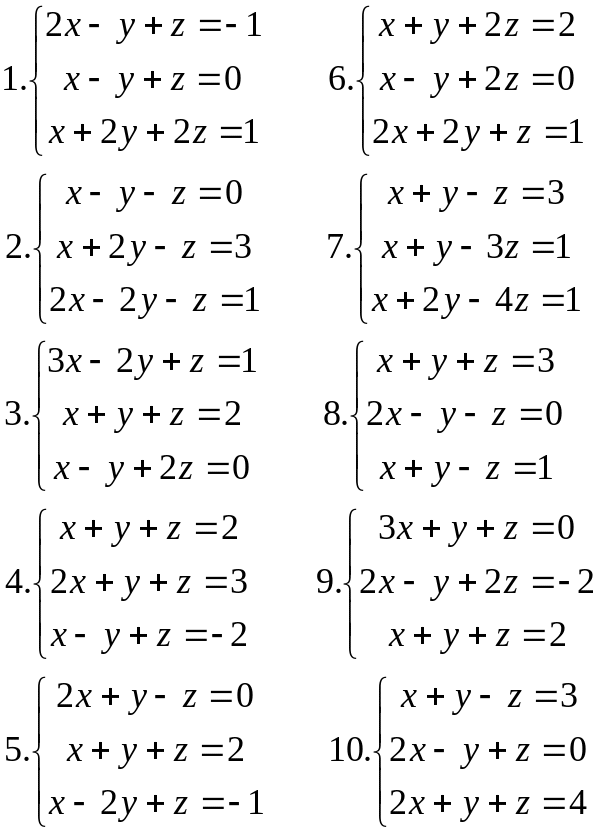
В задачах 11-20:

Предприятие производит продукцию трех видов и использует сырье двух типов. Нормы затрат сырья на единицу продукции каждого вида заданы матрицей А. Стоимость единицы сырья каждого типа задана матрицей В. Каковы общие затраты предприятия на производство k единиц

продукции 1-го вида, m единиц продукции 2-го вида и n единиц продукции 3-го вида.

В задачах 21-30 вычислить пределы:

В задачах 31 - 40 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) сделать чертеж.

31.		36
32		37
33		38
34		39
35.		40

41-50 Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

41

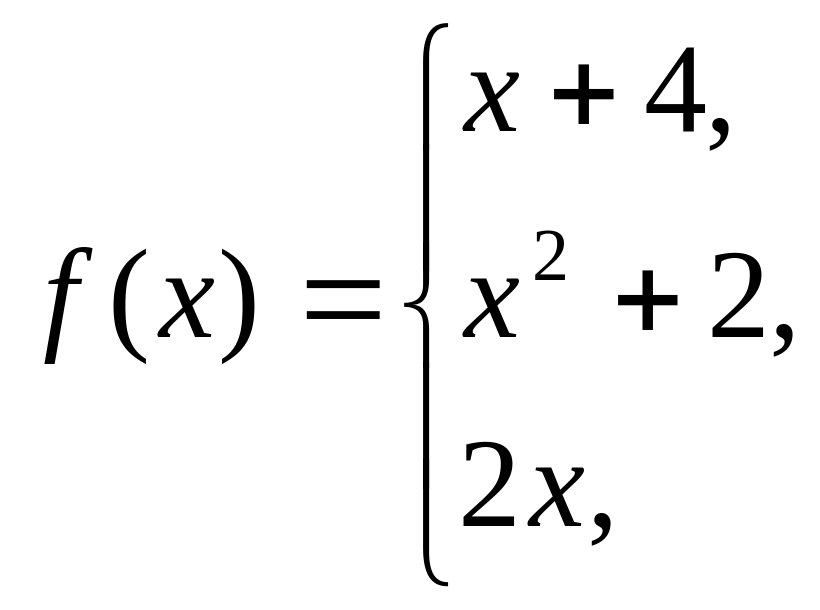
42

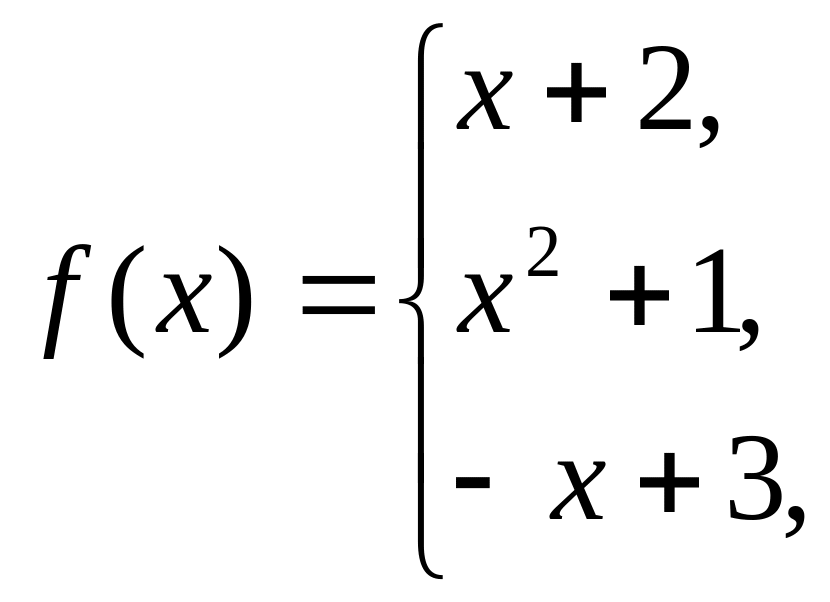
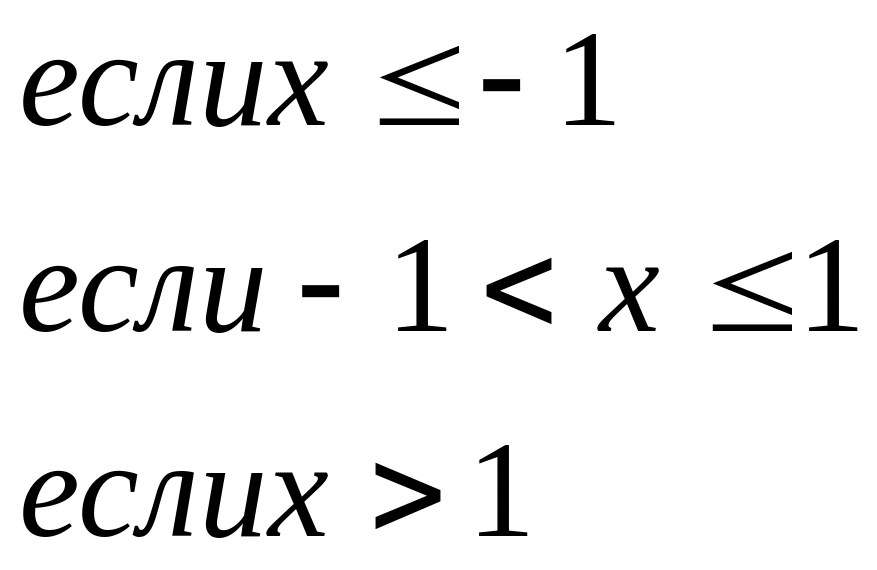
43

44

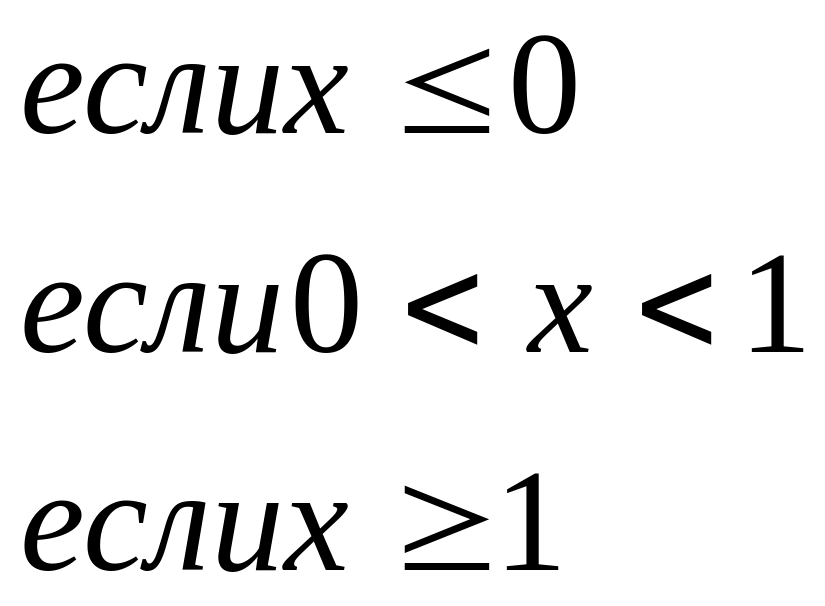
45

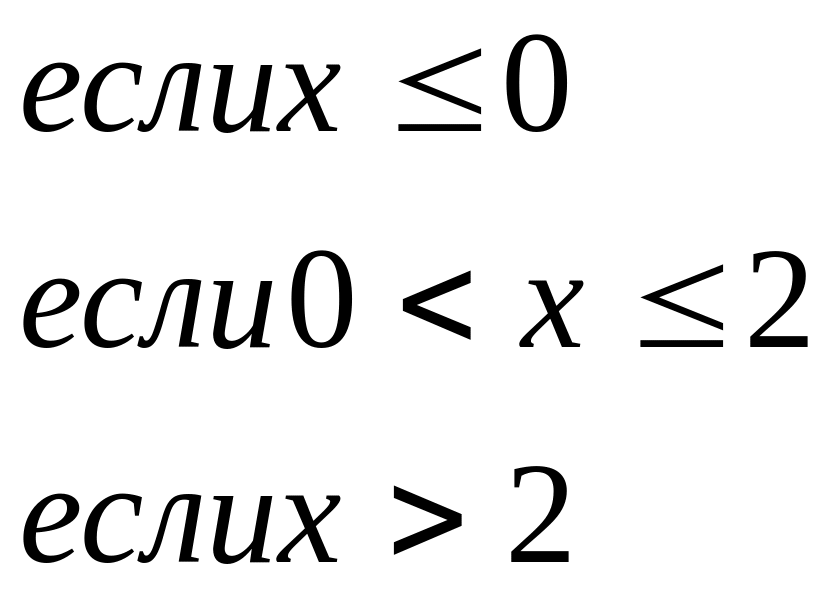
46

47

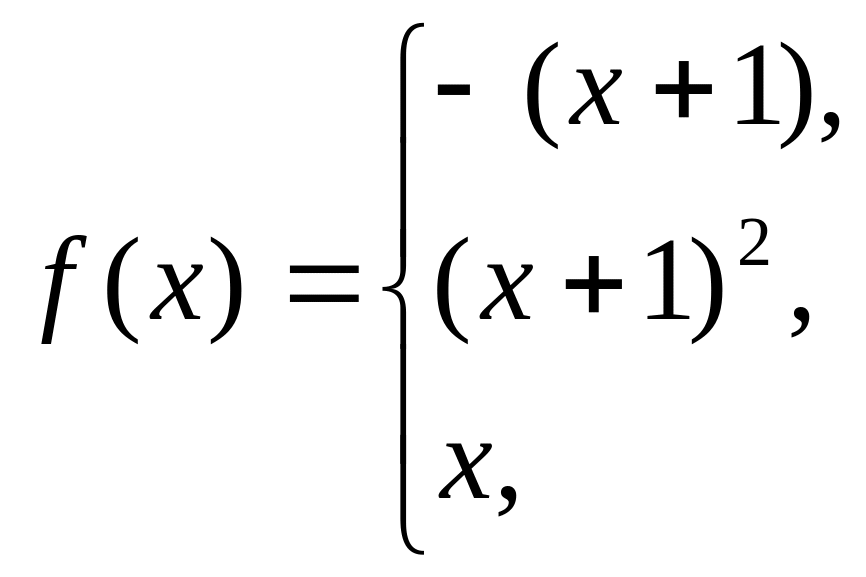
48

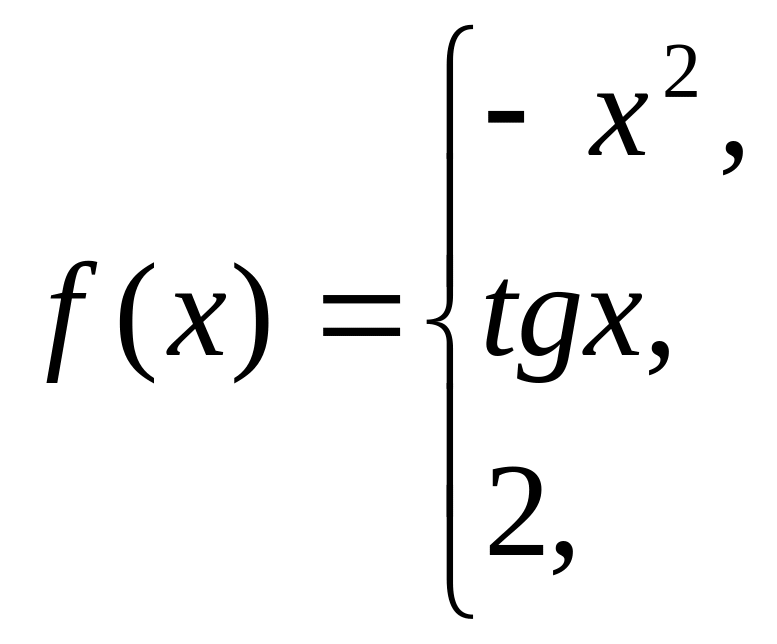
49

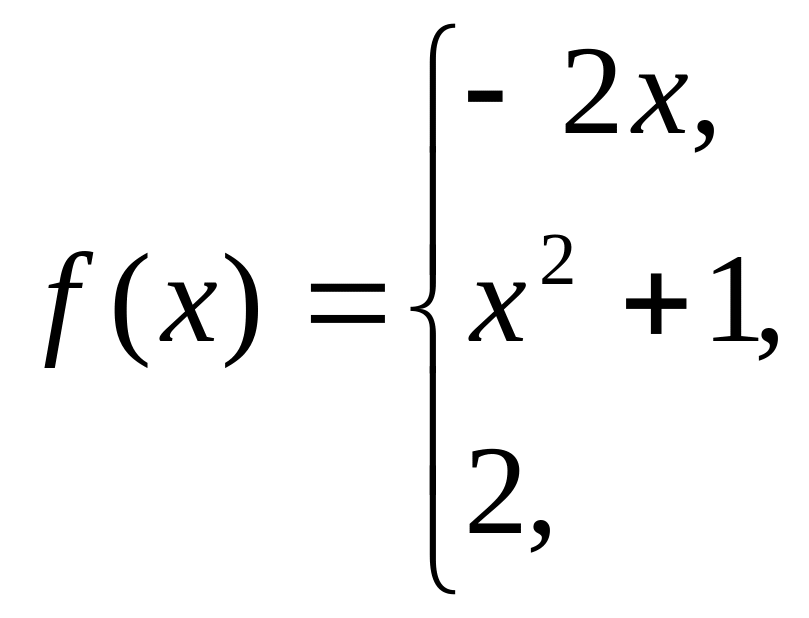
50

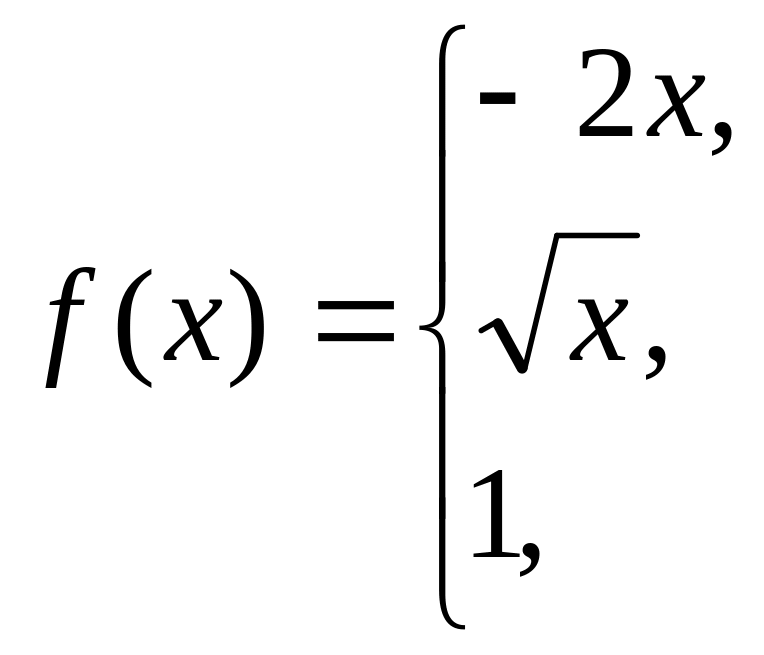
В задачах 51-70 найти производные функций.

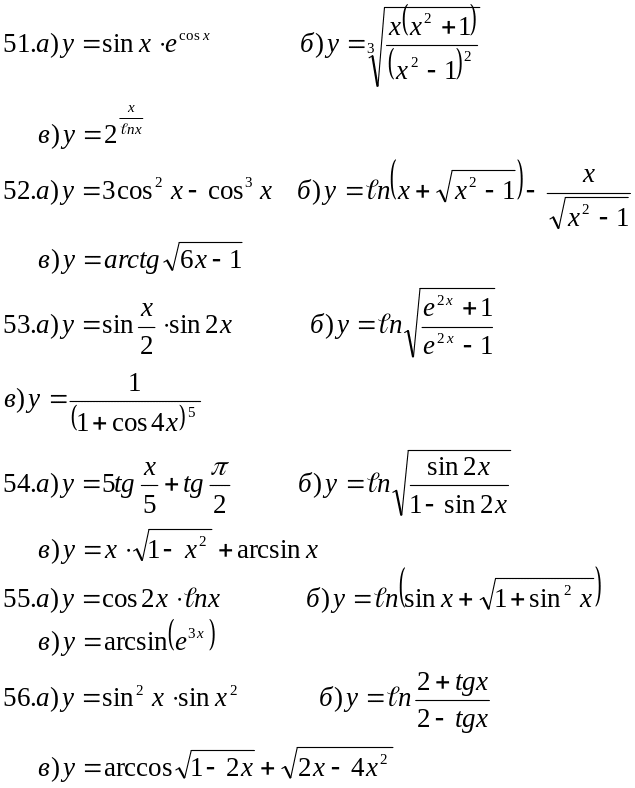
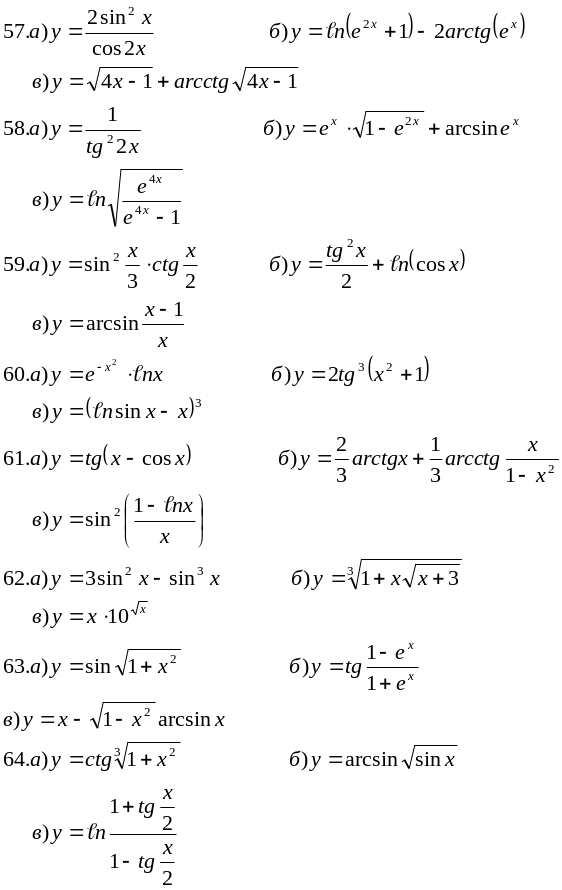
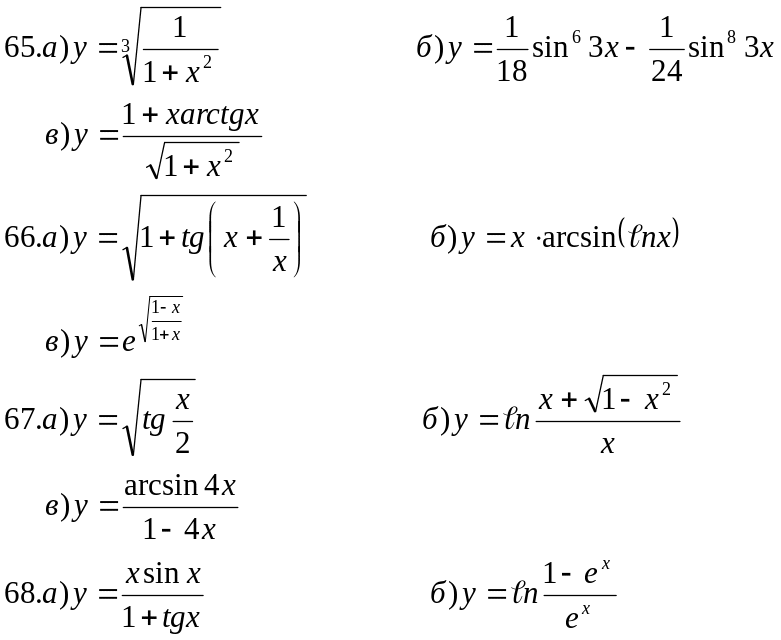
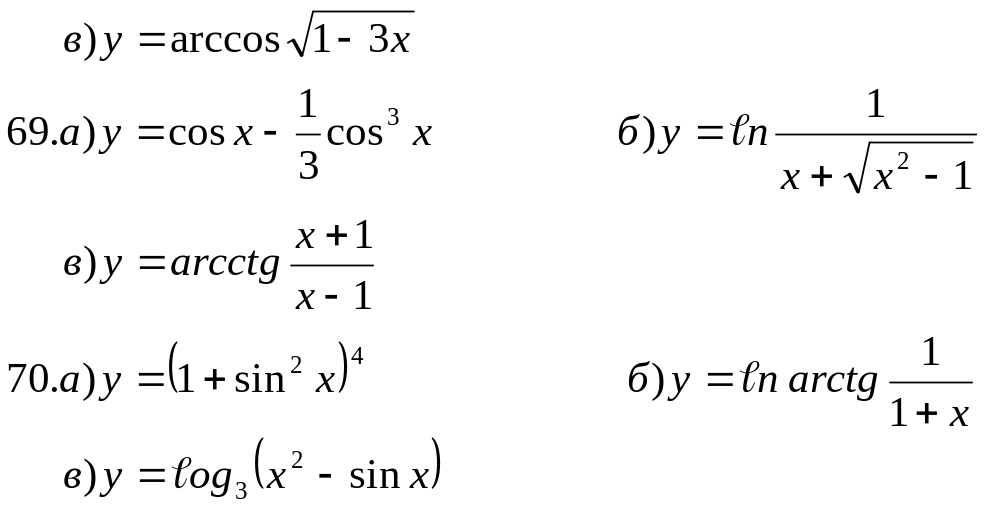
71-81 Найти наибольшее и наименьшее значения функции у = f(x) на отрезке

71

72

73

74

75

76

77

78

79

80

81 - 90. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b.

81

х	1	2	3	4	5
у	4,3	5,3	3,8	1,8	2,3

82.

х	1	2	3	4	5
у	4,5	5,5	4,0	2,0	2,5

83

х	1	2	3	4	5
у	4,7	5,7	4,2	2,2	2,7

84

х	1	2	3	4	5
у	4,9	5,9	4,4	2,4	2,9

85

х	1	2	3	4	5
у	5,1	6,1	4,6	2,6	3,1

86

х	1	2	3	4	5
у	3,9	4,9	3,4	1,4	1,9

87

х	1	2	3	4	5
у	5,2	6,2	4,7	2,7	3,2

88

х	1	2	3	4	5
у	5,5	6,5	5,0	3,0	3,5

89

х	1	2	3	4	5
у	5,7	6,7	5,2	3,2	3,7

90

х	1	2	3	4	5
у	5,9	6,9	5,4	3,4	3,9

В задачах 91-100 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить является ли данная функция четной или нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.

101. В прямой круговой конус с углом в осевом сечении и радиусом основания R вписать цилиндр с наименьшей полной поверхностью.

102. При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность?

103. В шар радиуса R вписать цилиндр наибольшего объема.

104. Найти наибольший объем конуса, образующая которого равна е.

105. Найти наименьший объем цилиндра, полная поверхность которого равна S.

106. Каковы радиус основания R и высота H открытого цилиндрического бака данного объема V, чтобы на его изготовление пошло наименьшее количество листового материала?

107. В треугольник с основанием b и высотой h вписан прямоугольник наибольшей площади Определить площадь прямоугольника.

108. Найти соотношение между радиусом R и высотой H цилиндра, имеющего при данном объеме наименьшую полную поверхность.

109. Сумма двух положительных чисел равна а. Каковы эти числа, если сумма их кубов будет наименьшей?

110. Найдите число, сумма которого со своим квадратом принимает наименьшее значение.

В задачах 111-120 найти указанные неопределенные интегралы и результат интегрирования проверить дифференцированием.

111.

112.

113.

114. ;

115. ;

116.

117.

118.

119.

120.

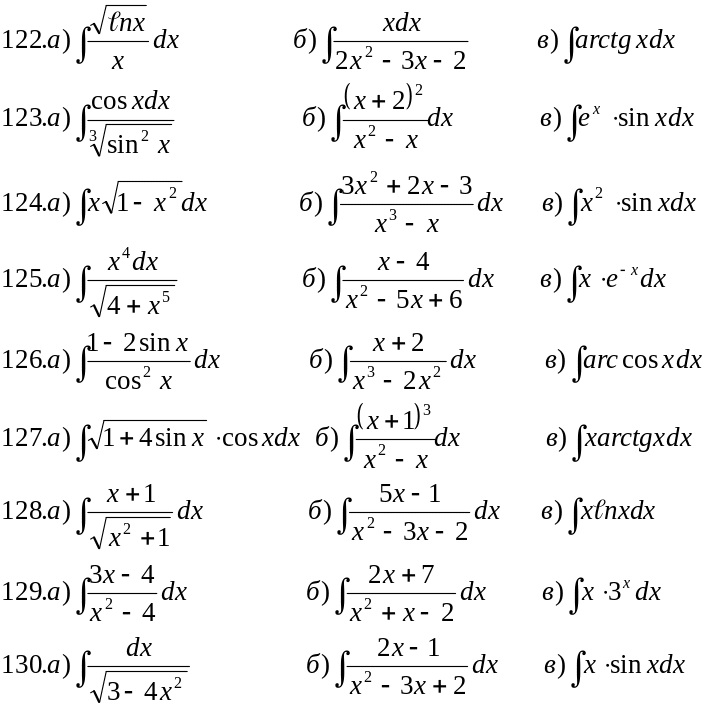
В задачах 131-140 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.

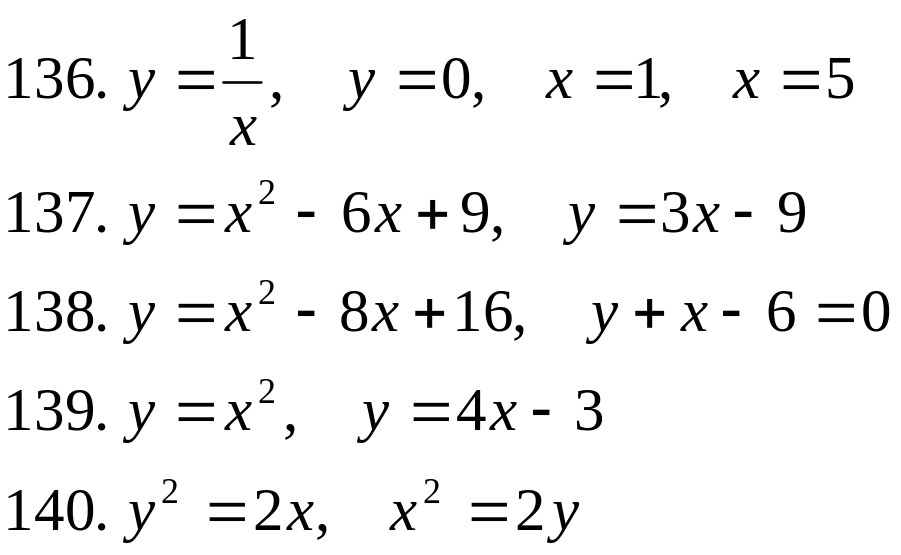
В задачах 141-145 вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж.

В задачах 146-150 вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной указанными линиями. Сделать чертеж.

151. Дана функция предельных издержек Найти функцию издержек С = С(q) и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 50 рублей.

152. Под строительство гидроэлектростанции задан непрерывный денежный поток со скоростью (млрд. руб) в течение 20 лет с годовой процентной ставкой р = 5%. Найти дисконтированную стоимость этого потока.

153. Пусть денежный поток не прекращается никогда, например, в случае эксплуатации земельного участка. Пусть (млн. рублей в год) – рента, получаемая от земельного участка, ч= 10% - процентная ставка. Найти дисконтированную стоимость земельного участка.

154. Найти дневную выработку Р за рабочий день продолжительностью 8 часов, если производительность труда в течение дня изменяется по эмпирической формуле , где t – время (час), р_о- размерность производительности, t_о- размер времени.

155. Производство оборудования некоторого вида характеризуется темпом роста его выпуска где Δу – прирост выпуска этого оборудования з промежуток времени Δt, - уровень его производства за единицу времени на момент времени t. Найти общее количество оборудования, произведенного к моменту времени t = 10 лет, получая, что К=0,05 (5% ежегодного роста) известная постоянная величина, единицей времени является год, а в начальный момент времени t = 0 уровень ежегодного производства оборудования соответствует у_о.

156. Найти объем продукции, произведенной за 4 года, если функция Кобба-Дугласа имеет вид: .

157. Определить дисконтированный доход за 3 года при процентной ставке 8%, если первоначальные капиталовложения составили 10 млн. рублей и намечается ежегодно увеличивать капиталовложения на 1 млн. рублей.

158. Производительность труда рабочего в течение дня задается функцией (ден.ед/ч), где t – время в часах от начала работы, Найти функцию , выражающую объем продукции (в стоимостном выражении) и его величину за рабочий день

159. Стоимость перевозки одной тонны груза на один километр (тариф перевозки) задана функцией (ден. ед/км). Определите затраты на перевозку 1 тонны груза на расстояние 20 км.

160. Найти среднее время, затраченное на освоение 1 изделия в период освоения от х₁=100 до х₂=121 изделий, получая в формуле (мин), b = 0,5.

161. Студент разыскивает нужную формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится:

а) только в одном справочнике;

б) только в двух справочниках;

в) во всех трех справочниках.

162. брошено три игральных кости. Найти вероятность следующих событий:

а) на каждой из выпавших граней появится 5 очков;

б) на всех выпавших гранях появится одинаковое число очков.

163. Число грузовых автомашин, проезжающих по шоссе, на которой стоит бензоколонка, относится к числу легковых, проезжающих по тому же шоссе, как 2:3. Известно, что в среднем одна из тридцати грузовых и две из пятидесяти легковых машин подъезжают к бензоколонке для заправки. Чему равна вероятность того, что:

а) к бензоколонке подъехала грузовая машина, и она будет заправляться;

б) к бензоколонке подъехала легковая машина, и она будет заправляться;

в) подъехавшая к бензоколонке машина будет заправляться.

164. В НИИ работают 120 человек, из них 70 знают английский язык, 60 – немецкий, а 50 знают оба. Какова вероятность того, что выбранный наудачу сотрудник не знает ни одного иностранного языка.

165. В первой группе студентов 15 юношей и 10 девушек, во второй – 12 юношей и 13 девушек. Из каждой группы выбирают по одному студенту. Найти вероятность того, что среди выбранных студентов хотя бы один юноша.

166. в мастерской на трех станках изготавливаются однотипные детали. Вероятность безотказной работы первого станка равна 0,8, второго – 0,7, третьего – 0,9. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,1. Найти вероятность того, что наугад выбранная деталь окажется стандартной.

167. Имеется 10 одинаковых по виду урн, из которых в 9 находятся по 2 черных и 2 белых шара, а в одной 5 белых и 1 черный шар. Из наугад взятой урны извлечен один шар. Чему равна вероятность того, что этот шар взят из урны, содержащей 5 белых шаров, если он оказался белым?

168. В урне лежит 1 шар, с равной вероятностью белый или черный. В урну положили белый шар. Шары тщательно перемешаем, затем из урны извлекли один шар. Он оказался белым. Какова вероятность того, что в урне остался белый шар.

169. В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны во вторую переложили 2 шара, а затем из второй урны наудачу извлекли один шар. Найти вероятность того, что вынутый шар окажется черным.

170. Путешественник, заблудившийся в лесу, вышел на поляну, откуда вело 5 дорог. Известно, что вероятность выхода из леса за час для различных дорог соответственно равны: 0,6; 0,3; 0,2; 0,1; 0,1. Чему равна вероятность того, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса за час?

171. В цехе 6 моторов. Для каждого мотора вероятность того, что в данный момент включен равна 0,8. Найти вероятность того, что в данный момент:

а) включено 4 мотора;

б) выключены все моторы;

в) включены все моторы;

г) включен хотя бы один мотор.

172. Монету бросают 5 раз. Найти вероятность того, что герб выпадет:

а) 3 раза;

б) не менее 3-х раз;

в) не более 3-х раз;

г) хотя бы 1 раз.

173. Для прядения смешивают поровну белый и окрашенный хлопок. Какова вероятность того, что среди 5 случайно выбранных волокон обнаружится:

а) ровно 2 окрашенных;

б) менее 2 окрашенных;

в) более 2 окрашенных;

г) хотя бы 4 окрашенных.

174. Средний процент нарушения кинескопа телевизора в течение гарантийного срока равен 12. Вычислить вероятность того, что из 10 наблюдаемых телевизоров гарантийный срок выдержат:

а) 8 телевизоров;

б) не менее 8 телевизоров;

в) хотя бы 1 телевизор.

175. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней дождливыми окажутся:

а) ровно 3 дня;

б) не более 3-х дней;

в) хотя бы 1 день.

176. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов равно 5000.

177. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность того, что в течение часа позвонят:

а) 5 абонентов;

б) хотя бы 1 абонент.

178. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Какова вероятность того, что в течение одной минуты обрыв произойдет на:

а) 5 веретенах;

б) не менее, чем на 1 веретене.

179. Производство дает 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не более 2-х.

180. Семена пшеницы содержат 0,3% сорняков. Найти вероятность того, что в 1000 семян будет:

а) ровно 5;

б) хотя бы 2 сорняка.

181. При установившемся технологическом процессе фабрика выпускает в среднем 70% продукции первого сорта. Чему равна вероятность того, что из тысячи выбранных изделий первосортных будет не менее 652 и не более 760?

182. Стрелок сделал 30 выстрелов с вероятностью попадания при отдельном выстреле 0,3. Найти вероятность того, что при этом будет 8 попаданий.

183. Посажено 600 семян кукурузы с вероятностью 0,9 прорастания для каждого семени. Найти вероятность того, что взойдет от 450 до 500 семян.

184. Приняв рождения мальчика с вероятностью 0,515, найти вероятность того, что среди 80 новорожденных 42 мальчика.

185. Было посажено 400 деревьев. Найти вероятность того, что число прижившихся деревьев более 250, если вероятность того, что отдельное дерево приживется, равна 0,8.

186.В партии смешаны детали двух сортов: 80% первого сорта и 20% второго сорта. Сколько деталей первого сорта с вероятностью 0,0967 можно ожидать среди 100 наудачу взятых деталей (выборка возвратная)?

187. Взято 800 проб руды. Вероятность промышленно содержания металла в каждой пробе одинакова и равна 0,3. Считая событие, вероятность наступления которого 0,997, достоверным, найти границы числа проб с промышленным содержанием металла во взятой партии проб.

188. Сколько семян кукурузы необходимо посеять, чтобы частность взошедших семян с вероятностью 0,99 отличалась от вероятности прорастания отдельного семени 0,95 по абсолютной величине меньше чем на 0,01?

189. Вероятность попадания в мишень при каждом из 700 выстрелов равна 0,4. Какое максимально возможное отклонение частности от вероятности попадания при отдельном выстреле можно ожидать с вероятностью 0,997?

190. Найти вероятность того, что в партии из 800 изделий отклонение числа изделий первого сорта от наивероятнейшего числа не превысит по абсолютной величине 50, если вероятность появления изделия первого сорта равна 0,7.

В задачах 191-200 задан закон распределения дискретной случайной величины Х (в первой строке указаны возможные значения величины Х, во второй строке даны вероятности р этих значений). Найти:

1. математическое ожидание М(Х);

2. 2) дисперсию D(X);

3. 3) среднее квадратическое отклонение.

191.

хi	23	25	28	29
pi	0,3	0,2	0,4	0,1

192.

хi	17	21	25	27
pi	0,2	0,4	0,3	0,1

193.

хi	24	26	28	30
pi	0,2	0,2	0,5	0,1

194.

хi	12	16	19	21
pi	0,1	0,5	0,3	0,1

195.

хi	25	27	30	32
pi	0,1	0,4	0,3	0,1

196.

хi	30	32	35	40
pi	0,1	0,5	0,2	0,2

197.

хi	12	14	16	20
pi	0,1	0,2	0,5	0,2

198.

хi	21	25	28	31
pi	0,1	0,4	0,2	0,3

199.

хi	60	64	67	70
pi	0,1	0,3	0,4	0,2

200.

хi	45	47	50	52
pi	0,2	0,4	0,3	0,1

В задачах 201-210 случайная величина Х задана интегральной функцией распределения Найти:

1. дифференциальную функцию распределения f(x);

2. математическое ожидание;

3. дисперсию.

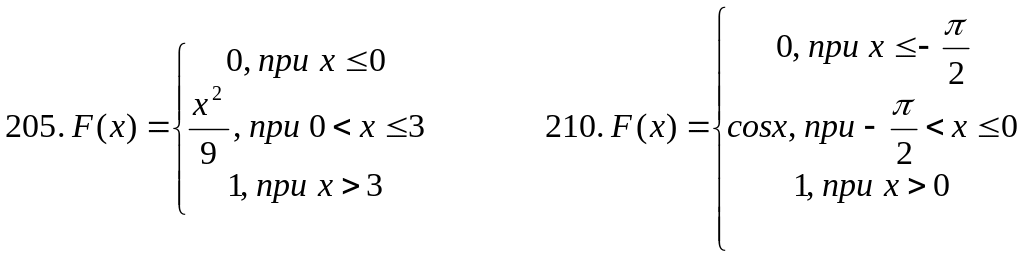
211. Масса яблока, средняя величина которой равна 150 г., является нормально распределенной случайной величиной со средним квадратическим отклонением 20г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130 г. до 180 г.?

212. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась и характеризуется средним квадратическим отклонением 0,4 мм. На сколько повысился процент бракованных деталей?

213. Случайная величина Х-масса одного зерна – распределена нормально. Математическое ожидание массы зерна равно 0,18 г. Среднее квадратическое отклонение 0,05. Хорошие всходы дают зерна, масса которых больше чем 0,15 г. Найти: а) процент семян, которых больше, чем 0,15 г;

б) величину, которую с вероятностью 0,95 не превысит масса отобранного зерна.

214. Средняя масса плодов в одном ящике равна 10 кг, а среднее квадратическое отклонение в массе плодов одного ящика 1,5 кг. Найдите: 1) вероятность события – в 100 ящиках масса плодов окажется не менее 970 кг; 2) наибольшее значение, которое с вероятностью 0,95 не превзойдет масса 100 ящиков.

Принять во внимание, что масса плодов в одном ящике – нормально распределенная случайная величина.

215.Методом проб установлено, что потери зерна при уборке в среднем составляют 3 г на м², среднее квадратическое отклонение равно 1 г. Найдите вероятность события – на 1 га потери составят не менее чем 29,8 кг. Считать, что Х-потери зерна – есть нормально распределенная случайная величина.

216. Норма высева семян на 1 га равна 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим отклонением 10 кг. Определить количество семян, обеспечивающих посев на площади 100 га с гарантией 0,95.

217. Валики, изготовленные автоматом, считаются стандартными, если отклонение диаметра валика от проектного размера не превышает 2 мм. Случайные отклонения диаметра валиков подчиняются нормальному закону со средним квадратическим отклонением δ = 1,6 мм и математическим ожиданием а = 0. сколько процентов стандартных валиков изготавливает автомат?

218. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.

219. Случайная величина распределена нормально. Среднее квадратическое отклонение этой величины равно 0,4. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет меньше 0,3.

220. Случайная величина распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 6 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (4; 8).

Задача 221-230. Колхоз имеет возможность приобрести не более а трехтонных автомашин и не более а – 2 пятитонных автомашин. Отпускная цена трехтонного грузовика – 4000 рублей, а пятитонного – 5000 рублей. Колхоз может выделить для приобретения автомашин (9а –30) тысяч рублей. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной. Задачу решить графическим и аналитическим методами. Значение параметра а даны в следующей таблице.

№ задачи	221	222	223	224	225	226	227	228	229	230
а	19	18	17	16	15	14	13	12	11	10