1. Відносність довжини (відстаней):

Довжина тіла в системі відліку, відносно якої воно знаходиться в спокої, називається власною довжиною l˳.

Лоренцове скорочення довжини – зменшення довжини в напрямку руху:

l˳= l˳√(1-v²/c²) p.s, и √(1-v²/c²) - інтеграл

При v « с маємо l= l˳ - класична механіка.

√(1-v²/c²) – кінематичний ефект.

2. Відносність проміжку часу:

Час, виміряний у системі відліку, де точки системи нерухомі, називається власним часом (t˳). Час у рухомій системі відліку:

t = t˳/√(1-v²/c²)

При v « с маємо t = t˳ - класична механіка.

Релятивістське уповільнення часу в рухомій системі відліку в

√(1-v²/c²)

експериментально підтверджено.

3. Відносність одночасності:

Події, одночасні в одній інерціальній системі відліку, не одночасні в інших інерціальних системах, рухомих відносно першої. Розрізняють події просторово-часові і причинно-наслідкові.

4. Релятивістський закон додавання швидкостей:

u = (u´+v)/(1+u´v/c²)

При u´=с, v=с, u=с.

При u´«с, v«с, u= u´+v – класична механіка.

Швидкість світла у вакуумі (с) – гранична швидкість у нашому Всесвіті.

5. Імпульс і маса тіла в ств. Другий закон Ньютона в ств.

Імпульс тіла, як і в класичній механіці, пропорційний швидкості (p=mv), де m – релятивістська маса тіла:

p=mv= m˳v/√(1-v²/c²), m=m˳/√(1-v²/c²)

При v→с m→∞.

Власна маса - m˳ (маса спокою)

Жодна частинка (тіло) з масою спокою m˳, відмінною від нуля, не може рухатися зі швидкістю, яка дорівнює и перевищує швидкість світла у вакуумі (тільки менше с).

Другий закон Ньютона в імпульсивній формі такий самий, як у класичній механіці:

F∆t = ∆p,

F∆t =∆(mv)/ √(1-v²/c²)

6. Закон взаємозв*язку маси і енергії

E=mc²

E= m˳c /√(= 1-v²/c²)

Енергія спокою тіла (власна енергія тіла) – це його внутрішня енергія.

E˳=m˳c²

Зміні енергії тіла відповідає зміна маси тіла і навпаки:

∆E˳=∆m˳c²

У релятивістській фізиці енергія тіла складається із енергії спокою тіла і його кінетичної енергії:

mc²= m˳c²+ E_к.

При зміні температури тіла змінюється його внутрішня енергія, відповідно змінюється його маса.

№50 Квантово-механічні властивості речовин.

При фізичному описі властивостей твердих тіл і встановленні залежності цих властивостей від атомно-електронної структури речовини твердого тіла широко використовуються статистичні і квантово-механічні уявлення. Тому виклад найзагальніших основ фізики твердого тіла, на яких будується сучасна електроніка, без них неможливий.

Відомості з квантової механіки і статистичної фізики, що використовуються в наступних розділах, за своїм об'ємом не виходять за рамки програми курсу загальної фізики для вищих технічних навчальних закладів. І тому наведені тут в короткій конспективній формі.

Корпускулярно-хвильовий дуалізм

У XX ст. фізики переконалися в тому, що атомні явища не можуть бути описані ні як рух частинок, ні як чисто хвильові процеси. Одні і ті ж об'єкти мікросвіту в одних умовах поводяться як частинки, в інших проявляють типово хвильові властивості. Так, в явищах дифракції, інтерференції і інших чітко виявляється хвильова природа світла. В той же час у фотоелектричних явищах, ефекті Комптона і багатьох інших світло поводиться як частинки (корпускули), що мають енергію

                         (3.1)

і імпульс

p=h/l,                              (3.2)

де — постійна Планка; .

Частинки світла одержали назву фотонів.

У 1924 р. де Бройль виcунув гіпотезу, що подвійність хвиль і корпускул, властива світлу, повинна існувати і у інших частинок – електронів, протонів, атомів і т. д. Мікрочастинці, яка має енергію Е і імпульс р, повинна відповідати хвиля з частотою

або                          (3.3)

і завдовжки

l=h/p=h/mn,                         (3.4)

де V – швидкість руху частинки. Ці хвилі називають часто хвилями де Бройля, а співвідношення (3.3) і (3.4) – співвідношеннями

де Бройля.

Гіпотеза де Бройля піддавалася ретельній багатократній перевірці і одержала таке переконливе експериментальне підтвердження, що в наш час не викликає сумнівів. На хвильових властивостях мікрочастинок грунтуються електронна мікроскопія, електронографія, нейтронографія і т.д.

Таким чином, мікрочастинка, чи то електрон, протон, атом, не є дробинкою, зменшеною до відповідних розмірів. За оберненим виразом Ланжевена, об'єктивний світ не повинен бути подібним вставним «матрьошкам» однакової форми і відмінним одна від одної тільки величиною. Перехід від об'єктів макроскопічних до об'єктів мікросвіту приводить до якісних змін, до появи нових властивостей, не властивих макроскопічним тілам. Такою новою, якісно відмінною ознакою мікрочастинок є органічне поєднання в них корпускулярних і хвильових властивостей.

№51 Невизначеність Гейзенберга і їх прикладний характер.

Принцип невизначеності є фундаментальною засадою квантової механіки, яка стверджує, що принципово неможливо одночасно виміряти з довільною точністю координати й імпульси квантового об'єкта. Це твердження справедливе не лише щодо вимірювання, а й щодо теоретичної побудови квантового стану системи. Тобто, неможливо побудувати такий квантовий стан, в якому система одночасно характеризувалася б точними значеннями координати та імпульсу.

Принцип невизначеності сформулював у 1927-му німецький фізик Вернер Гайзенберґ. Це стало важливим етапом у з'ясуванні закономірностей атомних явищ і побудови квантової механіки.

Принцип невизначеності

Загальне формулювання

Невизначеність Гайзенберґа вказує, що неможливо одночасно виміряти з довільно високою точністю координату і імпульс частинки, але аналогічна нерівність також пов'язує час і енергію, і будь-які фізичні величини, оператори яких не комутують.

У загальному випадку твердження про невизначеність значень фізичних величин та виглядає так:

,

де — середньоквадратичне відхилення від середнього фізичної величини , — середньоквадратичне відхилення від середнього фізичної величини , а — середнє значення комутатора операторів цих фізичних величин.

З цього видно, що якщо комутатор дорівнює нулю, то дану пару фізичних величин можна виміряти одночасно й точно, і, навпаки, якщо комутатор не дорівнює нулю, то фізичні величини пов'язані принципом невизначеності й одночасно визначені бути не можуть.

У граничному випадку, коли стала Планка прямує до нуля квантова механіка переходить у класичну механіку Ньютона, в якій незалежне визначення фізичних величин можливе, оскільки невизначеність стає меншою за експериментальну похибку.

№52 Рівняння Шредінгера і його використання.

№53 Рівняння обертального руху ТТ.

Робота при обертанні тіла дорівнює добутку моменту дії сили на кут повороту .Робота при обертанні тіла йде на збільшення його кінетичної енергії:

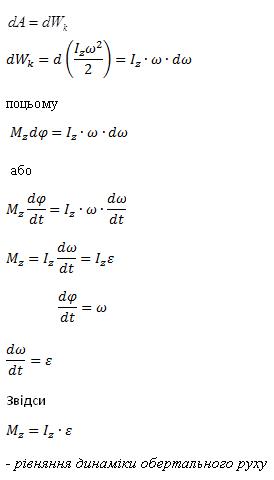
Якщо вісь обертання збігається з головною віссю інерції, що проходить через центр мас, то виконується векторна рівність

І -головний момент інерції (момент інерції щодо головної осі)

№54 Момент сили. Плече сили.

Для характеристики механічної дії на тіло, яке приводить до зміни обертального руху тіла, вводять поняття моменту сили.

Моментом сили F відносно точки О називається векторна величина М, яка дорівнює векторному добутку радіус-вектора r, проведеного з точки О в точку прикладання сили на вектор сили F: М=r*F , [M]=H*м. Напрям моменту сили визначається правилом гвинта при повороті його від r до F.

Момент сили - це вектор перпендикулярний, як до радіус-вектора точки, так і до сили, яка на цю точку діє. За абсолютною величиною момент сили дорівнює добутку сили на плече або

.

Найкоротшу відстань від точки опори до прямої, вздовж якої діє сила, називають плечем сили. Плече сили позначається літерою l та вимірюється в метрах. Для того щоб знайти плече сили, треба з точки опори опустити перпендикуляр на лінію дії сили.

№55 Правило важелів Архімеда.

У книжці «Про рівновагу і визначення центра ваги плоских фігур» Архімед уперше доводить відоме правило важеля: нерівні тягарі перебувають у рівновазі на важелі, якщо відстані центрів тягарів від точки опори важеля обернено пропорційні їх вагам. У цій самій праці Архімед визначає центри ваги прямокутників, паралелограмів, трикутників і т. д.

Є всі підстави припускати, що тут він установив саме поняття центра ваги, а не поняття центра ваги тіла: це така точка, в якій досить підтримати тіло, щоб воно було в рівновазі у будь-якому положенні.

Ва́жіль — простий механізм, тверде тіло, що може обертатися навколо певної точки, яка називається точкою опори. Застосовується для підйому вантажів.

ПРАВИЛО) Важіль знаходиться в рівновазі, тоді коли сили,що діють на нього обернено пропорційні плечам цих важелів. ( )

№56 Гідростатика. Фізичні властивості рідини.

Гідроста́тика – розділ гідромеханіки, що вивчає закони рівноваги рідини, які знаходиться у стані абсолютного чи відносного спокою та рівноваги тіл, занурених у рідини за умови, коли відсутні переміщення часток рідини одна відносно одної. У механіці не враховується молекулярна будова середовища. На певний об’єм рідини діють внутрішні і зовнішні сили. Внутрішні сили зумовлені взаємодією частинок рідини, ці сили зрівноважуються. Зовнішні сили зумовлені дією сусідніх елементів, сили тяжіння тощо. У загальному випадку рідина зазнає дії масових і поверхневих сил. Обємні сили діют на елементарні об’єми, в яких знаходиться певна маса рідини: сили тяжіння, інерції. Поверхневі сили діють на поверхню, що обмежує елементарний об’єм. При дії поверхневих сил виникають деформації об’єму, які створюють пружні сили, дія яких однакова за значенням і протилежна за напрямом дії зовнішніх сил.

Фізичні властивості рідини

Всі рідини, коли рухаються, мають внутрішнє тертя, яке обумовлене в’язкими властивостями середовища. Нехтування в’язкими силами суттєво спрощує аналітичне дослідження. Замість реальної рідини виявляється доцільним розглядати модель ідеальної рідини. Ідеальна рідина – це абстрактна рідина без внутрішніх сил тертя. В’язкість нестисливої рідини з ростом температури зменшується. Крапельна рідина приймає форму посудини і утворює поверхню вільного рівня, яка відокремлює її від других рідин або газів з іншими фізичними властивостями. На такій поверхні особливо інтенсивно проявляється дія молекулярних сил зчеплення, що призводить до появи сил капілярності, змочуваності твердих поверхонь і до виникнення крапель і менісків.

Густиною рідини r називається її маса, яка міститься в одиниці об’єму,

ρ= m/V

де m – маса рідини (кг) в об’ємі

Питомою вагою однорідної рідини називається вага G одиниці об’єму цієї рідини

γ = G/V. (1.2)

Між густиною і питомою вагою існує взаємозв’язок

Властивість рідин змінювати густину (питому вагу) при зміні температури широко використовується для створення природної циркуляції в котлах, опалювальних системах, для видалення продуктів спалювання тощо.

В’язкість рідини. Всі реальні рідини мають певну в’язкість, яка проявляється у вигляді внутрішнього тертя при відносному переміщенні суміжних частинок рідини. В’язкість рідини – це її властивість чинити опір відносному зрушенню частинок. Одиницею в’язкості в системі СІ служить паскаль-секунда.

Поверхневий натяг рідини, який зумовлений силами взаємодії молекул поверхневого шару рідини між собою намагається скоротити вільну поверхню рідини. Внаслідок цього рідина, що має криволінійну поверхню, зазнає додаткового зусилля, яке збільшує або зменшує тиск в рідині (Па). Звідси витікає закон Паскаля: тиск, що діє на рідину, передається рідиною однаково у всіх напрямках.Основне рівняння гідростатики показує, що абсолютний гідростатичний тиск в будь-якій точці простору, зайнятому рідиною, дорівнює сумі зовнішнього тиску p0 і надлишкового тиску ρgh:

.

З цього рівняння випливає рівність рівнів у сполучених посудинах, пояснення гідростатичного парадоксу та закон Архімеда

№57 Закон Паскаля.

Тиском p називають скалярну фізичну величину, що дорівнює відношенню модуля сили тиску, що діє перпендикулярно до поверхні, до площі цієї поверхні S:

У разі рівномірного розподілу сил тиску тиск на всіх ділянках поверхні однаковий і чисельно дорівнює силі тиску, що діє на поверхню одиничної площі.

У СІ за одиницю тиску взято тиск, викликаний силою 1 Н, дія якої рівномірно розподілена по перпендикулярній до неї поверхні площею 1 м2. Цю одиницю тиску називають "паскалем" (Па): 1 Па = 1 Н/м².

Тиск всередині рідини або газу вимірюють за допомогою манометрів різних типів.

Французький фізик Блез Паскаль встановив закон, який описує тиск рідин або газів. Закон Паскаля: тиск, який діє на рідину або газ в стані теплової рівноваги передається в усіх напрямах однаково.

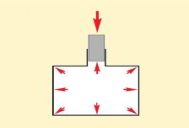
На рідину, як і на всі тіла на Землі, діє сила тяжіння. Тому кожний шар рідини, яка знаходиться в посудині, своєю вагою тисне на інші шари, і цей тиск, за законом Паскаля, передається в усіх напрямках. Тобто всередині рідини існує тиск і на одному й тому ж рівні він однаковий в усіх напрямках. З глибиною тиск рідини зростає. Так само тиск рідини залежить і від властивостей рідини, тобто від її густини.

На основі гідростатичного закону Паскаля працюють різні гідравлічні пристрої: гальмівні системи, преси тощо.

№58 Закон Архімеда.

Закон Архімеда - основний закон гідростатики, згідно з яким на будь-яке тіло, занурене в рідину або газ, діє виштовхувальна сила, яка дорівнює вазі витисненої даним тілом рідини (газу) і за напрямом протилежна їй і прикладена у центрі мас витісненого об'єму рідини. Згідно із законом Архімеда вага всякого тіла в повітрі менша за вагу його в пустоті на величину, рівну вазі витісненого повітря.

Якщо сила тяжіння тіла G більша виштовхувальної (Архімедової) сили Р, тобто G > P, то тіло тоне.

Якщо G = P, то тіло знаходиться в спокої на тій глибині, на яку воно занурено(плаває).

Якщо G< P, то тіло спливає, причому спливання припиниться тоді, коли виштовхувальна сила дорівнюватиме силі тяжіння тіла.

Сила тяжіння рідини в об'ємі рівному об’єму зануреної в неї частини тіла називається водовантажністю, а центр ваги цього об'єму – центром водовантажності.

Формула сили Архімеда

де g - прискорення вільного падіння, - густина рідини, V - витіснений об'єм.

Цей закон також допомагає пояснити поведінку тіла частково зануреного у рідину (плаваюче тіло). Тіло частково занурене у рідину має центр ваги (SC) і центр плавучості (SW). При зміні кута нахилу центр плавучості переміщається, і тіло може повернутися у вихідне положення (стабільний стан) або відхилятись повністю (нестійкий стан).

Метацентр — точка перетину осі плавання і вертикальної лінії дії виштовхуючої сили. Вісь плавання — вісь нормальна до площини плавання і проходить через центр тяжіння судна у вихідному його положенні. При невеликих відхиленнях кута положення тіла розміщення метецентру не залежить від кута. Якщо метацентр знаходиться вище від центру ваги тіла під впливом пари сил, то це заставляє тіло повернутися до вихідного стану. Якщо ж метацентр буде знаходитись нижче за центр ваги тіла, тіло продовжить відхилятись від стану рівноваги, іншими словами втратить стійкість. Відрізок від метацентру до центру ваги називається метацентричною висотою. Такі розрахунки проводяться, наприклад, при проектуванні суден.

№59 Принцип дії гідравлічного пресу.

Гідравлічний прес — це гідравлічна машина, що служить для стискування.

Сучасні гідравлічні преси можуть розвивати силу в десятки і сотні мільйонів ньютонів.

Принцип дії

Закон Паскаля дозволяє пояснити дію гідравлічної машини. Дія машини заснована на законах руху і рівноваги рідин. Основною частиною гідравлічної машини служать два циліндри різного діаметру, забезпечені поршнями і сполучені трубкою. Простір під поршнями і трубку заповнюють рідиною (зазвичай мастилом). Висоти стовпів рідини в обох циліндрах однакові, поки на поршні не діють сили. Допустимо тепер, що F1 і F2 — сили, що діють на поршні, S1 і S2 — площі поршнів. Тиск під першим (малим) поршнем рівний F1/S1, а під другим (великим) F2/S2. За законом Паскаля тиск рідини, що в усіх точках рідини у стані спокою, однаковий, тобто F1/S1=F2/S2, звідки F2/F1=S2/S1. Отже, сила F2 в стільки раз більше сили F1, в скільки разів площа великого поршня більше площі малого. Наприклад, якщо площа великого поршня 500 см2, а малого 5 см2 і на малий поршень діє сила 100 Н, то на більший поршень діятиме сила, в 100 разів більша, тобто 10 000 Н.

Таким чином, за допомогою гідравлічної машини можна малою силою зрівноважити велику силу. Відношення F2/F1 показує виграш в силі. В наведеному прикладі виграш в силі дорівнює 10000 Н/100 Н=100.

№60 Гідродинаміка. Теорема про неперервність течії.

Гідродинаміка — розділ гідромеханіки про рух нестисливих рідин під дією зовнішніх сил і механічну взаємодію між рідиною й тілами при їх відносному русі.

Рух рідин називають течією, а сукупність частинок рухомої рідини – потоком. Течію рідини називають усталеною, або стаціонарною, якщо швидкість рідини у кожній точці простору, який займає рідина, не змінюється з часом.

В гідродинаміці рівняння безперервності називають рівнянням нерозривності. Воно уособлює закон збереження маси в елементарному обсязі, тобто безперервність потоку рідини чи газу.

Для нестискувальної рідини величина в довільному перерізі однієї і тієї самої трубки повинна бути однакова:

,

Де S- площа перерізу.

Це співвідношення називається рівнянням неперервності течії. Добуток швидкості течії нестисливої рідини на площу поперечного перерізу трубки течії є величина стала для даної трубки течії. Трубка течії – це частина рідини, обмежена лініями течії. Всі частинки, що містяться всередині трубки течії, не виходять за межі трубки і жодна з частинок, що знаходяться за межами, не проникає в неї.

№ 61 Рівняння Бернуллі та його наслідки.

Рівняння Бернуллі — рівняння гідродинаміки, яке визначає зв'язок між швидкістю течії v, тиском p та висотою h певної точки в ідеальній рідині.

p — статичний тиск; - динамічний тиск; hρg - гідростатичний тиск.

Рівняння Бернуллі можна сформулювати так: в стаціонарному потоці ідеальної нестискуваної рідини сума статичного, динамічного і гідростатичного тисків є сталою на довільному поперечному перерізі потоку.

Для трубки течії, яка розміщена горизонтально ( ), рівняння Бернуллі має такий вигляд:

,

де називається повним тиском.

Із рівняння Бернуллі для горизонтальної трубки течії видно, що при течії рідини в горизонтальній трубці, що має різні перерізи, швидкість рідини більша в місцях звуження трубки, а тиск більший в місцях, де площа поперечного перерізу трубки більша.

Рівняння Бернуллі є наслідком закону збереження енергії. Якщо рідина не ідеальна, то її механічна енергія розсіюється і тиск вздовж трубопроводу, яким тече така рідина, спадає.

Рівняння Бернуллі широко застосовують для розв'язання багатьох гідравлічних задач у нафтогазовій справі.

Наслідки з рівняння Бернуллі

1.Якщо потік горизонтальний, то рівняння набуває вигляду:

Звідси видно, що там, де швидкість потоку більша, тиск менший і навпаки. Зокрема в трубці змінного перерізу, коли рідина переходить з ширшої частини трубки у вужчу, збільшення швидкості супроводжується зменшенням тиску.

Ця різниця тисків визначає прискорюючи силу, що діє на одиницю площі потоку рідини.

2. Значне зниження тиску в швидких струминах рідин або газів використовують для побудови водоструминних, ртутних або масляних насосів, інжекторів, пульверизаторів тощо.

3.Трубка Піто – прилад для вимірювання швидкості потоку рідини або газу. Прилад має дві трубки – одну з отвором проти потоку і другу з отвором, паралельним потоку. Застосовуючи рівняння Бернуллі для положень частинок потоку в отворах трубок, дістанемо:

Складову називають динамічним тиском, а - статистичним.

№62 Підйомна сила крила.

Підіймальна сила — складова аеродинамічної сили, перпендикулярна вектору швидкості руху тіла в потоці рідини або газу, на відміну від паралельної складової — аеродинамічного опору. Підіймальна сила виникає внаслідок несиметричності обтікання тіла потоком. Відповідно до закону Бернуллі, статичний тиск середовища в тих місцях, де швидкість потоку вища, буде нижчим, і навпаки. Ця різниця тисків і породжує підіймальну силу.

Повна аеродинамічна сила — це інтеграл від тиску навколо контуру крила.

де:

• Y — підіймальна сила

• P — тяга,

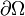•  — межа профілю,

• p — тиск,

• n — нормаль до профілю

За теоремою Жуковського, розмір підіймальної сили пропорційний густині середовища, швидкості потоку і циркуляції швидкості потоку.

Коефіцієнт підіймальної сили — безрозмірна величина, що характеризує підіймальну силу крила певного профілю при відомому куті атаки. Коефіцієнт визначається експериментально в аеродинамічній трубі, або за теоремою Жуковського. Формулу розрахунку підіймальної сили через коефіцієнт розробили брати Райт і Джон Смітон на початку XX століття. Формула має вигляд:

де:

• Y — підіймальна сили (Н)

• C y — коефіцієнт підіймальної сили

• ρ — густина повітря на висоті польоту (кг/м³)

• V — швидкість набігаючого потоку (м/с)

• S — характерна площа (м²)

При розрахунках за цією формулою важливо не плутати вагову і масову щільність повітря. Вагова щільність при стандартних атмосферних умовах (на рівні землі при температурі +15 С) дорівнює   = 1.225 кг / м ^3. Але в аеродинамічних розрахунках часто використовують масову щільність повітря, яка дорівнює 0.125 кг * с² / м ^4. В цьому випадку підйомна сила Y виходить не в ньютонах (Н), а в кілограмах (кг). У книгах з аеродинаміки не завжди є уточнення, про яку щільності і розмірності підйомної сили йде мова, тому в спірних ситуаціях потрібно перевіряти формули, скорочуючи одиниці виміру.

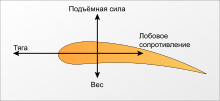
Чотири сили, що діють на літак

№63 Рух реальної рідини. Сили внутрішнього тертя, коефіцієнт в'яз­кості.

Реальна рідина - модель природної рідини, що характеризується ізотропністю всіх фізичних властивостей, але на відміну від ідеальної моделі, володіє внутрішнім тертям при русі.При вивченні руху реальної (в'язкої рідини) можна піти двома різними шляхами: скористатися готовими диференціальними рівняннями і їхніми рішеннями, отриманими для ідеальної рідини. рівняння Бернуллі для елементарної струминки реальної рідини має вигляд:

де   і   - питомі енергії положення, що характеризують потенційну енергію в перерізах 1-1 і 2-2;

 і   - питомі енергії тиску, що характеризують потенційну енергію тиску в тих же перерізах;

 і   - питомі кінетичні енергії у тих же перерізах;

• - втрати питомої енергії.

Внутрішнє тертя – це явище виникнення сил тертя між шарами одного газу або рідини, котрі рухаються один відносно другого паралельно з різними швидкостями.

Дане явище описує закон Ньютона

F = -η(Δu/Δz)

де F -  сила внутрішнього тертя, яка діє на одиницю площі поверхні прошарку, Δu/Δz – градієнт швидкості напрямленого руху молекул газу. Як відомо реальна рідина відрізняється від ідеальної наявністю в'язкості, тобто між окремими шарами рідини при русі існує тертя. Так як існує тертя, то повинні з'явитися і втрати енергії. Тобто частина енергії реальної рідини, що рухається переходить в тепло. Відбувається так звана дисипація Причому цей перехід енергії є незворотним. У зв'язку з цим  можна вважати втраченою питомою енергією.Рідини характеризуються в'язкістю. Вона визначається як здатність чинити опір переміщенню однієї з частини рідини відносно іншої, тобто як внутрішнє тертя.В’язкість рідин – це результат взаємодії внутрішньомолекулярних силових полів, що перешкоджають відносному рухові двох шарів рідини. Отже для переміщення шару один відносно одного треба подолати їх взаємне притягання, причому чим воно більше, тим більша потрібна сила зсуву. При відносному зсуві шарів у газовому середовищі, в результаті перенесення молекулами газу кількості руху під час їх переходу з шару в шар, виникає дотична сила між шарами, що протидіє проковзуванню останніх.Таким чином, внутрішнє тертя в рідині, на відміну від газів, зумовлене не обміном молекул, а їх взаємним притяганням. Доказом цього є те, що із збільшенням температури, як відомо, обмін молекул зростає і тертя в газах зростає, а в рідинах спадає у зв'язку із послабленням міжмолекулярного притягання.Коефіцієнт   називають динамічний коефіцієнт в’язкості або абсолютною в'язкістю. Одиниця вимірювання динамічного коефіцієнта в'язкості  — Па c, Пуаз (0,1Па·с).Кількісно динамічний коефіцієнт в'язкості дорівнює силі F, яку треба прикласти до одиниці площі зсувної поверхні шару S, щоб підтримати в цьому шарі ламінарну течію із сталою одиничною швидкістю відносного зсуву.Виділяють також кінематичний коефіцієнт в’язкості ν, що є відношенням динамічного коефіцієнта в'язкості до питомої маси речовини

.

Одиниця вимірювання кінематичного коефіцієнта в'язкості  — Стокс, м²/с. Коефіцієнт ν на відміну від η виражається величинами, які не пов’язані з масою рідини, тобто величинами, які носять, так би мовити, кінематичний характер, у той час як η носить динамічний характер.

№64 Рух рідини по трубах. Пропускна спроможність труб.

Якщо рідина нерухома, то тиск у точках, розташованих на одному рівні, однаковий. З глибиною тиск зростає. Обчислити його можна як добуток густини рідини, глибини та прискорення вільного падіння.Рух рідини по трубах часто зустрічається в техніці та побуті. Тиск у рідині, яка рухається, залежить від площі поперечного перерізу.Закон Бернуллі визначає залежність тиску від швидкості руху в трубах різного поперечного руху: при протіканні однорідної нестисливої нев’язкої рідини через трубу змінного перерізу тиск буде більшим там, де швидкість протікання менша, і навпаки.При рівномірному русі величина середньої швидкості і розподілення швидкості по перерізу повинні залишатися незмінними по довжині трубопроводу. Тому рівномірний рух можливий лише в трубах сталого перерізу, коли при заданій витраті крапельної рідини Q середня швидкість буде незмінною  . Рівномірний рух має місце в прямих трубах або в трубах з дуже великим радіусом кривизни    (прямолінійний рух), так як в іншому разі середня швидкість змінюється по напрямку. Нарешті, умова незмінності по довжині труби характеру розподілу швидкості по живому перерізу можна записати у вигляді a  =  const, де a  – коефіцієнт Коріоліса.    (4.1) або (4.2) де Т – дотичні сили опору;  – дотичне напруження на стінці труби, Па ;  – “змочений периметр” живого перерізу потоку в трубі геометричним радіусом   ;  – повна поверхня, де проявляються дотичні сили опору,   ;  – площа живого перерізу труби,   – тиск відповідно в перерізі 1 і 2 , Па.

Втрати енергії (зменшення гідравлічного напору) у трубопроводі можна спостерігати в рідини, що рухається не тільки на довгих ділянках, але й на коротких. В одних випадках втрати напору розподіляються (іноді рівномірно) по довжині трубопроводу — це лінійні втрати; в інших — вони зосереджені на дуже коротких ділянках, довжиною яких можна знехтувати, на так званих місцевих гідравлічних опорах: вентилях, поворотах і заокругленнях, звуженнях, розширеннях, розгалуженнях і т.д., тобто скрізь, де потік деформується. Причиною втрат в обох випадках є в'язкість рідини і втрачена енергія розсіюється у вигляді тепла.

Пропускна здатність взагалі, є метричною характеристикою, яка дозволяє показувати й розраховувати співвідношення граничного обсягу (в нашому випадку рідини) за одиницю певного часу через трубу. Адже на відміну від сталевих труб, пластикові труби не заростають зсередини і не схильні внутрішньої корозії. Відповідно і канали в таких трубах не забиваються природними відкладеннями, а їх пропускна здатність залишається в рамках норми. Пропускна здатність сталевої труби з часом змінюється в гіршу сторону.Але, крім обліку пропускної спроможності за обсягом переміщуваного речовини, нам необхідно знати яка пропускна здатність водопровідної труби до розрахунку підключення всіх сантехнічних приладів і обладнання в будинку. Хоча б для того, щоб включаючи кран у кухні, ви були впевнені, що у ванній кімнаті не припиниться подача води.

№65 Визначення коефіцієнту в'язкості.

Визначення коефіцієнта в’язкості за допомогою формули Пуазейля. Вона встановлює зв’язок між об’ємом газу, що протікає за одиницю часу через переріз труби і різницею тисків, необхідною для цього :

,

де  діаметр труби,  її довжина. Вимірявши об’єм, різницю тисків та знаючи геометричні розміри труби, можна визначити коефіцієнт в’язкості.

Метод вимірювання коефіцієнта в’язкості, який ґрунтується на використанні формули Пуазейля, часто називають капілярним методом, а відповідні прилади — капілярними віскозиметрами. Для течії в циліндричній трубі (капілярі) перехід до турбулентного руху відбувається, коли безрозмірна величина   стає більшою, ніж деяке критичне значення, порядку 1000. Тут ρ — густина газу;   — середня швидкість течії; r — радіус труби; η— в’язкість газу. Ця величина називається числом Рейнольдса (звідси і позначення Rе). Якщо число Рейнольдса менше від критичного значення, то рух ламінарний, а якщо перевищує його — турбулентний. 

№66Ламінарна та турбулентна течія. Число Рейнольда. Умови ламі-нарності течії.

Ламіна́рна течія́ — впорядкований рух рідини або газу, при якому рідина (газ) рухається шарами, паралельними до напрямку течії.Ламінарна течія — рух частинок по паралельних лініях з певною малою швидкістю. Характерна для течії підземних вод.

Режим течії рідини характеризується числом Рейнольдса

Re = ρvl/µ,

де ρ — густина,

µ — коефіцієнт динамічної в'язкості,

v — характерна швидкість течії рідини (газу),

l — характерний розмір.

Ламінарна течія має місце, коли число Re менше від критичного значення. Для випадку течії води в круглій трубі Re_кр = 2200. Ламінарна течія спостерігається в дуже в'язких рідинах або при течіях з досить малими швидкостями, а також при повільному обтіканні дуже в'язкою рідиною тіл малих розмірів. Із збільшенням швидкості руху даної рідини (газу) ламінарна течія переходить у турбулентну течію.

Турбулентним називається рух рідини (газу або плазми), що супроводжується утворенням вихорів.Течія, що відбувається без утворення вихорів, називається ламінарною.Критерієм турбулентності є число Рейнольдса:

Re = ρvl/µ,

де ρ — густина,

µ — коефіцієнт динамічної в'язкості,

v — характерна швидкість течії рідини (газу),

l — характерний розмір.

При малих значеннях числа Рейнольдса добуток характерної для течії швидкості плину на характерні розміри перешкод малий в порівнянні із в'язкістю. Тому завдяки в'язкості течія зберігає впорядковану структуру. При великих значеннях числа Рейнольдса рух рідини стає турбулентним.Турбулентна течія має місце, коли число Re більше від критичного значення. Для випадку течії води в круглій трубі Re_кр = 2200. 

Число Рейнольдса( ) — характеристичне число та критерій подібності у гідродинаміці, що базується на відношенні інертності руху течії флюїда до його в'язкості.

Позначається Re, іноді R.

,

де:  ,

Використані позначення фізичних величин:

 — густина рідини або газу.

 — характеристична швидкість,

 — характеристична довжина або розмір,

 — динамічна в'язкість,

 — кінематична в'язкість,

 Це число також використовується для характеристики різних режимів: ламінарної або турбулентної течії. Ламінарна течія спостерігається при малих числах Рейнольдса, де сили в'язкості переважають, і вона характеризується сталістю розподілу швидкості руху рідини. Турбулентний режим спостерігається при великих числах Рейнольдса, коли переважають сили інерції, котрі, як правило, спричиняють хаотичні вихори та іншу нестабільність потоку.

№67 Предмет дослідження молекулярної фізики. Будова речовин. Ви­значення вуглецевих одиниць.

Розділ фізики, в якому вивчаються будова, фізичні властивості і агрегатні стани речовини на основі їхньої мікроскопічної (молекулярної) будови, називається молекулярною фізикою. В основі молекулярної фізики лежать підтверджені теоретично і експериментально положення, що речовини складається з молекул або атомів, які перебувають у безперервному русі і взаємодіють між собою. Основні положення МКТ речовини:

· 1. Будь-які речовини мають дискретну (переривчасту) будову. Вони складаються з найдрібніших частинок молекул і атомів. Підтвердженням дискретності є прокатка, кування металу, отримання 1974 року фотографії окремих молекул і атомів, розчинність речовин тощо. Молекули - найменші частинки, які мають хімічні властивості речовини. Молекули складаються з більш простих частинок - атомів хімічних елементів. У природі є 92 хімічні елементи. Разом із штучними наразі налічується 105 елементів.

Речовину, яка побудована з атомів лише одного виду, називають елементом (водень, кисень, азот тощо). Кожен елемент має свій номер Z в таблиці Менделєєва. Число Z визначає кількість протонів у ядрах атомів і електронів, що рухаються в атомі навколо ядра.

· 2. Молекули знаходяться в стані неперервного хаотичного (невпорядкованого) руху, що називається тепловим і у загальному випадку є сукупністю поступального, обертального і коливального рухів.

Під час нагрівання речовини швидкість теплового руху і кінетична енергія його частинок збільшуються, а під час охолодження зменшуються. Ступінь нагрітості тіла характеризує його температура, яка є мірою середньої кінетичної енергії хаотичного поступального руху молекул цього тіла.

· 3. Молекули взаємодіють одна з одною із силами електромагнітної природи, причому на великих відстанях вони притягуються, а на малих - відштовхуються. Сили притягання і відштовхування між молекулами діють постійно.

Вуглецева одиниця, уніфікована атомна одиниця маси, складова маси атома ізотопу вуглецю 12 C.

В. е. була запропонована в 1959 Міжнародним союзом теоретичної і прикладної хімії (IUPAC), прийнята в 1960 Міжнародним союзом теоретичної і прикладної фізики (IUPAP) і затверджена на конгресі IUPAC в 1961. В. е. рівна (1,66043 ± 0,00031)×10 -24 р

№68 Моль речовини. Число Авогадро. Характерний розмір молекул.

Моль — одиниця кількості речовини в системі СІ. Позначається моль, Mol. Інша назва — грам-молекула.

Кількість речовини, що містить число Авогадро ( ) структурних формульних одиниць. Формульні одиниці — реальні частки, такі як атоми, молекули, іони, радикали.

За формальним означенням моль — це кількість речовини, виражена в грамах, що чисельно дорівнює її молекулярній масі і відзначається тим, що одному молю будь-якої речовини відповідає однакова кількість молекул. А саме, 1 моль містить стільки молекул (атомів, йонів, інших структурних елементів речовини), скільки атомів у 0,012 кг вуглецю 12С, тобто дорівнює сталій Авоґадро.

Позначення «Моль» введене у 1893 році Вільгельмом Оствальдом і походить від слова «молекула».

Прості молекули, наприклад молекули більшості газів, складаються з двох-трьох атомів. А у деяких газів, таких як гелій і неон, – взагалі з одного. Однак існують і такі, які мають у своєму складі тисячі атомів, з'єднаних один з одним в складній послідовності. Часто буває, що молекули містять кілька однакових атомів. Наприклад, молекула води складається з двох атомів водню і одного – кисню.

Молекула чистого природного каучуку, з якого отримують гуму, складається приблизно з 75 000 атомів вуглецю і 100 000 атомів водню. Так що, як бачите, молекули різних речовин сильно відрізняються за своєю величиною.Так, розмір молекули води вимірюється мільярдними частками сантиметри. Молекула гуми в тисячі разів більше. Форма молекул може бути так же самій різною: одні з них згорнуті в клубочок, нагадує футбольний м'яч, а інші представляють собою довгі нитки. Практично неможливо наочно уявити собі справжні розміри молекул.

№69 Температура. Визначення температури газовим термометром.

Температура – скалярна фізична величина, яка окреслює здатність макроскопічної системи (тіла), що знаходиться в стані термодинамічної рівноваги, до теплопередачі- фіз. величина, що характеризує ступінь нагрівання тіла – це відображення інтенсивності руху молекул. Температура характеризує ступінь нагрітості тіла. Поняття температури може бути введено на основі різних підходів: як величина, пропорційна середній кінетичній енергії частинок тіла, як розподіл частинок тіла за рівнями енергії або за швидкостями, за ступенем іонізації, за спектральною густиною випромінювання та ін. Такі температури часто називають відповідно температурами збудження, кінематичною, іонізаційною, радіаційною. Газовий термометр, прилад для виміру температури, дія якого заснована на залежності тиску або об'єму ідеального газу від температури. Найчастіше застосовують Р. т. постійного об'єму ,який є заповненим газом балоном 1 незмінного об'єму, сполучений тонкою трубкою 2 з пристроєм 3 для виміру тиску. У такому Р. т. зміна температури газу в балоні пропорційно зміні тиску. Р. т. вимірюють температури в інтервалі від ~2К до 1300 К. Градус Цельсія (°C) — одиниця виміру температури, подібна до Кельвіна. Широко використовується в побуті. За нуль за шкалою Цельсія приймалася точка плавлення льоду, а за 100 градусів — точка кипіння води при стандартному атмосферному тиску.

№70 Шкала Цельсія та абсолютна шкала температури.

Шкала Цельсія, шкала температур, в основу якої покладено температури замерзання (0 ° С) і кипіння (100 ° С) води. Інтервал між цими двома значеннями розділений на 100 градусів. Назва шкали (по імені її винахідника Андерса Цельсія) було офіційно закріплено в 1948 р., замінивши собою колишню назву «стоградусной». Градуси Цельсія переводяться в градуси Фаренгейта допомогою множення на 1,8 і додавання 32.

Абсолю́тна температу́рна шкала́, шкала́ Ке́львіна — температурна шкала, в якій початковою точкою є абсолютний нуль, а одиницею температури — градус, що дорівнює градусові за шкалою Цельсія.

Співвідношення між Т (температурою за абсолютною шкалою) і t (температурою за шкалою Цельсія) виражається формулою:

Т = t + 273.16 °C

Одиницею температури в абсолютній температурній шкалі є Кельвін.

№71 Рівняння Клапейрона.

Рівняння Клапейрона- Мендєлєєва – це рівняння стану ідеального газу для його довільної маси. Воно звучить так: при сталій кількості речовини ідеального газу добуток його тиску на об’єм прямо пропорційний абсолютній температурі.

або p₂V₂=BТ₂.

Це рівняння було виведене Клапейроном. В – питома газова стала, яка залежить від роду газу і його кількості. Мендєлєєв надав рівнянню більш зручного для користування вигляду, скориставшись законом Авогадро. Завдяки цьому стала в рівнянні газового стану, розрахована на 1 моль речовини, буде дорівнювати: R=8,31 Дж/моль*К – універсальна газова стала. Звідси рівняння стану, розрахованого на 1 моль газу: pV=RT – рівняння Клапейрона-Мендєлєєва. Для будь-якої маси m газу рівняння Клапейрона-Мендєлєєва записується так:

№72 Ізопроцеси. Закон Бойля-Маріотта.

Де μ – маса, яку має моль газу.

Якщо в газі відбуваються якісь процеси, то звичайно змінюються всі три його параметри: р, V і Т

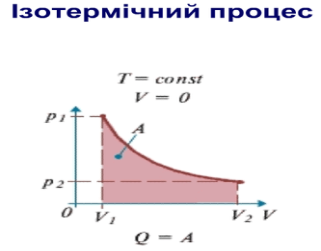
Ізотермічний процес. Якщо в рівнянні вважати Т - const, права частина рівняння буде величиною сталою:

pV= const.

Закон Бойля—Маріотта, або рівняння стану ідеального газу при ізотермічному процесі, означає: добуток тиску даної маси газу на об'єм, що його займає газ за сталої температури, є величиною сталою Графічно залежність між тиском і об'ємом газу за сталої температури зображають гіперболою. Ці криві називають ізотермами (кривими однакових температур). Чим вища температура, за якої відбувається процес, тим вище розташована ізотерма (Т₁ <Т₂< Т₃). pV = const

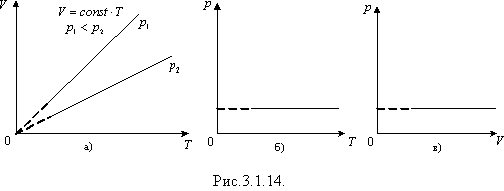Ізобарний процес. Нехай тепер газ знаходиться в умовах, коли сталим є його тиск р. З рівняння Клапейрона випливає, що в цьому випадку сталим буде відношення об'єму газу до його температури

= const,

тобто за незмінної маси газу і сталого тиску об'єм газу прямо пропорційний абсолютній температурі.

Перехід газу з одного стану в інший за сталого тиску називають ізобарним процесом. Графічно такий процес в координатних осях V, Т зображується прямою, продовження якої проходить через початок координат,— ізобарою. Кут її нахилу а до осі температур залежить від тиску газу: чим більший тиск, тим менший кут нахилу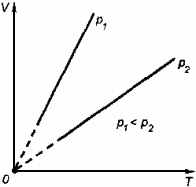

Ізохорний процес. Розглянемо випадок, коли об'єм V газу залишається сталим. З рівняння Клапейрона випливає, що за цих умов сталим буде відношення тиску газу до його температури:

тобто за сталого об'єму тиск газу прямо пропорційний його абсолютній температурі

Перехід газу з одного стану в інший за сталого об'єму називають ізохорним процесом. Графік цього процесу в координатах р, Т — пряма лінія, продовження якої проходить через початок координат ; її називають ізохорою. Кут нахилу а ізохори до осі температур тим більший, чим менший об'єм газу.

t˚C; α- коефіцієнт об’ємного розширення газу. Придосить низьких тисках величина α є однаковою для різних газів.

α = 0,003661 К^-1

№73 Закон Гей-Люссака.

Ізобарний процес відбувається в системі при сталому тиску (р=const). Такий процес можна здійснити, коли газ, наприклад, міститься в циліндрі з рухомим поршнем.зміна температури такого газу в такому циліндрі зумовлює переміщення поршня, тобто зміну об’єму. Тиск при цьому залишається сталим. При р=const V/T=const - ізобарного процесу (закон Гей-Люссака). Закон Гей-Люссака записують у вигляді V=V₀(1+αt), де V₀– об’єм газу при 0˚С; V- об’єм газу при температурі

V=V0 (1+ α t);

V=V0 α T

№74 Закон Шарля.

Ізохорний процес відбувається при сталому об’ємі газу (V=const). при V=const р/ V=const.- це рівняння називається рівнянням ізохорного процесу. Рівняння ізохорного процесу записують у вигляді р=р₀(1+βt), де p₀ і p –т иски при 0˚С і t˚C; β – термічний коефіцієнт тиску (β=0,003661).

Рівняння показує, що в ізохоричному процесі тиск газу перебуває в лінійній залежності від температури. Температуру, при якій тиск газу дорівнює нулю, називають абсолютним нулем.

p = p0 (1+ α t);

p = p0 α T

№75 Парціальний тиск. Закон Дальтона.

Парціа́льний тиск - внесок газу певного роду в загальний тиск суміші газів.

Згідно із законом Дальтона у випадку ідеальних газів парціальні тиски окремих компонент суміші газів сумуються

Парціальний тиск кожної із компонент, пропорційний долі цієї компоненти в суміші газів.

P_i = x_iP,

де

,

ν_i - кількість молів i-го газу в суміші, ν - загальна кількість молів газу.

Парціальні тиски кожної з компонент можуть бути розраховані, використовуючи рівняння стану, таким чином приведена формула задає рівняння стану суміші.

Закон Дальтона – загальний тиск P суміші ідеальних газів дорівнює сумі парціальних тисків Pi компонентів у суміші:

Джон Дальтон встановив цей закон емпірично в 1801. Закон справедливий для газів, близьких до ідеальних. В реальних газах, для яких суттєва взаємодія між молекулами суміші, можуть існувати суттєві відхилення від такого простого правила.

Випаровування над водною поверхнею визначають за допомогою емпіричних формул, одержаних при використанні закону Дальтона.

№76 Молекулярно-кінетична теорія газового тиску.

Кінетична теорія або молекулярно-кінетична теорія - фізична теорія, що пояснює термодинамічні явища, виходячи з атомістських уявлень. Теорія постулює, що тепло є наслідком хаотчиного руху надзвичайно великої кількості мікроскопічних частинок (атомів та молекул). В сучасній фізиці молекулярно-кінетична теорія розглядається як складова частина статистичної механіки.

Молекулярно-кінетична теорія виходить із того, що речовина, зокрема газ складається з великої кількості мікроскопічних частинок (молекул), які рухаються хаотично. Частинки стикаються між собою та зі стінками посудини, створюючи на ці стінки тиск. Усі зіткнення вважаються пружними, тобто проходять без втрати енергії. Середня кінетична енергія руху частинок залежить від температури.

Середня кінетична енергія руху молекули

,

де m - маса частинки, v - її швидкість, k_B - стала Больцмана, T - температура.

Середня швидкість частинок у газі дорівнює

,

де R - газова стала, M - молярна маса.

Тиск газу на стінки посудини визначається з того міркування, що при пружньому відбитті частинки від стінки, зміна її імпульсу дорівнює 2mvx, де vx - перпендикулярна до стінки складова швидкості. Підрахувавши переданий за час Δt імпульс, і прирівнявши його до імпульсу сили для тиску отримуємо

,

де n - кількість частинок в одиничному об'ємі.

№77 Розподіл середньої енергії молекул за ступенями вільності.

Для того, щоб визначити енергію, яка припадає на всі рухи молекул, необхідно ввести поняття про число ступенів вільності.

Числом ступенів вільності називають найменше число координат, які необхідно задати для того, щоб повністю визначити положення тіла у просторі, або кількість незалежних рухів, які може виконувати тіло.

У класичній статистичній фізиці виводиться закон Больцмана про рівно­мірний розподіл енергій за ступенями вільності молекул:

Для статистичної системи, що перебуває у стані термодинамічної рівноваги, на кожний поступальний і обертальний ступінь вільності припадає в середньому кінетична енергія, що дорівнює , а на кожний коливальний ступінь вільності – в середньому енергія .

Коливальний ступінь має вдвоє більшу енергію тому, що на нього припадає не лише кінетична енергія, але і потенціальна енергія, причому середні зна­чення кінетичної і потенціальної енергій однакові:

.

Таким чином, середня енергія молекули

,

де .

Важливою характеристикою термодинамічної системи є її внутрішня енергія

U – енергія хаотичного (теплового) руху мікрочастинок системи (молекул, атомів, електронів, ядер і тощо) і енергія взаємодії цих частинок.

Внутрішня енергія – однозначна функція термодинамічного стану системи, тобто в кожному стані система має цілком визначене значення внутрішньої енергії.

В ідеальному газі немає сил взаємодії між молекулами, а, отже, дорівнює нулю взаємна потенціальна енергія молекул. Тому для моля ідеального газу внутрішня енергія дорівнює сумі кінетичних енергій молекул:

.

Якщо є молів газу, то його внутрішня енергія

.

Внутрішня енергія ідеального газу залежить від кількості ступенів вільності молекул і абсолютної температури газу.

№78 Внутрішня енергія ідеального газу.

Внутрішньою енергією називається сума кінетичної і потенціальної енергії всіх молекул речовини.

Кінетична енергія – це енергія руху, а потенціальна – це енергія взаємодії.

Оскільки в ідеальному газі відсутні сили взаємодії, то це означає, що молекулярно-потенціальна енергія у нього відсутня. Таким чином внутрішня енергія ідеального газу представляє собою тільки суму значень кінетичних енергій хаотичного руху всіх його молекул.

Для одного моля внутрішня енергія буде виражена формулою:

А для довільної маси одноатомного газу:

- для двохатомного газу

- для багатоатомного газу

№79 Нульове начало термодинаміки Вчення про тепло.

Нульовий закон термодинаміки - теорема, яка формулюється наступним чином: якщо дві системи знаходяться в стані тепловой рівноваги з третьою системою, то вони знаходяться в стані тепловой рівноваги і між собою. Очевидно, що стан тепловой рівноваги є ніщо інше, як рівність температур.

Нульовий початок термодинаміки був так названий за пропозицією англійського фізика Р. Фавлера (1889-1944).

Умовою рівноваги між системами або частинками є умова рівності їх температур(і це твердження не залежить від виду обраного термометра). Температура – характеристика стану теплової рівноваги. Функція, що зв’язує тиск, об’єм і температуру фізично однорідної системи, яка перебуває в термодинамічній рівновазі називається рівнянням стану.

№80Перше начало термодинаміки. Його застосування до ізопроцесів.

Зміна внутрішньої енергії може відбуватися за рахунок двох різних процесів: виконання над тілом роботи А та передачі йому деякої кількості теплоти Q.

Перший початок термодинаміки формулюється так: кількість теплоти, надана тілу, витрачається на збільшення його внутрішньої енергії та на виконання тілом роботи над зовнішніми тілами (зовнішнім середовищем): . Перший початок термодинаміки у диференціальній формі записується так: , де - елементарна кількість теплоти, dU- диференціал внутрішньої енергії, - елементарна робота. Не можливо побудувати машину, що діє періодично, яка виконувала б роботу без одержання енергії ззовні або виконувала б більшу роботу, ніж одержана ззовні енергія. Це є друге формулювання першого закону термодинаміки.

Створення або зникнення енергії є не можливим. Це є третє формулювання першого закону термодинаміки. Цим формулюванням фіксується взаємоперетворення видів енергії.

ЗАСТОСУВАННЯ ЗАКОНУ

-при ізохорному процесі енергія, яку отримує тіло шляхом теплообміну іде на збільшення його внутрішньої енергії

-при ізотермічному процесі уся підведена до тіла к-ть теплоти іде на виконання тілом роботи

-при ізобарному процесі кількість теплоти переданій системі іде на збільшення внутрішньої енергії системи та на виконання нею роботи

p=const A=pΔV

№81 Друге начало термодинаміки.

Створити вічний двигун першого роду неможливо.

Ентропія –тепловий хаос, чим більш хаотична система в середині, тим більш стабільна ззовні.

1.1824 – вперше подано ідею другого начала С. Карно

2.1850 – Р. Клаузіус : неможна передати енергію від менш

нагрітого тіла до більш нагрітого

3.1851 – У. Томсон : не можна побудувати машину, що діє

періодично, яка б перетворювала теплоту в енергію тільки в наслідок

охолодження одного тіла, без того,щоб у навколишніх тілах не відбувалось жодної зміни

4.1853 – В. Освальд : не можна створити вічний двигун другого роду .

№82 Третє начало термодинаміки.

dS = d'Q / T ентропія ( перетворення, зміна) вперше

введена Клаузіусом у 1854 році.

!Абсолютний нуль температур досягти неможливо.

Ср і Сv, термічні коефіцієнти теплового розширення та тиску прямують до нуля.

Термодинамічна шкала температур є незалежною від виробу термодинамічного тіла, встановлюється на основі теореми і циклу Карно.

№83Робота газу при сталому тиску.

Зміна енергії тіла відбувається тільки при виконанні механічної роботи або при теплообміні. Закон збереження енергії є першим началом термодинаміки.

Підведення до системи кількість теплоти Q частково іде на збільшення внутрішньої енергії системи і частково на виконання цією системою роботи

Вигляд цього рівняння для ізобаричного процесу:

збільшується об’єм і підвищується температура

Процес в якій-небудь системі, що відбувається без теплообміну з оточуючим середовищем називається адіабатним процесом.

, тоді

З цього випливає, що під час адіабатного процесу система може виконувати роботу тільки за рахунок зменшення своєї внутрішньої енергії.

№84Теплоємність газу за сталого об'єму та сталого тиску.

Кількість теплоти поглинутої тілом при зміні його стану залежить не лише від його початкового та кінцевого станів, зокрема, від його початкової та кінцевої температури, але і від способу, в який було здійснено перехід від початкового до кінцевого стану. Відповідно від цього залежить і теплоємність тіла. Звичайно, розрізняють теплоємність за сталого тиску C_P і теплоємність за сталого об`єму C<sub>V</sub>, якщо в процесі нагрівання підтримують, відповідно, сталий тиск Р або сталий об`єм V. При нагріванні за сталого об’єму (V=const, ізохоричний процес) уся підведена до тіла теплота йде на збільшення його внутрішньої енергії, тоді як при нагріванні за сталого тиску (P=const, ізобаричний процес) на збільшення внутрішньої енергії тіла йде лише частина підведеної до тіла теплоти, оскільки інша частина йде на виконання роботи розширення тіла. Отже, C_P завжди більше за C_V. Для твердих тіл і рідин різниця між C_P та C_V незначна, оскільки зміни їх об’єму при нагріванні невеликі. Знання  є важливим, оскільки безпосереднє вимірювання C_V становить значні експериментальні труднощі (при V=const маса газу, а отже його теплоємніcть завжди малі порівняно з відповідними величинами для калориметра), і теплоємність C_V звичайно обчислюють за формулою C_V  = C_P/ , оскільки вимірювати C_P значно зручніше.

C_P - C_V = R,

де R – універсальна газова стала, що дорівнює 8,314 Дж/(моль∙K) . Відповідно до класичної теорії теплоємності ідеальних газів для одноатомного газу теплоємність C_V = 3R/2, для газу, що складається із двоатомних молекул, C_V =5R/2, а для ідеального газу багатоатомних жорстких молекул C_V =6R/2.

Якщо газ можна вважати ідеальним, то за відомим відношенням молярних теплоємностей γ можна навіть знайти їх абсолютні величини. Можна знайти самі теплоємності C_V = R/( –1) та   C_P = R/( –1).

№85 Закон Дюлонга та Пті.

Зако́н Дюлонга — Пті визначає питому теплоємність твердого тіла за формулою

де c — питома теплоємність, R — універсальна газова стала, M — молярна маса.

Закон Дюлонга—Пті справедливий при температурах вищих за температуру Дебая.

Питома теплоємність – характеристика речовини, яка вказує кількість теплоти, необхідної для нагрівання одиниці маси речовини на 1градус C, або ж кількість теплоти, що виділяється при охолодженні одиниці маси речовини. Відкритий закон був у 1819році.

Фізична природа

Для того, щоб підвищити температуру потрібно збільшити кінетичну енергію руху кожного із атомів твердого тіла. Однак, внаслідок сильної взаємодії атомів між собою, збільшення кінетичної енергії потребує рівного за величиною збільшення потенціальної енергії. Тому теплоємність твердого тіла вдвічі більша за теплоємність ідеального газу. Закон Дюлонга—Пті можна переписати для теплоємності твердого тіла у вигляді:

,

де С — теплоємність, — стала Больцмана, N — число атомів у кристалі.

Теплоємність – це фізична величина, яка визначається кількістю теплоти, яку потрібно надати тілу для підвищення його температури на один градус.

Для справедливості закону Дюлонга-Пті необхідно, щоб енергії теплового руху вистачало для збудження всіх можливих типів коливань у твердому тілі. При низьких температурах деякі з коливань не збуджуються. Це явище зумовлене законами квантової статистики (в даному випадку — статистики Бозе-Ейнштейна). Тому при низьких температурах закон Дюлонга-Пті не діє.

Як було встановлено П.Л. Дюлонгом і А.Г. Пті, молярна теплоємкість твердих одноатомних тіл майже однакова і дорівнює:

де R= 8,31 – універсальна газова стала.

Закон Дюлонга і Пті є дійсним для твердих одноатомних тіл для достатньо високих температур. Для більшості тіл такою високою температурою є вже кімнатна температура.

Для деяких тіл з малою атомною масою, наприклад, берилію, бора, вуглецю (структури алмазу), молярну теплоємкість можна визначити і при високих температурах за законом Дюлонга і Пті. Навпаки, при охолоджені, для всіх тіл закон Дюлонга і Пті не дає точне визначення молярної теплоємкості, тобто, є відходження від закону.

№86 Барометрична формула.

Барометри́чна фо́рмула— формула, за якою визначають залежність тиску або густини газу від висоти. Ця залежність зумовлена дією поля тяжіння Землі і тепловим рухом молекул газу (повітря). Припускаючи, що газ є ідеальним газом сталої температури, і вважаючи поле тяжіння Землі однорідним, отримують барометричну формулу такого вигляду:

,

де p0 — тиск на нульовому рівні (на рівні вибою в газових свердловинах, біля поверхні Землі або на рівні моря), Па;

p — тиск на висоті h, м над цією поверхнею, Па;

m — маса молекули (для повітря дорівнює масі молекули азоту), кг;

g — прискорення вільного падіння, м/с2;

k — стала Больцмана, Дж/К;

T — абсолютна температура повітря, К.

Барометрична формула є наближеною: при виведенні її не враховано залежності g i T від висоти, відхилення газу від ідеального газу тощо. Нею можна користуватися для визначення атмосферного тиску до висоти 11 км (з поправками на зміну температури). За уточненою барометричною формулою градуюють альтиметри, висотоміри. Зміну тиску нерухомого стовпа газу у свердловині розраховують за уточненою барометричною формулою Лапласа-Бабіне:

,

де p(z) — тиск газу на глибині z, м, Па;

p0 — тиск газу на гирлі свердловини, Па;

Γ — відносна густина газу (до повітря);

Tс — середня температура газу, К;

zΓ — середній коефіцієнт стисливості газу при середньому тиску і середній температурі газу.

Барометричну формулу з певним обмеженням можна використати для визначення розподілу кількості колоїдних частинок по висоті рідинної або газової дисперсної системи, на які діє поле тяжіння. Барометрична формула є окремим випадком розподілу Больцмана.

№87 Адіабатичний процес. Рівняння адіабати.

Адіаба́тний проце́с — в термодинаміці зміна стану тіла без обміну теплом з навколишнім середовищем. Його можна здійснити, проводячи стискання чи розширення тіла (наприклад, газу) дуже швидко. Так, при поширенні звукових хвиль у повітрі чи іншому тілі, у місцях згущення частинок температура підвищується, а в місцях розрідження — знижується. За дуже малий період коливання не відбувається помітного обміну теплом між місцями згущення і розрідження.

Під час адіабатного стискування тіла внутрішня енергія його збільшується, а при адіабатичному розширенні — зменшується. Виконана робота при цьому дорівнює за величиною і протилежна за знаком зміні внутрішньої енергії системи.

Математично адіабатичний процес описується рівнянням

де P — тиск, V — об’єм,

C_P — молярна теплоємність за умов постійного тиску, а C_V — молярна теплоємність за умов постійного об'єму. Для одноатомного ідеального газу, γ = 5 / 3, а для двоатомного (таких як азот або кисень, головних складових повітря) γ = 1.4. Ця формула може бути застосована лише для класичних газів.

Для адіабатичного процесу теплообмін з навколишнім середовищем відсутній, тобто кількість теплоти Q = 0. Тоді, відповідно до першого закону термодинаміки,

№88 Цикл Карно. Коефіцієнт корисної дії теплової машини.

машина – це періодично діючий пристрій, який може виконувати механічну роботу за рахунок внутрішньої енергії палива. У тепловому двигуні робоче тіло (пара, газ) отримує від нагрівника з температурою T₁ (палива, що згоряє) певну кількість теплоти Q₁ і, здійснюючи цикл, виконує роботу A та віддає холодильнику (довкіллю) з температурою T₂ кількість теплоти Q_2.

Цикл Карно́ — цикл роботи теплового двигуна.

Цикл складається з чотирьох стадій:

1)Робоча речовина нагрівається за сталої температури (ізотермічний процес).

2)Робоча речовина розширюється за сталої ентропії (адіабатичний процес).

3)Робоча речовина охолоджується за сталої температури (ізотермічний процес).

4)Робоча речовина стискається за сталої ентропії (адіабатичний процес).

Коефіцієнт корисної дії для двигуна, що працює за циклом Карно, залежить лише від різниці температур нагрівача T₁ і охолоджувача T₂. η = T₁ -T₂/ T₁

Карно сформулював наступну теорему: всі оборотні двигуни, що працюють між двома термостатами, мають той самий ККД; жоден необоротний двигун, що працює між тими ж термостатами, не може мати більш високого ККД. У реальних двигунах ККД завжди трохи нижче, ніж ККД ідеального двигуна.

При роботі теплової машини робоче тіло здійснює замкнутий термодинамічний цикл. Для будь-якої реальної теплової машини весь цикл, включаючи його окремі процеси, незворотній, що викликає необхідність витрачати частину виробленої роботи для перекладу робочого тіла в первинний стан, забезпечуючи замикання кругового процесу. Зазначені втрати призводять до того, що не вся вироблена робота стає корисною, а частина її втрачається в самій теплової машині, переходячи в теплоту. Максимальним к.к.д. володіє теплова машина, в якій цикл робочого тіла складається тільки з рівноважних теплових процесів, і, отже, є оборотним. Однак для здійснення нагрівання й охолодження необхідний теплообмін робочого тіла з нагрівачем і холодильником теплової машини, який тим більш ефективний, ніж помітніше різниця температур. Виникаючі при цьому теплові потоки порушують стан теплової рівноваги і роблять ці процеси незворотними. Щоб уникнути цього, необхідно теплообмін здійснювати при дуже малій різниці температур, в межі, для досягнення рівноважного процесу, при нескінченно малій різниці. Тому реалізувати рівноважний процес при теплообміні можна тільки в разі теплового рівноваги робочого тіла і нагрівача (або холодильника).

Теплообмін з нагрівачем і холодильником в розглянутій теплової машині повинен відбуватися при ізотермічних процесах.

Така умова може бути виконано тільки приблизно. Інший процес, який може протікати без виникнення теплових потоків - це адіабатичний процес. Якщо він протікає нескінченно повільно, то такий процес є рівноважним і оборотним. Зазначені два рівноважних процесу (ізотермічний і адіабатичний) можуть бути використані для складання оборотного циклу. Для організації найпростішого кругового процесу досить використання двох ізотерм і двох адіабати. Такий рівноважний термодинамічний цикл отримав назву циклу Карно.. Оборотний цикл Карно складається з двох ізотерм, що описують процес теплопередачі від нагрівача до робочого тіла і від робочого тіла до холодильника, і двох адіабати, що описують розширення і стиснення робочого тіла в тепловій машині .

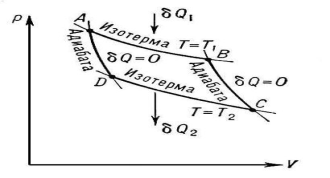
Цикл Карно на діаграмі: Р – тиск, V – об'єм.

Тіла, які зовні здаються твердими, не завжди є такими з точки зору фізики. Істинно тверді тіла мають кристалічну структуру, з упорядкованістю молекул чи атомів у межах всього кристалу (з дальнім порядком). При нагріванні кристалічної речовини зростає хаотичність руху її молекул, і за досить високої температури зникає дальній порядок (відбувається процес плавлення). Хімічно прості кристали плавляться за цілком визначеної температури. Зворотний процес — тверднення (кристалізація). Температура кристалізації збігається з температурою плавлення. Від початку плавлення (і тверднення) і до закінчення кожного з цих процесів температура речовини залишається незмінною.

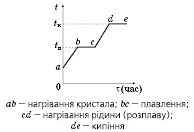
Чим більша маса речовини, яку треба розплавити, тим більша кількість теплоти для цього потрібна: ,  ,  , .

№89 Теплові властивості реальних середовищ. Температурна діаграма процесу нагрівання речовини.

Температура характеризує величину нагрівання тіла і визначає напрямок передачі теплоти. Якщо , то теплота переходить від тіла А до тіла В. При цьому температура тіла А зменшується, а температура тіла В збільшується. Якщо , то самовільного переходу теплового потоку між ними не буде.

Числове значення термодинамічної абсолютної температури можна визначити з рівняння у вигляді:

.

Таким чином, у термодинаміці температура розглядається як середньостатистична величина, що характеризує систему, яка складається з величезного (але кінечного) числа молекул, які знаходяться у хаотичному (тепловому) русі.

У технічній термодинаміці в якості робочого тіла розглядається ідеальний газ - теоретична модель реального газу, в якій не враховується взаємодія часток газу, молекул, що являють собою безоб’ємні матеріальні точки; силами міжмолекулярного зчеплення зневажають. Це дає підставу кожен дійсно існуючий у природі газ, в якому можна знехтувати силами зчеплення та об'ємом молекул (через малу їх величину), називати ідеальним газом. Ця обставина тим більш справедлива, чим вище температура газу і менше тиск.

№90 Питома теплота плавлення та пароутворення речовини.

Питома теплота плавлення  чисельно дорівнює кількості теплоти, яку необхідно передати одному кілограму кристалічної речовини, нагрітої до температури плавлення, щоб перетворити її на рідину тієї ж температури. Для процесу кристалізації  ; у цьому випадку   — питома теплота кристалізації. 

Вимірюється в (Дж/кг)

Питóма теплотá випарóвування (пароутворення) — це фізична скалярна величина L, що чисельно дорівнює кількості теплоти, яку необхідно надати 1 кг рідини для перетворення її в пару при температурі її кипіння. Одиниці вимірювання в СІ - джоуль на кілограм ([L] = Дж/кг).

Отже:  ,  ,  , .

Питома теплота випаровування дорівнює питомій теплоті конденсації, тобто кількості теплоти, яка виділяється при конденсації 1 кг газу при сталій температурі.

Для процесу конденсації  ; у цьому випадку L — питома теплота конденсації. 

№91 Рівняння Ван-дер-Ваальса. Ізотерми Ван-дер-Ваальса.

Для дослідження поведінки одного моля реального газу розглянемо ізотерми Ван- дер-Ваальса, які визначаються рівнянням:

Перетворимо це рівняння у вигляд:

і

де а – поправка, що залежить від інтенсивності молекулярних взаємодій; b – поправка, що зумовлюється розмірами молекул газу; p – внутрішній тиск; V_m- молярний об’єм газу; R=8,31 Дж/моль*К – універсальна газова стала.

Коефіцієнти рівняння залежать від тиску, температури і хімічної природи газу. Ізотерми газу, які описуються рівнянням Ван-дер-Ваальса, мають вигляд, наведений на рис. 66, де .

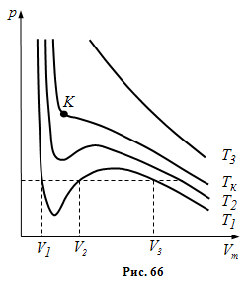
При температурах є область станів, де кожному значенню тиску відповідають три точки ізотерми й ізотерма має хвилеподібну ділянку. При підвищенні температури ці три точки зближуються і зливаються в одну точку К , яка є точкою перегину ізотерми при Дотична до ізотерми в точці К паралельна осі абсцис. При температурах ізотерми Ван-дер-Ваальса близькі до ізотерми ідеального газу.

Розглянемо ізотерми при (рис. 67). На ділянках 1-3 і 5-7 при зменшенні об’єму зростає тиск р що відповідає експерименту. Частина ізотерми 1-2 відповідає газоподібному стану, а частина 6-7 – рідині.

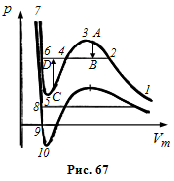
На ділянці стискання речовини приводить до зменшення тиску . У природі немає і не може бути таких речовин, в яких із збільшенням тиску об’єм не зменшується, а зростає. Стан речовини з такими властивостями повинен бути дуже нестійким.

Істинна ізотерма матиме вигляд ламаної лінії . У станах, що відповідають горизонтальній ділянці 2-6 , спостерігається рівновага рідкої і газоподібної фази речовини.

№92 Класифікація матеріалів за електричними властивостями. Провід­ники, діелектрики, напівпровідники та надпровідники.

До провідників належать речовини, які мають вільні заряджені частинки, що здатні рухатись впорядковано по всьому об'єму тіла під дією електричного поля. Це пояснюється тим, що валентні електрони легко віддаляються від атомів. Якщо металевий провідник внести в електричне поле, то під впливом електричних сил вільні електрони перерозподіляються. Перерозподіл зарядів триватиме доти, поик напруженість поля всередині провідника не дорівнюватиме нулю. Провідниками є всі метали, деякі хімічні сполуки, водні розчини солей, кислот, лугів, розплави солей, іонізовані гази.

Власні напівпровідники зазвичай мають невелику концентрацію вільних носіїв заряду, електронів та дірок, яка залежить від ширини забороненої зони та температури. При збільшенні температури концентрація вільних електронів та дірок дуже швидко зростає. Ефект цього зростання набагато перевищує ефект від збільшення частоти актів розсіяння, тож провідність власних напівпровідників різко збільшується при високих температурах. Іншим фактором, який збільшує провідність власних напівпровідників, є створення підвищеної концентрації вільних носіїв заряду світловим опроміненням або інжекцією. При поглинанні кванта світла в напівпровіднику утворюється пара носіїв заряду - електрон переходить із валентної зони у зону провідності, залишаючи за собою дірку. Якщо до освітленого напівпровідника прикласти напругу, то в напівпровіднику потече доволі значний струм. Така провідність називається фотопровідністю і широко використовується у різноманітних фотоелементах. Аналогічну провідність можна створити при опроміненні швидкими частками, що служить основою роботи напівпровідникових детекторів радіації.

У легованих напівпровідниках навіть при кімнатних температурах концентрація електронів у зоні провідності (напівпровідники n-типу) чи дірок у валентній зоні (напівпровідники p-типу) висока, оскільки для переходу між зоною й домішковим рівнем електрону потрібно набрати набагато меншу енергію (глибина домішкових рівнів зазвичай не перевищує 0.5 еВ). Тому провідність легованих напівпровідників доволі висока й наближається до провідності металів. Вона теж росте із температурою, оскільки для неї фактор збільшення концентрації носіїв у зоні важливіший за збільшення частоти актів розсіяння. Контакти між областями n-типу й p-типу, які називають p-n переходами мають особливу односторонню провідність. На цьому факті базується робота різноманітних напівпровідникових пристроїв - діодів, транзисторів, фотодіодів, напівпровідникових сонячних елементів, активного шару копіювальних машин, лазерних принтерів тощо.

Надпровідники можуть нескінченно довго підтримувати електричний струм навіть, коли електричне поле, яке його викликало, виключити. Формально провідність напівпровідників нескінченна. Надпровідний стан існує лише при низьких температурах, хоча теоретично верхня границя температури переходу із надпровідного в звичайний стан не встановлена.

Фізична природа нескінченної провідності надпровідників в тому, що в надпровідниках подавлені канали розсіяння енергії. Носіями заряду в надпровідниках є куперівські пари - зв'язані стани двох електронів із протилежними спінами й протилежними напрямками руху. Куперівські пари утворюються завдяки непрямому притягуванню між електронами, зумовленому взаємодією із кристалічною ґраткою. Електрон, рухаючись в кристалі, деформує ґратку, створюючи «канал», який притягає інший електрон. Куперівські пари мають унікальні властивості. У них неможливо забрати енергію, бо електрони, які увійшли до їх складу, вже віддали енергію на утворення пари.

Діелектрик або ізолятор складається з нейтральних атомів або молекул. Електрони і ядра в нейтральному атомі зв”язані між собою і не можуть переміщатися під дією поля по всьому об”єму тіла, як вільні заряди провідника. Всередині діелектрика може існувати електричне поле.

Додатній заряд зосереджений в центрі атома. Електрон рухається навколо ядра з великою швидкістю: один оберт за 10 ^–15 с. Це дає підставу вважати, що центр розподілу від”ємного заряду припадає на середину атома, тобто збігається з додатньо зарядженим ядром.

Електричним диполем наз. нейтральну в цілому систему двох однакових за модулем і протилежних за знаком точкових зарядів, що перебувають на де-якій відстані один від одного.

Отже, діелектрики можна поділити на такі види:

• Неполярні – що складаються з атомів або молекул, у яких центри розподілу додатніх і від”ємних зарядів збігаються (інертні гази, кисень, водень).

• Полярні – що складаються з молекул, у яких центри розподілу додатніх і від”ємних зарядів не збігаються (спирт, вода, сіль,…).

В полярному діелектрику тепловий рух зумовлює хаотичну орієнтацію електричних диполів. На поверхні і в об”ємі діелектрика електричний заряд рівний нулю. І напруженість електричного поля рівна нулю.

В неполярному діелектрику під дією поля молекули деформуються і їх можна розглядати як пружні електричні диполі.

Отже, діелектрик, вміщений в електричне поле, поляризується.

Електричне поле поляризаційних зарядів завжди спрямоване назустріч зовнішньому полю, тому зовнішнє поле всередині діелектрика послаблюється (але не компенсується повністю, як у провідниках), а поблизу діелектрика поле спотворюється.

Зв’язаний заряд створює в діелектрику електричне поле Е₁, що спрямоване проти напруженості зовнішнього поля зарядів на пластинах Е₀. Через це поле всередині діелектрика послаблюється. Напруженість результуючого поля становить:

Е = Е₀ – Е₁.

Для характеристики електричних властивостей діелектрика вводять фізичну величину – діелектричну проникливість.

Діелектрична проникливість середовища – це фізична величина, що показує, у скільки разів модуль напруженості електричного поля Е всередині діелектрика менший за модуль напруженості поля Е₀ у вакуумі:

Напруженість електричного поля точкового заряду або зарядженої кулі, які вміщені в однорідний діелектрик:

Закон Кулона для зарядів в однорідному діелектрику:

№93 Капілярні явища. Сила поверхневого натягу, висота підняття рі­дини в капілярі.

КАПІЛЯРНІ ЯВИЩА - поверхневі явища на межі рідини і твердого тіла, що стикаються між собою; викликані, головним чином, дією сил поверхневого натягу; напр., піднімання або опускання рівня рідини (і утворення меніска) у тонких трубках, занурених у рідину, на яку діє сила ваги; завдяки капілярним явищам відбувається рух соків у рослинах, води у ґрунті.

К апілярний ефект - явище підвищення або зниження рівня рідини у капілярах в порівнянні з тим значенням, яке вимагає закон сполучених посудин.

Капілярний ефект виникає через зниження або збільшення тиску рідини під меніском, який утворюється при змочуванні рідиною стінок капіляра.

Величина підвищення або зниження h залежить від радіуса капіляра r, а також від кута змочування рідиною стінок θ

,

де γ - коефіцієнт поверхневого натягу рідини, ρ - густина рідини, g - прискорення вільного падіння.

Приклад капілярного ефекту - всмоктування пролитої води серветкою.

Найбільш характерною властивістю рідини, що відрізняє її від газу, є те, що на межі з газом рідина утворює вільну поверхню. На кожну молекулу рідини діють сили притягання сусідніх молекул. Ці сили для молекул, що знаходяться всередині рідини, взаємно скомпенсовані (рис.3.3.7). Рівнодійна ж сил притягання, що діє на молекули, які знаходяться на поверхні розділу, напрямлена вниз (всередину рідини), тобто молекули поверхні мають так звану надлишкову поверхневу енергію. На поверхні утворюється дефіцит молекул, через що відстань між молекулами набагато більша від норми, тому поверхневий шар рідини розтягнутий і між молекулами на поверхні діють сили притягання або сили поверхневого натягу. Мінімальну поверхню серед тіл певного об'єму має куля. Тому за відсутності (або дуже малої) дії сил рідина набуває форми кулі.

Підтвердженням цього є дослід Плато з руху краплини аніліну в посудині з рідиною, густина якої дорівнює густині аніліну.

Коефіцієнт поверхневого натягу дорівнює відношенню сили поверхневого натягу F_пов до довжини лінії l, що обмежує поверхню розділу і вздовж якої вона діє по дотичній в кожній точці, перпендикулярно до будь-якого елемента лінії розділу середовищ:

У СІ [s] = Н/м.

сили поверхневого натягу виконують роботу, що дорівнює за модулем і протилежна за знаком зміні енергії поверхневого шару DE:

A = - DE = - sDS, де DS - зміна площі поверхневого шару рідини; s - коефіцієнт поверхневого натягу. З рівності знаходимо:

Отже, коефіцієнт поверхневого натягу рідини чисельно дорівнює роботі ізотермічного утворення одиниці поверхні рідини за її незмінного об'єму. За цих умов у СІ [s] = Дж/м2

Поверхне́вий на́тяг — фізичне явище, суть якого в прагненні рідини скоротити площу своєї поверхні при незмінному об'ємі. Характеризується коефіцієнтом поверхневого натягу.

Завдяки силам поверхневого натягу краплі рідини приймають максимально близьку до сферичної форми, виникає капілярний ефект, деякі комахи можуть ходити по воді.

Поверхневий натяг виникає як у випадку поверхні розділу між рідиною й газом, так і у випадку поверхні розділу двох різних рідин.

Своєю появою сили поверхневого натягу завдячують поверхневій енергії.

№94 Змочування. Поверхнево-активні речовини. Абсорбція.

Поверхне́во-акти́вні речови́ни (ПАР, сурфактанти, детергенти) — хімічні речовини, які знижують поверхневий натяг рідини, полегшуючи розтікання і знижуючи поверхневий натяг на межі двох рідин. Це речовини, молекули або йони яких концентруються під дією молекулярних сил (адсорбуються) біля поверхні розділу фаз і знижують енергію поверхневу. У вужчому значенні ПАР здебільшого називають речовини, що знижують поверхневий натяг на межі поділу: рідина (вода) — повітря (пара), рідина (вода) — рідина (масло), рідина — тверда поверхня.Поверхнево-активні речовини — зазвичай амфіфільні органічні сполуки (термін амфіфільні означає, що вони містять як гідрофільні групи («хвости»), так і гідрофобні групи («головки»). Через таку будову вони розчинюються як у неполярних жирах і органічних розчинниках, так і в полярних середовищах (воді). Поверхнево-неактивні речовини – підвищують поверхневий натяг речовини.

Я кщо сили притягання між молекулами рідини і твердого тіла переважають сили притягання між молекулами рідини – змочування.

Абсорбція — вибіркове поглинання речовини з газового чи рідкого середовища усім об'ємом твердого тіла чи рідини. Наприклад рідини — твердою речовиною (чорнила — промокальним папером) чи газу — рідиною (аміаку — водою).

Абсорбція зумовлена ван-дер-ваальсовими, або електростатичними, силами притягання частинок адсорбованої речовини до частинок адсорбенту.

Оборотність процесу фізичної абсорбції створює сприятливі умови для послідовного проведення процесів абсорбції (поглинання речовини абсорбентом) та десорбції (вилучення з абсорбенту поглиненої речовини). Абсорбція широко застосовується в абсорбційній техніці, лежить в основі очищення, розділення газів та рідин тощо.

№95 Рідкі кристали. Полімери.

Рідки́й криста́л — специфічний стан термодинамічної системи, якому властиві риси як рідини (текучість), так і кристалу (анізотропія властивостей).

Рідкий кристал - проміжна фаза (мезофаза) між ізотропною рідиною і кристалічним твердим тілом. Рідкі кристали це флюїди, молекули яких певним чином впорядковані, тобто існує певна симетрія. Як наслідок, існує анізотропія механічних, електричних, магнітних та оптичних властивостей речовин цього класу. Поєднуючи властивості рідин та твердих тіл (текучість, анізотропія), рідкі кристали проявляють специфічні ефекти, багато з яких не спостерігаються у рідинах та твердих тілах. Зокрема, в рідких кристалах спостерігається подвійне променезаломлення,флексоелектричний ефект, перехід Фредерікса

Полімер — природніташтучні сполуки, молекулиякихскладаютьсязвеликогочислаповторюваниходнаковихаборізнихзабудовоюатомнихугруповань, з'єднанихміжсобоюхімічнимиабокоординаційнимизв'язкамивдовгілінійніаборозгалужені ланцюги. Структурніодиниці, зякихскладаютьсяполімериназиваютьсямономерами.

Розмір молекули полімеру визначається ступенем полімеризації n, тобто числом ланок у ланцюзі. Якщо n = 10…20, речовина відноситься до легких масел. Зі зростанням nзбільшується в'язкість, речовина стає воскоподібною, нарешті, при n = 1000 утворюється твердий полімер. Ступінь полімеризації необмежений: він може бути 10⁴, і тоді довжина молекул досягає мікрометрів. Молекулярна маса полімеру дорівнює добутку молекулярної маси мономера та ступеня полімеризації. Зазвичай молекулярна маса перебуває в межах 10³ … 3*10⁵. Більша довжина молекул перешкоджає їхньому правильному впакуванню, і структура полімерів варіює від аморфної до частково кристалічної. Частка кристалічності значною мірою визначається геометрією ланцюгів. Чим ближче укладаються ланцюги, тим більш кристалічним полімер стає. Кристалічність, зазвичай, навіть у найкращому разі виявляється недосконала.

Аморфні полімери плавляться в діапазоні температур, яка залежить не тільки від їхньої природи, але й від довжини ланцюгів; кристалічні мають точку плавлення.

В основу класифікації полімерів закладені різні ознаки: походження, склад, методи утворення, структура, галузі використання. Так за походженням полімери поділяються на:

1. природні або натуральні, до яких відноситься велика група (білки, крохмаль, целюлоза, натуральний каучук, природний графіт та ін.).

2. синтетичні — утворені синтезом з низькомолекулярних речовин — мономерів (поліетилен з етилену, полістирол із стиролу). Це ведуча група, тому що синтез дозволяє цілеспрямовано регулювати склад і властивості.

3. штучні — утворюються з природних полімерів шляхом їхньої хімічної модифікації (наприклад, при взаємодії целюлози з азотною кислотою утворюється нітроцелюлоза).

Природні полімери утворюються в результаті життєдіяльності рослин і тварин й утримуються в деревині, вовні, шкірі. До природних полімерів відносять протеїн, целюлоза, крохмаль,шелак, лігнін, латекс.

Фізичні властивості

Полімери здебільшого аморфні речовини. Довгі ланцюжки та велика молекулярна маса не дозволяють полімерам переходити до рідкого стану (швидше наступає хімічний розпад). Проте при підвищенні температури з полімерами відбуваються зміни — вони розм'якають і стають дуже пластичними. Температура переходу від крихкого стану до пластичного називається температурою склування. Температура склування не є чітко визначеною температурою фазового переходу, а радше вказує на температурний діапазон, у якому відбуваються зміни. При низьких температурах полімери є досить крихкими матеріалами.

Здебільшого використовуються механічні властивості полімерів. При температурі вищій за температуру склування їх неважко пресувати в довільну форму, при застиганні вони зберігають форму й можуть слугувати для інкапсуляції та інших цілей. Проте спряжені полімери дедалі частіше використовуються як органічні напівпровідники.

№96 Поняття фази. Крива фазової рівноваги.

Частину гетерогенної системи, що обмежена поверхнею розділу і характеризується за відсутності зовнішніх силових полів у всіх своїх точках однаковими фізичними властивостями, називають фазою. Ці властивості, звичайно, не залежать від кількості речовини. Так, система лід — вода — параскладається з трьох фаз, число яких у цьому разі збігається з агрегатними станами речовини. Взагалі не можна ототожнювати агрегатні стани з фазами. Алмаз і графіт — це дві різні тверді фази тієї самої речовини — вуглецю. Є кілька різновидів льоду, тобто твердої води.трифазними і т. д. Для однокомпонентної системи фазовий перехід першого роду (зміна агрегатного стану) визначається зовнішніми умовами – однозначним зв’язком тиску та температури. Такі переходи можна розглянути на фазових діаграмах стану в координатах „р – Т”. Фазові діаграми є сукупністю кривих, кожна точка яких відповідає стану динамічного рівноважного співіснування двох фаз. Ці криві називаються лініями фазової рівноваги.

Фазовий перехід, що характеризується однаковістю енергій Гіббса, співіснуючих у рівновазі фаз, і стрибкоподібним зміненням ентропії та обєму при переході речовини із однієї фази в іншу, називається переходом першого роду. Фазові переходи першого роду супроводжуються виділенням або поглинанням теплоти, яка називається прихованою теплотою фазового перетворення ΔНф Прикладами фазових переходів першого роду є випарювання, конденсація, плавлення, кристалізація, сублімація, а також переходи твердих речовин із однієї кристалічної модифікації в іншу Крім фазових переходів першого роду, існують фазові переходи другого роду. Для них характерна не тільки однаковість енергій Гіббса, але й однаковість ентропій та обємів співіснуючих у рівновазі фаз, тобто відсутність теплового ефекту процесу та змінення обєму при температурі перетворення. Зате мають місце стрибки фізичних величин, що виражені похідними ентропій та об¢єму: теплоємність С = T(dS/dT)P та коефіцієнт термічного розширення β

Прикладами фазових переходів другого роду є перехід речовини у надпровідниковий стан, перехід парамагнетику у ферромагнетик, перехід рідкого гелію у надтекучий стан.

№97 Випаровування, сублімація, топлення, кристалізація.

Випаро́вування — процес переходу рідини в газоподібний стан, відбувається при будь-якій температурі (на відміну від кипіння, що відбувається при певній температурі).

Рідина, залишена в блюдці, повністю випарується, тому що в будь-який час у ній є молекули, досить швидкі (з достатньою кінетичною енергією), щоб перебороти міжмолекулярні сили притягання на поверхні рідини і покинути її. Температура рідини, що випаровується, повинна знижуватися, тому що молекули, що її покидають, забирають кінетичну енергію. Швидкість випаровування зростає зі зростанням температури.

Випаровування супроводжується оберненим процесом — конденсацією пари. Якщо пара над поверхнею рідини насичена, то між процесами встановлюється динамічна рівновага, при якій кількість молекул, що покидає рідину в одницю часу дорівнює кількості молекул, що повертаються в неї. Якщо пара над рідиною ненасичена, то випаровування продовжуватиметься доти, доки пара не стане насиченою, або до повного висихання рідини.

Випаровування супроводжується зниженням температури, оскільки з рідини вилітають молекули з енергією, яка перевищує середню. Кількісно калориметрія випаровування характеризується питомою теплотою випаровування.

Зростанню швидкості випаровування сприяє вітер. Він забирає молекули пари з-понад поверхні рідини, заважаючи встановленню динамічної рівноваги. Для швидкого випаровування рідини, і пов'язаного з ним висушування, використовують потоки теплого повітря. Прикладом може бути побутовий фен.

Швидкість випаровування визначається поверхневою щільністю потоку пари, проникаючої за одиницю часу в газову фазу з одиниці поверхні рідини. Найбільше значення поверхневої щільності потоку пари досягається у вакуумі. При наявності над рідиною відносно щільного газового середовища випаровування сповільнюється.

Субліма́ція (лат. sublimo) — перехід речовини із твердого стану в газоподібний, оминаючи рідку фазу. Оскільки при сублімації змінюється питомий обсяг речовини і поглинається енергія (теплота сублімації), то сублімація є фазовим переходом першого роду.

Як і у рідинах, у твердих тілах завжди присутня деяка кількість молекул, енергія яких достатня для подолання притягання до інших молекул, і які здатні відірватись від поверхні тіла і перейти в навколишній простір. Для твердих тіл цей процес називається сублімацією.

Для більшості твердих тіл процес сублімації при нормальних температурах є незначним, і тиск пари над поверхнею твердого тіла малий; цей тиск підвищується із підвищенням температури. Інтенсивно сублімують такі речовини, як нафталін і камфора, що відчувається по різкому властивому їм запаху. Особливо інтенсивно сублімація проходить у вакуумі, що використовується у виготовленні дзеркал. Відомий приклад сублімації — перетворення льоду в пару — мокра білизна висихає на морозі.

Пла́влення (топлення) — перехід тіла з твердого стану в рідкий. Зворотний процес — тверднення (кристалізація). Плавлення відбувається з поглинанням теплоти і є фазовим переходом першого роду.

При нормальному тиску, найбільшою температурою плавлення серед металів має вольфрам (3422 °C), а серед складних речовин — карбід гафнію HfC (3890 °C). Можна вважати, що найнижчу температуру плавлення має гелій: при нормальному тиску він залишається рідким при скільки завгодно низьких температурах.

Багато речовин при нормальному тиску не мають рідкої фази. При нагріванні шляхом сублімації вони відразу переходять у газуватий стан.

Кристаліза́ція (рос. кристаллизация, англ. crystallisation, нім. Kristallisation, англ. Crystallization) — процес виділення з розчинунадлишку розчиненої речовини у вигляді кристалів або перехід речовини з газоподібного, рідкого (розчину чи розплаву) або твердого (аморфного) станів у кристалічний.

Кристалізація — процес утворення кристалів з пари, розчинів або розплавів та з речовини в іншому кристалічному або аморфному стані. Кристалізація починається при досягненні деяких граничних умов, наприклад, переохолодженні рідини або перенасиченні пари, коли практично миттєво виникає багато дрібних кристаликів — центрів кристалізації. Кристалики ростуть, приєднуючи атоми з рідини або пари. Ріст граней кристалу відбувається пошарово, краї незавершених атомних шарів (сходинки) при рості рухаються вздовж граней. Залежність швидкості росту від умов кристалізації приводить до різноманітності форм росту та структури кристалів (багатогранні, пластинчасті, голчасті, скелетні,дендритні та ін. форми, олівцеві структури і т. д.). В процесі кристалізації також виникають різні дефекти кристалічної ґратки (див. дислокації).

Якщо насичений привисокій температурі розчин твердої речовини охолодити, то з нього буде виділятися надлишок розчиненої речовини у вигляді кристалів, а в розчині залишатиметься така її кількість, яка утворює насичений розчин при нижчій температури, такий процес називається кристалізацією.

Процес кристалізації відбувається і при випарюванні розчину. При цьому внаслідок виділення певної кількості води ненасичений спочатку вихідний розчин стає насиченим, а потім і пересиченим, який легко розкладається, і надлишок розчиненої речовини виділяється у вигляді кристалів.

№98 Відносна вологість.

Вмістводяної пари у повітрі нечасто буваємаксимальним. Тому для визначення того, на скількиповітрянасиченевологоювпорівнянні з найбільшможливоїкількістю, існуєпоняттявідносноївологостіповітря. Вонопоказуєвідношення фактичного вмістуводяної пари у повітрі до максимально можливого при данійтемпературі й виражається у відсотках. По радіопід час прогнозу погоди нас повідомляютьсаме про відноснувологістьповітря. Насиченим водою є повітря з відносноювологістю 100%. В ньому вода починаєконденсуватися, тобтопереходити у газоподібного у рідкий стан. Так виникає роса або туман. Якщовідноснавологість не досягаєзазначеноїпозначки, повітрявважаєтьсяненасиченим. Відноснавологістьповітряпоблизуземноїповерхнізазвичайбільшазранку, коли щепрохолодно. Зпідвищеннямтемператури вдень відноснавологість, як правило, зменшується, навіть коли абсолютна кількість пари в нійзалишаєтьсянезмінною. Наприклад, якщозранку при температурі -5^ОС у повітрімістилося 3 г/м³ води, це означало, щовідноснавологість становить 100%, тобтоповітрябулонасиченимвологою. Коли вдень температура зросла до 0^ОС, а кількість води в повітрізалишиласянезмінною, відноснавологістьвжестановитимелише 60% й повітря стало ненасиченим водою. 

Як визначаютьвідноснувологістьповітря

Визначаютьвідноснувологістьповітряприладом, основною частиноюякого є знежиреналюдськаволосина.Йогоназиваютьволосянийгігрометр. Виявляється, людськеволоссяреагує на коливаннявідносноївологостіповітря, змінюючи свою довжину. При збільшеннівологостівоновитягується, при зменшенні – коротшає.Цізмінипередаються на стрілкуприладу й вона відхиляється