12.Устойчивость стержней при продольном изгибе. Формула Эйлера и условия ее применения. Гибкость стержней.

Соблюдение условий прочности и жесткости еще не гарантирует способности конструкций выполнять, предназначенные им функции в эксплуатационных режимах. Наряду с выполнением условий прочности и жесткости, необходимо обеспечить и устой­чивость конструкций.

При неизменной схеме нагружения, под устойчивостью пони­мается свойство способности системы сохранять свое первоначаль­ное равновесное состояние. Значения внешних сил, при которых происходит потеря устойчивости, называются кри­тическими.

Рассмотрим длинный тонкий стержень (рис. 30,а) нагруженный осевой сжимающей силой . В этом случае возможны две формы равновесия стержня: прямолинейная и криволинейная. При малых значениях силы стержень сжимается, оставаясь прямолинейным. Если его вывести из положения равновесия, то под действием упругих сил стержень, поколебавшись около положения равновесия, примет начальную форму. В этом случае устойчивой является прямолинейная форма (рис. 30,а).

Если увеличить сжимающую силу , то при некотором ее значении отклоненный от вертикального положения стержень не возвратится к первоначальному положению по устранению причины, отклонившей его. В этом случае устойчивой является криволинейная форма равновесия (рис. 30,б).

Значение силы, при которой первоначальная форма равновесия упругого тела становится неустойчивой, называется критической силой. Наименьшее значение сжимающей силы, при котором сжатый стержень теряет способность сохранять прямолинейную форму устойчивого равновесия, так же называют критической силой и обозначают .

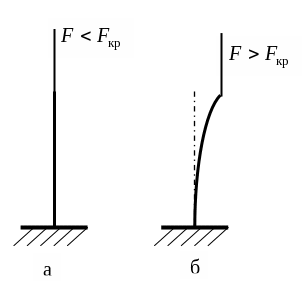
Рис. 30

Определение критической силы. Формула Эйлера. Рассмотрим решение задачи об устойчивости сжатого стержня силой , у которого оба конца закреплены шарнирно (рис. 31). Стержень искривился так, что в сечении прогиб составил .

Рис. 31

Записывая дифференциальное уравнение упругой линии балки, и ограничиваясь рассмотрением только малых перемещений, имеем: ,

где минимальный момент инерции сечения.

Изгибающий момент M_x (z), действующий в поперечном сечении стержня, расположенного на расстоянии z от начала системы координат, будет равен

При положительном прогибе в выбранной системе координат знак “минус” означает, что момент является отрицательным. Дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости в этом случае будет иметь вид: .

Обозначая , получим линейное дифференциальное уравнение второго порядка относительно прогиба

Общее решение данного уравнения имеет вид

где A и B – постоянные интегрирования.

Постоянные интегрирования определяем из условий равенства нулю прогибов стержня на опорах. В этом случае имеем: при z=0, y=0, A=0; z=l, y=0, Последнее соотношение справедливо при (n – любое целое число).

Откуда _, с учетом принятого ранее обозначения, получим

.

Минимальное действительное значение критической силы получится при n=1.

Это и есть формула Эйлера для определения критической силы.

Влияние способов закрепления концов стержня на критическую силу. Формула Эйлера получена для случая шарнирного закрепления концов стержня, когда потеря устойчивости происходит по одной полуволне. Для других случаев закрепления формула Эйлера принимает вид

где μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рис. 32).

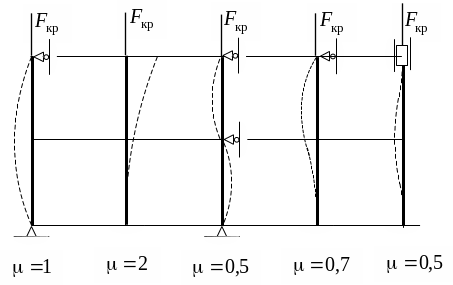
Рис. 32

Критические напряжения равны

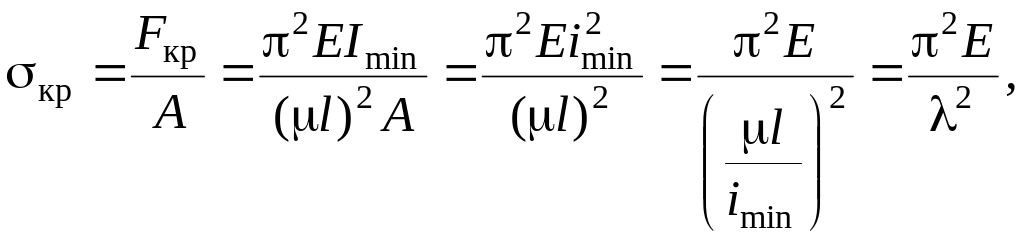
где минимальный радиус инерции;

гибкость стержня.

Пределы применимости формулы Эйлера. При выводе формулы для критических сил и напряжений, использовалось приближенное дифференциальное уравнение изогнутой оси балки, которое было получено в предположении, что материал стержня подчиняется закону Гука. Таким образом, формулу Эйлера можно применять только для значений напряжений, меньших или равных пределу пропорциональности

откуда . Таким образом, формула Эйлера может применяться при условии, что .

В случаях, когда гибкость стержня критическое напряжение определяется по эмпирическим зависимостям. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:

где постоянные величины, зависящие от материала стержня.