6) Работа и энергия, мощность. Кинетическая энергия. Консервативные и неконсервативные силы. Потенциальная энергия

Э нергия - универсальная мера различных форм движения и взаимодействия. Различные формы энергии связывают с различными формами движения материи: механическую, тепловую, электромагнитную, ядерную и пр. В одних случаях форма движения материи не изменяется (например, холодное тело нагревает горячее), в других - переходит в другую форму (например, механическое движение превращается в тепловое в результате трения). Однако существенно, что во всех перечисленных случаях энергия, отданная (в той или иной форме) от одного тела другому телу, равна энергии, которую получило последнее тело.  Изменение механического движения тела вызывается силами, которые действуют на него со стороны других тел. С целью количественно описать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.  Если тело движется прямолинейно и на него действует постоянная сила F, составляющая некоторый угол α с направлением перемещения, то работа этой силы равна проекции силы F_s на направление перемещения (F_s= Fcosα), умноженной на соответствующее перемещение точки приложения силы:  Но на практике сила может изменяться как по модулю, так и по направлению, поэтому формула (1) непригодна. Однако, если рассмотреть данную ситуацию для элементарного перемещения dr, то силу F мы считаем постоянной, а движение точки ее приложения - прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина  где α - угол между векторами F и dr; ds = |dr| - элементарный путь; F_s - проекция вектора F на вектор dr (рис. 1).  Если взять участок траектории от точки 1 до точки 2, то работа на нем равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Поэтому эту сумму можно привести к интегралу  Чтобы вычислить интеграл (2) надо знать зависимость силы F_s, от пути s вдоль траектории 1-2. Пусть эта зависимость представлена графически (рис. 2), тогда искомая работа А равна на графике площадью заштрихованной фигуры. Если точка движется прямолинейно, сила F=const и α=const, то получим  где s - пройденный телом путь (см. также формулу (1)).  Из формулы (1) следует, что при α<π/2 работа силы положительна, в этом случае составляющая F_s совпадает по направлению с вектором скорости точкиv (см. рис. 1). Если α>π/2, то работа силы отрицательна. При α= π/2 (сила и перемещение перпендикулярны) работа силы равна нулю.  Единица работы - джоуль (Дж): 1 Дж - работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н•м).  Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:  За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени  т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N - величина скалярная.  Единица мощности - ватт (Вт): 1 Вт - мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).

Кинети́ческаяэне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательногодвижения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленнаядвижением.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы  . Учитывая, что  , Получим:

Если система замкнута, то есть  , то  , а величина

о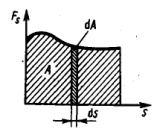 стаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:  — масса тела  — скорость центра масс тела  — момент инерции тела  — угловая скорость тела.

Все силы, встречающиеся в механике , принято разделять на консервативные и неконсервативные.

Сила, действующая на материальную точку, называется консервативной (потенциальной), если работа этой силы зависит только от начального и конечного положений точки. Р абота консервативной силы не зависит ни от вида траектории, ни от закона движения материальной точки по траектории (см. рис. 2):  .

Изменение направления движения точки вдоль малого участка на противоположное вызывает изменение знака элементарной работы  , следовательно,  . Поэтому работа консервативной силы вдоль замкнутой траектории 1a2b1 равна нулю: .

Точки 1и 2, а также участки замкнутой траектории 1a2 и 2b1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю:

 или  .В этой формуле кружок на знаке интеграла показывает, что интегрирование производится по замкнутой траектории. Часто замкнутую траекторию L называют замкнутым контуром L (рис. 3). Обычно задаются направлением обхода контура L по ходу часовой стрелки. Направление элементарного вектора перемещения  совпадает с направлением обхода контура L. В этом случае формула (5) утверждает: циркуляция вектора  по замкнутому контуру L равна нулю.

Следует отметить, что силы тяготения и упругости являются консервативными, а силы трения неконсервативными. В самом деле, поскольку сила трения направлена в сторону, противоположную перемещению или скорости, то работа сил трения по замкнутому пути всегда отрицательна и, следовательно, не равна нулю.

Потенциальная энергия   в поле тяготения Земли вблизи поверхности приближённо выражается формулой: , где   — масса тела,   — ускорение свободного падения,   — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

О физическом смысле понятия потенциальной энергии

• Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле.

• Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел.

• Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.