
- •1.Числовые ряды. Необходимый признак сходимости. Простейшие свойства числовых рядов. Сходимость ряда, составленного из членов бесконечной геометрической прогрессии
- •Если модуль q≠0
- •2. Признаки сходимости рядов с неотрицательными членами
- •3. Знакопеременные ряды. Абсолютные и условные сходимости. Признак Лейбница.
- •4. Функциональные ряды
- •5. Непрерывность суммы равномерно сходящегося функционального ряда. Почленное интегрирование и дифференцирование функциональных рядов.
- •6. Степенные ряды. Теорема Абеля. Радиус сходимости степенного ряда.
- •7. Ряды Тейлора и Маклорена
- •8. Разложение элементарных функций в ряды Тейлора
- •9. Определение, геометрический смысл, теорема о существовании двойного интеграла (ди)
- •10. Свойства двойного интеграла
- •11.Вычисление двойного интеграла
- •12.Замена переменных в двойном интеграле
- •13.Вычисление площадей и объемов с помощью двойных интегралов
- •14. Механические приложения двойного интеграла
- •15. Тройной интеграл. Вычисление тройного интеграла.
- •16.Замена переменных в тройном интеграле.
- •17.Криволинейные интегралы первого рода
- •18 Поверхностные интегралы 1 рода
- •20. Формула Грина
- •21. Независимость криволинейного интеграла от пути интегрирования.
- •22. Скалярные поля. Производная по направлению. Градиент.
- •23.Вычисление Поверхностных интегралов второго рода (пи-2)
- •24. Векторные поля
- •25.Циркуляция и ротор векторного поля. Теорема Стокса.
- •26. Определение графа. Ориентированные и неориентированные графы. Степени и кратности вершин. Число ребер неориентированного графа. Матрицы смежности и идентичности.
- •27. Определение Графа. Цель, маршрут. Эйлеровы графы
12.Замена переменных в двойном интеграле
Пусть на плоскости ХОУ задана область, ограниченная линией L. Предположим, что осуществляется замена переменных: x=x(u;v), y=(u;v) (*), причем функции x(u;v) и y(u;v) взаимно однозначны и дифференцируемы в области D.
Тогда формулы (*) устанавливают взаимооднозначное соответствие между точками (x;y) D и (u;v) D'.
Прямым y=const и v=const на плоскости ХОУ будут соответствовать некоторые кривые, поэтому координаты u и v называют криволинейными.
Разобьем
область D'
на прямоугольные площадки прямыми
y=const
и v=const,
тогда область D
с соответствующими кривыми разобьется
на четырехугольники: (•)ка P1(x(u;v);
y
(u;v));
P2
(x(u;v+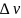 );
y(u;v+
));
P3
(x(u+
);
y(u;v+
));
P3
(x(u+ ;v+
);
y(u+
;v+
));
P4
(x(u+
;v);
y(u+
;v))
;v+
);
y(u+
;v+
));
P4
(x(u+
;v);
y(u+
;v))
Заменим приращение
функции их дифференциалами, пренебрегая
бесконечно малыми величинами. Тогда
P1(x(u;v);
y
(u;v));
P2
(x(u;v)+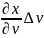 ;
y(u;v)+
;
y(u;v)+ );
);
P3
(x(u;v)+ ;
y(u;v)+
;
y(u;v)+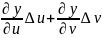 );
P4
(x(u;v)+
);
P4
(x(u;v)+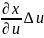 ;
y(u;v)+
;
y(u;v)+ )
)
Заметим,
что векторы
 (
( )
и
)
и
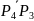 (
)
равны, значит наше допущение позволяет
считать прямоугольник P1P2
P3
P4
параллелограммом.
(
)
равны, значит наше допущение позволяет
считать прямоугольник P1P2
P3
P4
параллелограммом.
Найдем его площадь:
 =
=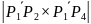
 =
= =
=
 =
=
Опр.1
Определитель
I= называется
Якобианом данных функций x(u;v)
и y
(u;v)
называется
Якобианом данных функций x(u;v)
и y
(u;v)
Т.о.
 Очевидно,
что если max размеры площадок стремятся
к 0,то lim
=
Очевидно,
что если max размеры площадок стремятся
к 0,то lim
=
Max
диаметры площадок, т.е. наибольшее
расстояние между точками
Поэтому


Т.о.

Двойной интеграл в полярных координатах
Напомним, что
полярные координаты задаются осью и
точкой на ней (полюсом). Положение любой
точки плоскости характеризуется двумя
координатами: расстоянием
от точки до полюса и углом наклона
радиус-вектора точки к полярной оси.
Если ось x выбрать совпадающей с полярной
осью, а ось у провести через полюс, то
формулы перехода от декартовых координат
к полярным следующие: x= cos
;
y=
sin
.
cos
;
y=
sin
.
I= =
= =
= =
=
Если область D правильная относительно полюса, т.е. любой луч, исходящий из полюса пересекает границу области не более чем в двух точках, то ее можно изобразить так:
B







M
N
AN – линия входа =1()M
M
BN – линия выхода =2()
A
2
1
O



13.Вычисление площадей и объемов с помощью двойных интегралов
В геометрии используются следующие свойства двойного интеграла:
 – площадь области
– площадь области
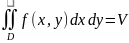 - объем цилиндрического
тела, ограниченного сверху поверхностью
z=
- объем цилиндрического
тела, ограниченного сверху поверхностью
z=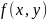 ,
снизу – областью D
и вертикальными образующими.
,
снизу – областью D
и вертикальными образующими.
14. Механические приложения двойного интеграла
В геометрии
используется след. св-ва дв. интеграла:
 ;
;

С точки зрения
механики
 -масса
пластинки D
с плотностью
-масса
пластинки D
с плотностью
 .
.
Опр.1 Статическим моментом материальной точки относительно оси наз. произведение массы точки на расстояние до оси:
если
точка М(х;у) имеет массу m,
то
 =my;
=my;
 =mx.
=mx.
Опр.
2 Стат.
моментами
и
системы мат. точек относит. осей Ох и Оу
наз. выражение
 ;
;
 .
.
Для определения
стат. моментов плоской области D
ее разбивают произвольным образом на
элементарные площадки
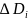 ,
каждую из которых считают однородной
с плотностью
,
каждую из которых считают однородной
с плотностью
 ,
где
,
где
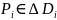 .
Затем элементарную фигуру
.
Затем элементарную фигуру

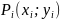 с массой
с массой
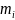 =
= .
Тогда
.
Тогда
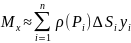 ,
а
,
а
 .
Переходя к пределу при
.
Переходя к пределу при
 получим
получим
 ;
;
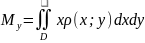 .
.
В механике важную роль играет понятие центра тяжести (центра масс)-точки, в которой «сосредоточена» вся масса тела.
Опр.
3 Центром
масс плоской фигуры D
называется такая точка C( ),
что
=М
),
что
=М ;
;
 =М
=М .
.
Из опр.3 следует,
что ;
;
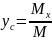 .
Т.о.
.
Т.о.
 ;
;
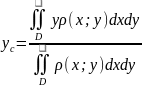 .
Если однородная фигура имеет ось
симметрии, то центр масс лежит на этой
оси.
.
Если однородная фигура имеет ось
симметрии, то центр масс лежит на этой
оси.
Моменты инерции
определяются аналогично стат. моментам,
только вместо расстояния до оси фигурирует
квадрат этого расстояния. Поэтому для
плоской пластинки D
с плотностью
моменты инерции находятся по формулам:
 =
= ;
;
 =
= ;
;
 =
= - момент инерции относительно начала
координат.
- момент инерции относительно начала
координат.
