2. Дифференциал функции. Приращение переменной в точке называют также дифференциалом в точке и обозначают Таким образом,

Определение. Пусть функция дифференцируема в точке . Дифференциалом в точке называют выражение

Замечание. Из данного определения и соответствующих свойств производной вытекают следующие свойства дифференциала функции:

1)

2) , где const.

3) , где const.

3. Геометрический и физический смысл производной.

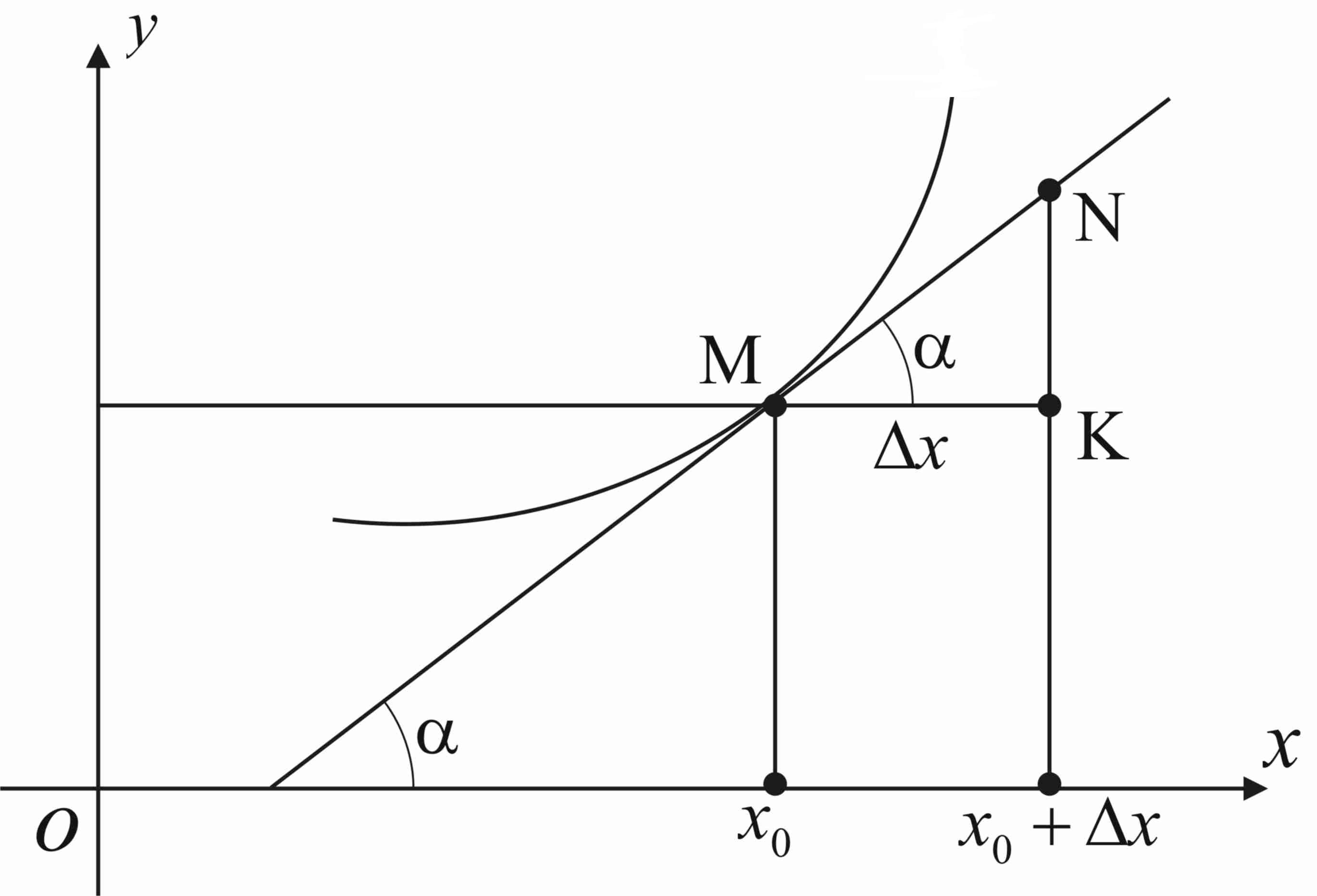Производная функции в точке равна , где - угол наклона касательной к графику функции в точке . (См. рис.).

Следовательно, уравнение касательной к графику функции в точке имеет вид: , где .

Из рисунка виден также и геометрический смысл дифференциала: tg

Таким образом, дифференциал функции в точке равен приращению ординаты вдоль касательной, проведенной к графику функции в точке .

Физический смысл производной:

Пусть - путь, пройденный материальной точкой, движущейся прямолинейно, в момент времени . Тогда - есть мгновенная скорость точки в момент времени .

4. Исследование функций на монотонность и экстремумы.

Производная помогает также при исследовании функции на возрастание и убывание. Напомним вначале соответствующее определение.

Определение . Пусть функция определена на промежутке . Говорят, что она возрастает ( убывает) на промежутке , если таких, что .

Теорема. Если функция дифференцируема на интервале и , то возрастает (убывает) на интервале .

Пусть производная функции непрерывна на промежутке . Для исследования ее на возрастание и убывание обычно придерживаются следующего плана:

1) Найти точки, где . Эти точки называются стационарными.

2) Во всех промежутках, на которые разбивают стационарные точки, определить знак . Для этого достаточно определить знак в одной точке каждого промежутка (знак внутри каждого промежутка не меняется, поскольку в противном случае внутри этого промежутка по теореме Больцано-Коши должен быть нуль производной, что невозможно). Если внутри промежутка , то здесь согласно теореме возрастает. Если , то убывает.

Пример. Исследовать на возрастание и убывание функцию

.

Данная функция дифференцируема на всей числовой прямой.

1) . Найдем критические точки : .Дискриминант ; ; ; .

2) Точки , разбивают числовую прямую на три интервала: , , .

+ - + На первом интервале возьмем .

-2 1 ;

Следовательно, на промежутке возрастает. На промежутке возьмем . . Поэтому убывает. На интервале возьмем . . Поэтому на интервале возрастает.

Определение. Пусть функция определена в . Точка называется точкой локального максимума (минимума),если такая, что

(1)

Если неравенства (1) строгие при , то точка называется точкой строгого локального максимума (минимума). Точки локального максимума и минимума называются точками экстремума.

Теорема. (необходимое условие экстремума). Если функция дифференцируема в точке и является точкой экстремума, то

Замечание. Из теоремы следует, что точки экстремума функции нужно искать среди критических точек и точек, где производная не существует. Одно из достаточных условий экстремума непосредственно вытекает из следующей теоремы .

Теорема (достаточное условие экстремума). Пусть функция непрерывна в точке и дифференцируема в . Тогда:

а) если производная при переходе через точку меняет знак с плюса на минус, то точка является точкой локального максимума;

б) если производная при переходе через точку меняет знак с минуса на плюс, то точка является точкой локального минимума функции .

Заметим, что из теоремы следует, что в примере 2 точка является точкой локального максимума, а точка является точкой локального минимума функции .

Часто при решении различных задач приходится находить наибольшее и наименьшее значения функции на некотором множестве .

Рассмотрим как решается эта задача сначала для случая, когда это отрезок . Пусть функция непрерывна на отрезке и дифферецируема на интервале за исключением, быть может, конечного числа точек

Тогда, согласно теореме Вейерштрасса функция достигает на отрезке наибольшее и наименьшее значения.

Из приведенных теорем следует следующий план отыскания наибольшего и наименьшего значений функции непрерывной на отрезке .

Найти производную и критические точки на интервале .

Найти значения

а) в критических точках;

б) на концах отрезка ;

в) в точках, где производная не существует.

Из полученных чисел выбрать наибольшее и наименьшее.

Замечание 1. Заметим, что находить промежутки возрастания и убывания здесь совсем не обязательно.

Замечание 2. Если является интервалом, полуинтервалом или бесконечным промежутком, то выше приведенным планом пользоваться нельзя. В этом случае для решения задачи о наибольшем и наименьшем значении нужно найти промежутки возрастания и убывания функции, пределы в граничных точках области определения и с помощью не сложного анализа получить ответ.

Пример 3. Найти наибольшее и наименьшее значения функции на промежутке .

Найдем промежутки возрастания и убывания. Для этого найдем производную:

Далее действуем по плану. Найдем нули производной:

Точка разбила промежуток на два интервала: и . Найдем на них знак производной. Для этого вычислим

Таким образом на интервале функция убывает, а на промежутке возрастает. Поэтому Наибольшего значения не существует, так как . В этом случае пишут: .