20. Непрерывность функции.
Определение.
Пусть функция
определена
на промежутке
,
.
Функция
называется непрерывной в точке
,
если предел функции и ее значение в этой
точке равны, т.е.
Пример.
Доказать
непрерывность функции
в точке
.
таким
образом
данная
функция непрерывна в точке
.
Замечание.
Если
(
),
то функция
называется непрерывной в точке
справа
(слева). Если функция
непрерывна
в точке
справа и слева, то она непрерывна в этой
точке.
Рассмотрим
другое определение непрерывности
функции в точке. В равенстве
перенесем
в левую часть и внесем
под знак предела. Так как при
,
то получим
Разность
называется приращением аргумента
в точке
,
и обозначается
Разность
называется приращением функции в точке
.
Таким образом
,
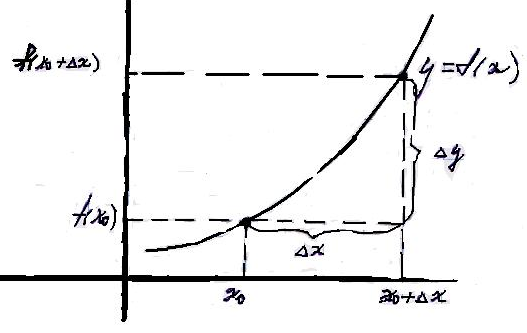
Тогда
равенство
примет вид
.
Определение.
Функция
называется непрерывной в точке
,
если ее приращение в этой точке является
бесконечно малой функцией при
.
Теорема.
Пусть
функции
и
непрерывны в точке
.
Тогда функции
,
и
также
непрерывны в точке
(
при
).
Замечание.
Простейшим
примером функции, непрерывной в любой
точке
числовой прямой, служит постоянная
функция
.
Другими
примерами непрерывных функций служат
Дробно-рациональная функция непрерывна во всех точках, в которых ее знаменатель отличен от 0.
Вообще, любая элементарная функция непрерывна в любой точке своей области определения.
21. Продолжение вычисления пределов функции.
Пример.
А)
Б)
В)
,
т.к.
Замечание.
При
вычислении пределов функций при
,
,
,
содержащих радикалы, надо рассматривать
арифметическое значение корня
при
и
.
Пример.
А)
.
При
имеем
.
Тогда
.
Б)
.
При
имеем
.
Тогда
.
В)
не существует, т.к. приделы этой функции
при
и
разные.
Замечание.
Говорят, что сумма двух бесконечно
больших функций разных знаков есть
неопределенность вида
П
ример.
а)
б)
,
т.к сумма двух положительных бесконечно
больших функций есть бесконечно большая
функция.
Говорят, что произведение бесконечно малой функции на бесконечно большую есть неопределенность вида 0*
Пример
Сделаем
замену переменной
.Тогда
=
=
Производная функции.
1. Определение и свойства.
К понятию производной приводит задача о вычислении мгновенной скорости движущейся материальной точки, задача о вычислении скорости изменения стоимости акций, задача о касательной к кривой и другие задачи.
Определение.
Пусть функция
определена в некоторой окрестности
точки
.
Производной функции называется
(1)
Если
предел в (1) существует, то функция
называется дифференцируемой в точке
.
В противном случае говорят, что функция
не имеет производной в точке
или не дифференцируема точке
.
Для обозначения производной используются также символы:
Обозначим
и
называются приращениями аргумента и
функции соответственно. Тогда
и
при
.
Поэтому равенство (1) можно переписать
так :
.
Определение.
Функция
называется дифференцируемой на промежутке
R,
если она дифференцируема в каждой точке
этого промежутка.
Сформулируем основные правила дифференцирования.
Пусть
и
дифференцируемые в точке
функции и
const.
Тогда
(производная
константы равна 0);
;
Правило
дифференцирования сложной функции.
Пусть
функция
дифференцируема в точке
,
а функция
дифференцируема в точке
.Тогда
сложная функция
дифференцируема в точке
и
Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Приведем таблицу производных основных элементарных функций.
8.
tg
9.
ctg
12.
arctg
13.
arcctg
Формулы
1. – 9. данной таблицы получаются из
таблицы пределов с помощью правил
Например,
Здесь мы использовали формулу (2) и
правило 4.
Используя правила дифференцирования 1.- 6. и таблицу производных можно найти производную любой элементарной функции.
Пример 1.
Пример
2. Пусть
.
Найти
.
Выделим у этой сложной функции внешнюю
и внутреннюю функции:
,
где
Пользуясь правилом 6, найдем
.
Замечание 1. Из предыдущего примера видно, как важно при вычислении производной сложной функции правильно выделить внешнюю и внутреннюю функции.
Замечание
2. Если
функция
дифференцируема
в точке
,
то
непрерывна в точке
.
Действительно,
Обратное
неверно.
То
есть дифференцируемая в точке
функция может не иметь производной в
точке
.
Например, функция
непрерывна
при всех
,
но не дифференцируема при
Задача. Доказать, что функция не дифференцируема при