
- •Вопрос 31. Логические связки;
- •Вопрос 32.Конъюнкция высказывания
- •Вопрос 33. Дизъюнкция высказываний
- •Вопрос 34.Конъюнкция предикатов (учебник стр. 62-63)
- •Вопрос 35. Дизъюнкция предикатов. Квантор общности. (учебник стр 63-64)
- •Вопрос 36. Квантор общности
- •Вопрос 37. Квантор существования
- •Вопрос 38 и 39. Отрицание высказываний и предикатов(высказываний и высказывательных форм)
- •Вопрос 40. Законы де Моргана
Вопрос 34.Конъюнкция предикатов (учебник стр. 62-63)
Предика́т — это то, что утверждается о субъекте. Субъектом высказывания называется то, о чём делается утверждение.
Далее в этой статье слово предикат используется в значении высказывательной формы
Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х , обозначают А(х) В(х).
Если Т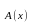 -
множество истинности высказывательной
формы А(х), а Т
-
множество истинности высказывательной
формы А(х), а Т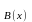 -
множество истинности высказывательной
формы В(х), то Т
-
множество истинности высказывательной
формы В(х), то Т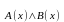 = Т
Т
.
= Т
Т
.
Пример: На множестве Х={1,2,3,4,5,6,7,8.} заданы высказывательные формы А(х)- х 6, и В(х)- х – четное число. Найти Т .
Решение: найдем Т и Т .
Т ={1,2,3,4,5.}
Т ={2,4,6,8.}
А(х) В(х) – х число четное и меньше шести.
Т = Т Т = {2,4.}
Вопрос 35. Дизъюнкция предикатов. Квантор общности. (учебник стр 63-64)
Дизъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х , обозначают А(х) В(х).
Если Т
-
множество истинности высказывательной
формы А(х), а Т
-
множество истинности высказывательной
формы В(х), то Т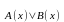 = Т
Т
.
= Т
Т
.
Пример: На множестве Х={1,2,3,4,5,6,7,8.} заданы высказывательные формы А(х)- х 6, и В(х)- х – четное число. Найти Т .
Решение: найдем Т и Т .
Т ={1,2,3,4,5.}
Т ={2,4,6,8.}
А(х) В(х) – х число четное или меньше шести.
Т = Т Т = {1,2,3,4,5,6,8.}
Квантор общности. Выражение «для всякого х»в логике называется квантором общности по переменной х (переменная может быть обозначена и другой буквой ) и обозначается символом х
Запись (х) [A(х)] означает: «для всякого значения х предложение A(х) – истинное высказывание» Иногда эту запись дополняют обозначение множества Х , на котором задана высказывательная форма A(х), и тогда предложение (хХ) [A(х)] можно читать;
А) для всякого х множество Х истинно A(х)
Б)всякой элемент из множества Х обладает свойством А
Вопрос 36. Квантор общности
Операцией связывания
квантором общности называется
правило, по которому каждому одноместному
предикату ![]() ,
определенному на множестве
,
определенному на множестве ![]() ,
сопоставляется высказывание,
обозначаемое
,
сопоставляется высказывание,
обозначаемое ![]() (читается:
"для всякого [значения]
(читается:
"для всякого [значения] ![]() [истинное
высказывание]"), которое истинно в
том и только в том случае, когда
предикат
тождественно
истинен, и ложно в противном случае,
[истинное
высказывание]"), которое истинно в
том и только в том случае, когда
предикат
тождественно
истинен, и ложно в противном случае,
При
чтении высказывания
слова
в квадратных скобках могут опускаться.
Высказывание
называется универсальным
высказыванием для
предиката
.
Символ ![]() происходит
от первой буквы англ. all —
"все". Сам символ
происходит
от первой буквы англ. all —
"все". Сам символ ![]() также
называют квантором общности по
переменной
также
называют квантором общности по
переменной ![]() .
.
Например,
рассмотрим два одноместных предиката
на множестве ![]() "
"![]() "
и "
"
и "![]() ".
Первый предикат тождественно истинный,
поэтому применение к нему операции
связывания квантором общности дает
истинное высказывание:
".
Первый предикат тождественно истинный,
поэтому применение к нему операции
связывания квантором общности дает
истинное высказывание: ![]() —
"для всякого
число
1 не превосходит
".
Второй предикат опровержим, поэтому
операция связывания квантором общности,
примененная к нему, дает ложное
высказывание:
—
"для всякого
число
1 не превосходит
".
Второй предикат опровержим, поэтому
операция связывания квантором общности,
примененная к нему, дает ложное
высказывание: ![]() —
"для любого
число
является
делителем числа 30".
—
"для любого
число
является
делителем числа 30".
В выражении переменная уже перестает быть переменной в обычном смысле этого слова, т. е. вместо нее невозможно подставлять какие бы то ни было конкретные значения. Считают, что переменная связанная, кажущаяся или немая. Такая ситуация уже встречалась в математике: переменные могут быть связаны не только квантором. Так, связанными являются переменные в следующих выражениях:
Это
означает, что каждое из приведенных
выражений не зависит от связанных
переменных, т. е. сущность выражения не
изменится, если связанную переменную
обозначить любой другой буквой. Так,
первое из трех выражений вне зависимости
от переменной равно 2, второе равно 0, а
третье — действительная полупрямая ![]() .
Аналогично, высказывание
может
быть прочитано так: "1 не превосходит
всякое натуральное число" — и в таком
виде оно вообще не содержит переменных.
.
Аналогично, высказывание
может
быть прочитано так: "1 не превосходит
всякое натуральное число" — и в таком
виде оно вообще не содержит переменных.
Если
одноместный предикат
задан
на конечном множестве ![]() ,
то нетрудно понять, что высказывание
эквивалентно
(имеет то же логическое значение)
конъюнкции
,
то нетрудно понять, что высказывание
эквивалентно
(имеет то же логическое значение)
конъюнкции ![]() .
В самом деле, по определению 20.1 истинность
высказывания
означает,
что предикат тождественно истинен, т.е.
каждое из высказываний
.
В самом деле, по определению 20.1 истинность
высказывания
означает,
что предикат тождественно истинен, т.е.
каждое из высказываний ![]() ,
в которые этот предикат превращается,
истинно. Последнее равносильно истинности
конъюнкции
.
,
в которые этот предикат превращается,
истинно. Последнее равносильно истинности
конъюнкции
.
Следовательно, для предикатов, заданных на конечном множестве, операция связывания квантором общности может быть выражена через конъюнкцию. Для предикатов, заданных на бесконечном множестве, такого сделать нельзя, и в этом случае операция связывания квантором общности является существенно новой.
Можно подметить еще одну особенность операции связывания квантором общности по сравнению с операциями из предыдущей лекции. Те операции ставили в соответствие одному или двум предикатам новый предикат, а операция связывания квантором общности сопоставляет предикату высказывание. На это можно сказать следующее. Во-первых, каждое высказывание для достижения большей общности сейчас и в дальнейшем можно рассматривать как предикат, содержащий 0 предметных переменных, т. е. как нульместный предикат. Во-вторых, мы пока применяли квантор общности лишь к одноместным предикатам. Переходим к рассмотрению вопроса о применении операции связывания квантором общности к предикатам с любым числом предметных переменных; такая операция предстанет операцией в полном смысле слова: предикатам она будет сопоставлять предикаты.
