СжДм-113 Математика, экзамен, I семестр.

1. Определители. Элементарные преобразования и свойства определителей.

Определитель – число, записанное в виде квадратных чисел. Определитель характеризует содержание матрицы (аля Википедия).

Свойства: 1) Равноправность строк и столбцов

2) При перестановке двух параллельных рядов определитель меняет знак

3) Определитель, имеющий два одинаковых ряда равен 0

4) Общий множитель элементов какого-либо ряда определителя можно вывести за знак определителя

5) Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух определителей

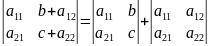
6) (Элементарные преобразования определителей) Если к элементам одного ряда прибавить соответствующие элементы другого ряда, умноженные на любое число

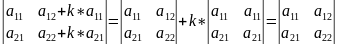
7) Определитель, у которого строки и столбцы соответственно пропорциональны равен 0

2. Вычисление определителей 2 и 3 порядка. Вычисление определителей разложением по элементам строки (столбца).

Определитель второго порядка равен разности произведений главной диагонали и побочной диагонали.

Определитель третьего порядка вычисляется по правилу треугольника и с помощью алгебраических дополнений.

Минор – определитель 1-го порядка, полученный путем из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.

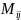
Алгебраическое дополнение некоторого элемента 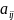– минор, взятый со знаком «+» (если i+g= четное число) или «-» (если i+g= нечетное число).

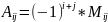
Определитель равен сумме произведений элементов некоторого столбца (строки) на их алгебраические дополнения. Пример:

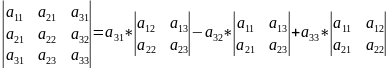
3. Матрицы. Действия над матрицами. Обратная матрица.

Матрица – прямоугольная таблица чисел, содержащая n строк и m столбцов одинаковой длины.

Матрица, у которой количество столбцов равно количеству строк, называется квадратной.

Квадратная матрица, у которой все элементы, кроме главной диагонали, равны 0, называется диагональной.

Диагональная матрица, у которой элементы главной диагонали равны 1, называется единичной (Е).

Квадратная матрица, у которой одни элементы, расположенные по одну сторону от главной диагонали, равны 0, называется треугольной.

Матрица, у которой n или m равен 1 называется вектором.

Матрица, у которой n=m=1 называется скаляром.

Матрицы эквивалентны, если одна получается из другой путем элементарных преобразований. Элементарные преобразования матрицы:

1. Перестановка местами двух столбцов или строк

2. Умножение всех элементов строки или столбца на число

3. Прибавление одной строки (столбца) к другой строке(столбцу), при необходимости умножив

Действия над матрицами:

1. Равенство: А=В, когда

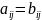
2. Сложение: А+В, когда 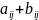А+(В+С)=(А+В)+С А+0=А

3. Умножение на число: k*A, когда 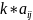;  (λβ)A = λ(βA), (λ+β)A = λA + βA, λ(A+B) = λA + λB

4. Транспонирование

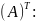
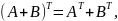
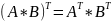
5. Умножение на матрицу (А*В): 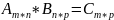. Количество столбцов в матрице A должно совпадать с количеством строк в матрице В. Свойства умножения матриц:

1. Ассоциативность (AB)C = A(BC), (λA)B = λ(AB)

2. Некоммутативность АВ≠ВА

Если определитель матрицы равен 0, то матрица вырождена, иначе – не вырождена. Всякая невырожденная матрица имеет обратную матрицу. Матрица называется обратной, если выполняется условие А*А^-1= А^-1*А=Е. Всякая невырожденная матрица имеет обратную.

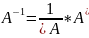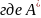, - матрица алгебраических дополнений, подвергнутая транспонированию.