В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.

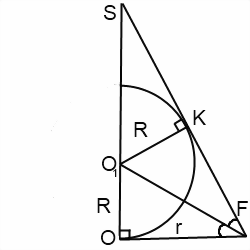
И так, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.

Прямоугольные треугольники OO1F и KO1F равны (по катетам и  гипотенузе). Отсюда KF=OF=r.

Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что

    В треугольнике SOF применим свойство биссектрисы

    И з прямоугольного треугольника OO1F

    При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.

   

   

    Теперь найдем отношение объема пирамиды к площади ее поверхности:

   

    Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:

   

Решить задачу.

Д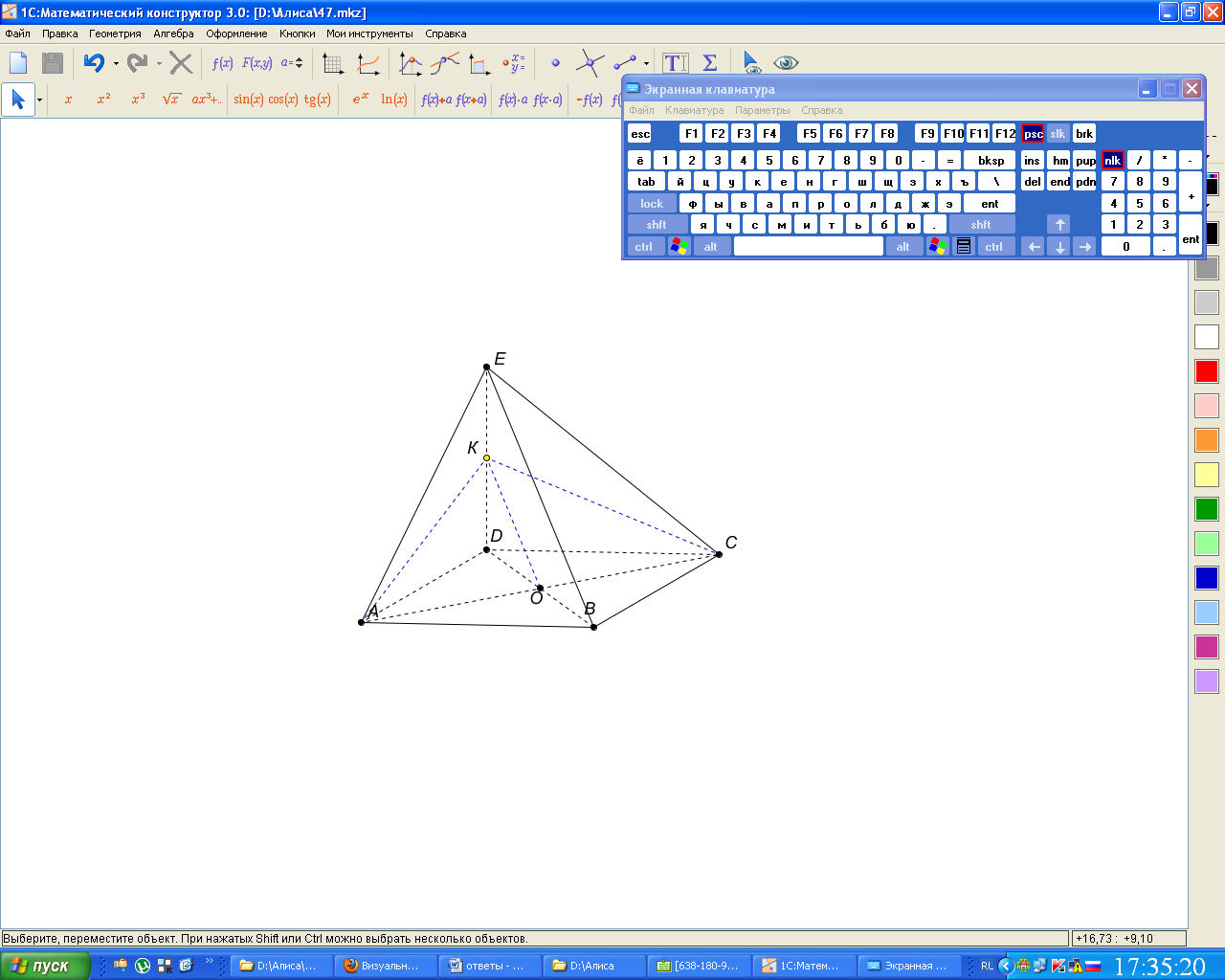 ано: ЕАВСД – пирамида (АВ=ВС=СД=АД=4, ), (ЕАД) (АВСД), (ЕДС) (АВСД),

ВД=АС=ЕД.

Найти:

Решение:

I. построение:

1)

2)

3) (ОК)

II. Доказать, что

1) (АЕД) (АВСД) (по усл), (ЕДС) (АВСД) (по усл)

ЕД (АВСД) (по теореме о двух пересекающихся плоскостях, перпендикулярных третьей плоскости)

ЕД – высота ЕАВСД

2) О=АС ДВ (по построениею)

ДО=ОВ (т.к. АВСД – квадрат)

ДК=КЕ (по построению)

ОК- средняя линия ЕДВ (по определению средней линии треугольника)

ОК ЕВ (по теореме о средней линии треугольника)

ВЕ (АСК) (по теореме о параллельности прямой и плоскости)

III. Вычисления:

1) АС - ? АС –диагональ АВСД

2) КО-? Рассм : КД = ДО =

3)

АК=КС (т.к. АКД= КДС (по двум сторонам и углу между ними))

КО-высота АКС

Ответ:

Теоретические основы решения:

1) теорема о двух пересекающихся плоскостях, перпендикулярных третьей плоскости

2) теорема о параллельности прямой и плоскости

3) определение средней линии треугольника

4) теорема о средней линии треугольника

5) определение квадрата

6) первый признак равенства треугольников

7) формула площади треугольника

8) теорема Пифагора

Затруднения возможны:

1) При построении сечения пирамиды

2) при построении пирамиды с двумя пересекающимися гранями, перпендикулярных основанию

3) при нахождении площади треугольник

58. Решить задачу на построение сечения многогранника.

Дано: ЕАВСД – пирамида, Р (ЕАВ), Т (ЕАД), М (ЕСД).

Построить : |

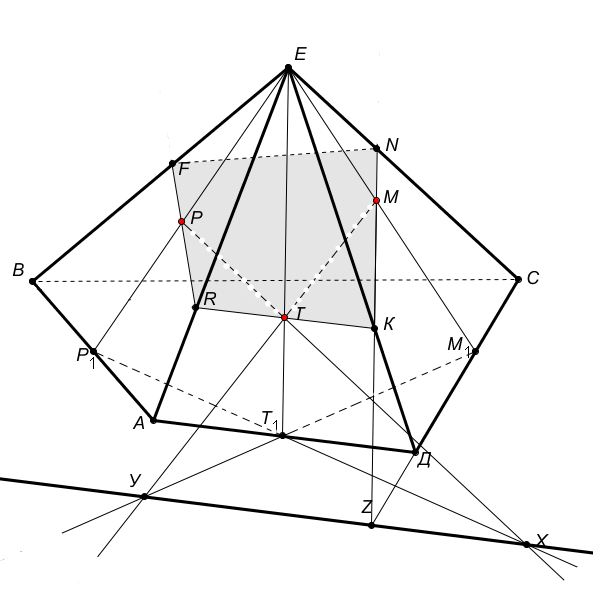
Построение	Методический комментарий
1) ЕАВСД	- строим пирамиду ЕАВСД
2) Р (ЕАВ), Т (ЕАД), М (ЕСД)	- отмечаем данные точки, лежащие в соответствующих гранях
3)	- строим проекции точек Р, Т, М на плоскость (АВСД), приняв вершину Е за центр проектирования
4) Х | Х=(РТ) ( ) 5) У | У=(МТ) ( )	- находим две точки основного следа плоскости (РТМ).
6) (ХУ) – след	- прямая (ХУ) основной след секущей плоскости (РМТ)
7) Z | Z=( Д) (ХУ)	- построим след секущей плоскости на (ЕД). Для этого найдем точку Z, в которой прямая ( Д) пересекает след (ХУ)
8) (ZМ) 9) К | К=(ZМ) (ЕД)	- проведем (ZМ) и получим точку К, в которой прямая (ZМ) пересекает (ЕД). Точка К является следом секущей плоскости на прямой (ЕД).
10) N | N=(ZМ) (ЕС)	- проведем (ZМ) до пересечения с (ЕС) и получим точку N, являющуюся следом секущей плоскости на прямой (ЕС).
11) (ТК) 12) R | R=(ТК) (ЕА)	-т.к. точки Т и К лежат в одной плоскости, то можем провести прямую (ТК). При пересечении (ТК) с (ЕА) получим точку R, являющуюся следом секущей плоскости на прямой (ЕА).
13) (RP) 14) F | F=(RP) (ЕB)	-т.к. точки R и P лежат в одной плоскости, то можем провести прямую (RP). При пересечении (RP) с (ЕB) получим точку R, являющуюся следом секущей плоскости на прямой (ЕB).
15) (FN)	-т.к. точки F и N лежат в одной плоскости, то можем провести прямую (RP).
16)	- многоугольник KNFR – искомое сечение

Возможные затруднения:

1. При выборе метода построения сечения

2. При построении основного следа

3. При нахождении точек, являющимися следами секущей плоскости на соответствующих ребрах.

59. Решить задачу.

Дано: конус, h=SO=3, r=OD=4, (O, r),

Найти:

Решение:

I. Построение:

1) АВ | АВ – хорда

2) SA, SB

3) SK | SK AB

4)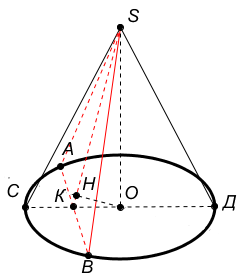 OH | OH SK

II. Доказать, что ОН=

1) SO (по условию),

SK – наклонная, ОК – проекция,

АВ , SK AB (по построению)

АВ ОК (по теореме о трех перпендикулярах)

2) SK AB (по построению),

АВ ОК (из 1)

АВ (SKO) (по признаку перпендикулярности прямой и плоскости)

АВ ОН,

OH SK (по построению)

ОН (SAB) (по признаку перпендикулярности прямой и плоскости)

ОН= (по определению расстояния от точки до плоскости)

III. Вычисления:

1) ОК - ?

Рассм SKO: SK AB, АВ ОК SKO – линейный угол двугранного угла

SO=3

2) ОН - ?

Рассм НОК: ,

Ответ:

Теоретические основы решения:

1) теорема о трех перпендикулярах

2) признак перпендикулярности прямой и плоскости

3) определение расстояния от точки до плоскости

4) определение линейного угла двугранного угла

5) определение тангенса и синуса угла

Затруднения возможны:

1) при построении сечения

2) при доказательстве ОН=

3) при решении задачи с использованием тангенса и синуса угла