- •Определение матрицы, определителя, минора, алгебраического дополнения.
- •Общие свойства определителя . Правило разложения определителя по строке (столбцу)
- •Системы линейных уравнений. Условия их совместимости, определенности, равносильности. Определение ранга матрицы.
- •Решение слау. Формулы Крамера. Метод Гаусса. Привести пример.
- •Действия над матрицами. Матричный метод решения систем линейных уравнений.
- •Линейные действия над вектором. Определение коллинеарности и компланарности векторов.
- •Исследование линейной зависимости векторов на плоскости и в пространстве.
- •Определение базиса векторов и координат вектора. Прямоугольная система координат.
- •Проекция вектора на ось. Координаты точки и вектора в прямоугольной системе.
- •Линейные действия над векторами в координатном представлении.
- •Скалярное произведение векторов. Опр., свойства , координатное представление
- •Векторное произведение векторов. Опр., свойства , координатное представление
- •Смешанное произведение векторов. Опр., свойства , координатное представление
- •Вывод уравнения окружности.
- •Вывод всех форм уравнения прямой на плоскости
- •Расстояние от точки до прямой, пересечение прямых . Вывод формул.
- •Эллипс. Вывод канонического уравнения
- •Уравнение гиперболы и ее график.
- •Уравнение параболы и ее график.
- •Преобразование координат на плоскости
- •Полярная система координат
- •Общее уравнение кривой второго порядка. Переход к каноническим уравнениям.
- •Вывод трех форм уравнения плоскости в пространстве
- •Угол между плоскостями. Расстояние от точки до плоскости
- •Вывод канонического и общего уравнения прямой в пространстве. Переход между ними.
- •Элементы теории множеств. Опр.Функции в теории множеств.
- •Способы задания функции, явная форма функции, обратная ,четная , нечетная, периодическая функция.
- •Определение основных элементарных функций
- •Определение числовой последовательности , ее предела
- •Определение бесконечно малой величины, предельного процесса, предела функции
- •Доказательства лемм о бесконечно малых, сравнение бесконечно малых.
- •Доказательства теорем о пределах
- •Три определения непрерывности функции в точке. Свойства непрерывных функций.
- •Общие правила раскрытия неопределенности
- •Определение средней скорости движения, мгновенной скорости, производной от функции. Алгебраичес1кий, физический , геометрический смысл производной.
- •Вывод формул для производных от сумм, произведения, частного двух функций
- •Сложная функция. Правило ее дифференцирования
- •Производные высших порядков. Дифференциалы высших порядков
- •Вывод формул дифференцирования степенной, показательной логарифмической, тригонометрических и обратных тригонометрических функций.
- •Производная показательной функции.
- •Производная логарифмической функции.
- •Производные тригонометрических функций.
- •Логарифмическое дифференцирование . Дифференцирование неявной функции.
- •Дифференцирование неявных функций
- •Определение дифференциала функции. Его общие свойства
- •Геометрический смысл дифференциала. Вывод
- •Производные и дифференциалы высших порядков.
- •40 Вопрос такой же
- •Вывод условий монотонного изменения функций и теоремы Ферма.
- •Вывод необходимого и достаточных условий существования экстремума.
- •Теоремы Ролля, Лагранжа, Коши, Лопиталя.
- •Определение выпуклости, вогнутости , точек перегиба графика функций и асимптоты функций.
- •Общая схема исследования функции и построение графика.
Определение основных элементарных функций
Основные элементарные функции:
постоянная у = с, с = const;
степенная у = хn, n R;
показательная у = ах, а > 0, a ≠ 1;
логарифмическая у = logax, а > 0, a ≠ 1;
тригонометрические у = Sin(x), y = Cos(x), y = tg(x), y = ctg(x);
обратные тригонометрические y = arcSin x, y = arcCos x и др.
Определение числовой последовательности , ее предела
Числовая последовательность аn – последовательность значений функции, определенных для целочисленных аргументов, т.е. аn = f(n), где n = 1, 2, 3. Всякая функция f(x), определенная на интервале (1, ), порождает свою числовую последовательность.
Предел числовой последовательности аn – число а, такое, что с ростом n разность между числом и членом последовательности становится меньше любого другого наперед заданного числа, тогда а = lim аn.
Определение бесконечно малой величины, предельного процесса, предела функции
Бесконечно малая величина – величина х, если она стремиться к нулю, делается меньше любого наперед заданного числа, но 0 так и не достигает. Процесс изменения б.м.в. называется предельным процессом.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Доказательства лемм о бесконечно малых, сравнение бесконечно малых.
Леммы о бесконечно малых.
Лемма 1: алгебраическая сумма конечного числа бесконечно малых при х а является бесконечно малой.
Лемма 2: произведение ограниченной в окрестности точки а функции на бесконечно малую при х а является бесконечно малой.
Сравнение бесконечно малых.
Пусть при х а а(х) и в(х) – бесконечно малые, тогда:
если lim (в/а) = 0, то в – бесконечно малая высш. порядка, чем а.
если lim (в/аn) ≠ 0, то в – бесконечно малая n-порядка, чем а.
если lim (в/а) = 1, то а и в – эквивалентные бесконечно малые.
Доказательства теорем о пределах
Теоремы о пределах:
lim с = с, если с – const, предел постоянной величины равен этой величине;
lim (х + у – z) = lim x + lim y – lim z, предел алгебраической суммы нескольких слагаемых равен алгебраической сумме пределов каждого из них;
lim ху = lim х lim у, предел произведения нескольких сомножи-телей равен произведению пределов каждого из них;
lim х/у = lim х / lim у, предел дроби равен пределу числителя, деленному на предел знаменателя, если знаменатель не равен 0;
lim сf(x) = c lim f(х), если с – const, постоянную величину можно вынести за знак предела;
lim хn = (lim x)n:
lim nx = nlim x.
Три определения непрерывности функции в точке. Свойства непрерывных функций.
Пусть
функция ![]() определена
на некотором интервале
определена
на некотором интервале ![]() ,
для которого
,
для которого ![]() --
внутренняя точка. Функция
называется непрерывной
в точке
,
если существует предел
при
--
внутренняя точка. Функция
называется непрерывной
в точке
,
если существует предел
при ![]() и
этот предел равен значению
и
этот предел равен значению ![]() ,
то есть
,
то есть
![]()
Пусть
функция
определена
на некотором полуинтервале ![]() ,
для которого
--
левый конец. Функция
называется непрерывной
справа в точке
,
если существует предел
при
,
для которого
--
левый конец. Функция
называется непрерывной
справа в точке
,
если существует предел
при ![]() и
этот предел равен значению
,
то есть
и
этот предел равен значению
,
то есть
![]()
Пусть,
наконец, функция
определена
на некотором полуинтервале ![]() ,
для которого
--
правый конец. Функция
называется непрерывной
слева в точке
,
если существует предел
при
,
для которого
--
правый конец. Функция
называется непрерывной
слева в точке
,
если существует предел
при ![]() и
этот предел равен значению
,
то есть
и
этот предел равен значению
,
то есть
![]()
Функция, непрерывная в точке
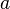 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки.Если функция
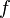 непрерывна
в точке
и
непрерывна
в точке
и 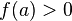 (или
(или 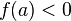 ),
то
),
то 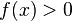 (или
(или 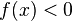 )
для всех
,
достаточно близких к
.
)
для всех
,
достаточно близких к
.Если функции и
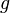 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции 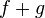 и
и  тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
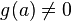 ,
то функция
,
то функция 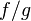 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
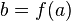 ,
то их композиция
,
то их композиция 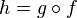 непрерывна
в точке
.
непрерывна
в точке
.
Вывод замечательного предела lim sinx/x=1 при x->0
 lim
Sinx
/ x
= 1, при х
0 Имеем окружность R
= 1 и касательные AD,
BD.
Из прямоугольных ОАС
и ОАD
следует: Sin
x
= AC/1,
tg
x
= AD/1.
Точки А и В соединяют три линии: прямая
АВ = 2АС = 2 Sin
x,
дуга АВ = 2х и ломанная ФВИ = 2АD
= 2tgx.
Из соотношения длин этих линий следует:
2Sinx
< 2x
< 2tgx.
Значит, 1 < x/Sinx
< 1/Cosx,
1 > Sinx/x
> Cosx.
При переходе в неравенстве к пределу
х0
имеем lim
Cosx
=1, 1
lim
Sinx/x
1, следовательно, lim
Sinx/x
= 1.
lim
Sinx
/ x
= 1, при х
0 Имеем окружность R
= 1 и касательные AD,
BD.
Из прямоугольных ОАС
и ОАD
следует: Sin
x
= AC/1,
tg
x
= AD/1.
Точки А и В соединяют три линии: прямая
АВ = 2АС = 2 Sin
x,
дуга АВ = 2х и ломанная ФВИ = 2АD
= 2tgx.
Из соотношения длин этих линий следует:
2Sinx
< 2x
< 2tgx.
Значит, 1 < x/Sinx
< 1/Cosx,
1 > Sinx/x
> Cosx.
При переходе в неравенстве к пределу
х0
имеем lim
Cosx
=1, 1
lim
Sinx/x
1, следовательно, lim
Sinx/x
= 1.
Натуральное число е. Вывод замечательного предела lim(1+x)^(1/x)=e при x->0
Натуральное число – основание логарифма, приводящее к высшей степени симметрии графиков показательной и логарифмической функций. Обозначается е = 2,72…
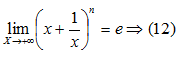
Доказательство:
Для
любого значения ![]() найдется
такое натуральное
найдется
такое натуральное ![]() ,что
будет выполняться неравенство:
,что
будет выполняться неравенство:
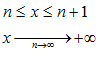
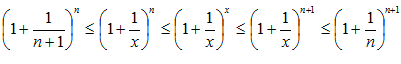
Будем пользоваться свойствами степенной и показательной функции.
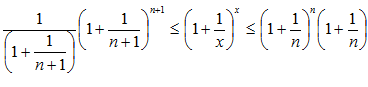
Примем теорему о сжатой переменной…ч.т.д.
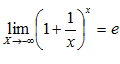
Доказательство:
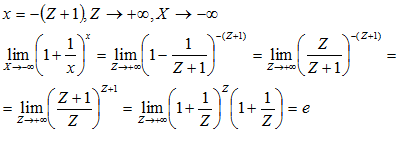 Ч.Т.Д.
Ч.Т.Д.
Формулы (11) и (12) записываются в виде однообразной формулы.