24. Угол между плоскостями. Расстояние от точки до плоскости

Пусть заданы две плоскости Q₁ и Q₂:

Под углом между плоскостями Q₁ и Q₂ понимается один из двугран­ных углов, образованных этими плоскостями.

Угол    между  нормальными  векторами     и    плоскостей Q₁ и Q₂равен одному из этих углов (см. рис. 72).

Для нахождения острого угла следует взять модуль правой части.

Если плоскости Q₁ и Q₂ перпендикулярны    (см. рис. 73, а), то таковы же их нормали, т. е.            (и наоборот). Но тогда  , т. е.  . Полученное равенство есть условие перпендикулярности двух плоскостей Q₁ и Q₂.

Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут параллельны и их нормали   и   (и наоборот). Но тогда, как известно координаты векторов пропорциональны:  . Это и есть уcловиє параллельности двух плоскостей Q₁ и Q₂.

Расстояние от точки до плоскости

Пусть задана точка   и плоскость Q своим уравнением  . Расстояние d от точки   до плоскости Q находится по формуле

Вывод этой формулы такой же, как вывод формулы расстояния от точки   до прямой .

Расстояние d от точки M₀ до плоскости Q равно модулю проекции вектора  , где   — произвольная точка плоскости Q, на н аправление нормального вектора   (см. рис. 74). Следовательно,

 

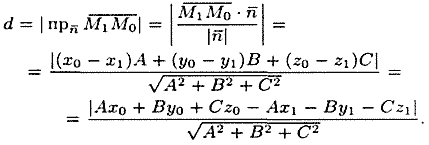
А так как точка   принадлежит плоскости Q, то

Поэтому  . Отметим, что если плоскость Q задана уравнением  , то расстояние от точки   до плоскости Q может быть найдено по формуле

  

25. Вывод канонического и общего уравнения прямой в пространстве. Переход между ними.

Пусть даны точка М ₀ и вектор  . Требуется найти уравнение плоскости, проходящей через точку М ₀ перпендикулярно вектору  . Возьмем на искомой плоскости произвольную точку М и рассмотрим   и  — радиусы-векторы точек М и М ₀. Вектор   лежит на плоскости и, следовательно, ортогонален вектору  , что равносильно векторному равенству ( – )· = 0. Полученное уравнение называется векторным уравнением плоскости. Переписав это уравнение в координатной форме, получим уравнение плоскости, проходящей через точку перпендикулярно вектору: A (x – x ₀) + B ( y – y ₀ ) + C (z – z ₀ ) = 0. В полученном уравнении x ₀, y ₀ и z ₀ — координаты точки М ₀, а А, В и С — координаты вектора  , который называется вектором нормалиплоскости.  Раскрыв скобки в полученном уравнении и обозначив число – A x ₀ – B y ₀ – С z ₀ через D, получим общее уравнение плоскости: A x + B y + С z + D = 0. В этом уравнении коэффициенты А, В и С при переменных являются координатами вектора нормали. Если А = 0, то уравнение примет вид B y + С z + D = 0, нормаль  = (0; В; C) перпендикулярна оси ОХ, а сама плоскость, следовательно, параллельна этой оси. Если В = 0, то уравнение примет вид A x + С z + D = 0, нормаль  = (А; 0; C) перпендикулярна оси ОY, а сама плоскость параллельна оси ОY. Если С = 0, то уравнение примет вид A x + B y + D = 0, нормаль  = (А; B; 0) перпендикулярна оси ОZ, а сама плоскость параллельна оси ОZ. Если D = 0, то уравнение A x + B y + С z = 0 задает плоскость, проходящую через начало координат.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую. Выберем следующий способ задания прямой линии в пространстве: укажем точку, через которую проходит прямая a, и направляющий вектор прямой a. Будем считать, что точка   лежит на прямой а и   - направляющий вектор прямой а.

Очевидно, что множество точек   трехмерного пространства определяет прямую атогда и только тогда, когда векторы   и   коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов   и   в координатной форме. Для этого нам нужно знать координаты этих векторов. Координаты вектора   нам известны из условия. Осталось вычислить координыты вектора   - они равны разности соответствующих координат точек   и  , то есть,   (при необходимости смотрите нахождение координат вектора по координатам точек). Теперь записываем условие коллинеарности векторов   и  : , где   - произвольное действительное число (при  точки   и   совпадают, что нас тоже устраивает).

Если  , то каждое уравнение системы 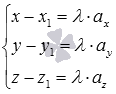  можно разрешить относительно параметра   и приравнять правые части:

Полученные уравнения вида   в заданной прямоугольной системе координат Oxyz определяют прямую a. Уравнения   есть канонические уравнения прямой в трехмерном пространстве в прямоугольной системе координат Oxyz. Их также называют уравнениями прямой в пространстве в каноническом виде.

Пример. Привести общие уравнения прямой   к каноническому виду.

 

Решение. Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например,   и решив систему уравнений   найдем  .

Нормальные векторы плоскостей, определяющих прямую, имеют координаты  ,  . Поэтому направляющий вектор прямой будет  . Следовательно,  .