20. Преобразование координат на плоскости

Преобразование координат на плоскости.

Параллельный перенос системы координат. Имеем прямоуголь-ную систему координат ХУ с центром в точке О (0, 0). Через некоторую точку О* (а, в) проведем новые оси координат, параллельные Х и У, сохранив направление и масштаб. Координаты произвольной точки М (х, у) в новой системе координат Х*У* примут значения

х* = х – а или х = х* + а

у* = у – в у = у* + в

т.е. параллельный перенос системы координат приводит к линейным преобразованиям координат.

Поворот системы координат. Систему координат ХУ с ортами i, j повернем на угол относительно начала координат и введем новые орты i*, j*. Выразим старые орты через новые

i = cos  i* - sin  j*

j = sin  i* + cos  j*

Радиус-вектор произвольной точки М (х, у) разложим по ортам i, j и перейдем от них к ортам i*, j*.

ОМ = {х, у} = хi + уj = x (cos  i* - sin  j*) + y (sin  i* + cos  j*) = (x cos  + y sin a) i* + (-x sin  + y cos ) j* = {x*, y*}

В результате получаем формулу преобразования координат при повороте осей на угол :

х* = х cos  + y sin 

y* = -x sin  + y cos 

21. Полярная система координат

Полярные координаты.

Пусть на плоскости дана точка О – полюс и луч ОР – полярная ось. Тогда положение точки М на плоскости определяет полярный угол  = МОР и радиус-вектор r = ОМ. Если полярная ось совпадает с осями координат ХУ, то

х = r Cos , y = Sin 

и обратный переход

r = x² + y², tg  = y / x.

Если полюс совпадает с фокусом эллипса, гиперболы, параболы и луч ОР направлен по оси симметрии в сторону более удаленной вершины, то уравнения всех трех кривых будут одинаковы

r = p / (1 –  Cos ),

где  - эксцентриситет, p – параметр. Для эллипса и гиперболы

p = b² / a.

22. Общее уравнение кривой второго порядка. Переход к каноническим уравнениям.

рассматривается произведение  .

• Если   , то эллипс;

• Если 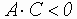  , то гипербола;

• Если   , то парабола.

Уравнение второго порядка вида   определяет на плоскости кривую. Группа членов   называется квадратичной формой,   – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.  Матрица   называется матрицей квадратичной формы. Здесь  . Чтобы матрицу   привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда  , где λ₁ и λ₂ – собственные числа матрицы B.  В базисе из собственных векторов матрицы   квадратичная форма будет иметь канонический вид:  .  Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.  Канонический вид кривой второго порядка:  , причем:  а) если λ₁>0; λ₂>0 – эллипс, в частности, при λ₁=λ₂ это окружность;  б) если λ₁>0, λ₂<0 (λ₁<0, λ₂>0) имеем гиперболу;  в) если λ₁=0 либо λ₂=0, то кривая является параболой и после поворота осей координат имеет вид   (здесь λ₂=0). Дополняя до полного квадрата, будем иметь: