1. Определение матрицы, определителя, минора, алгебраического дополнения.

Квадратная матрица порядка n – таблица чисел, состоящая из n строк и n столбцов.

Определитель матрицы (детерминатор) – число, составленное из элементов матрицы по определенному правилу.

Минор элемента a_ik определителя матрицы А – определитель, полученный из А путем вычеркивания i-ой строки и k-столбца (M_ik), т.е. определитель порядка n-1.

Алгебраическое дополнение элемента a_ik – соответствующий минор M_ik, умноженный на знаковый множитель.

A_ik = (-1)^i+k • M_ik

2. Общие свойства определителя . Правило разложения определителя по строке (столбцу)

Свойства определителя:

• величина определителя не меняется при замене строк столбцами (операция транспонирования);

• перестановка местами двух любых строк (столбцов) меняет знак определителя;

• определитель с двумя одинаковыми строками (столбцами) равен нулю;

• общий множитель элементов одной строки (столбца) можно вынести за знак определителя;

• прибавление элементов одной строки, умноженных на произвольное число, к элементам другой строки определителя не меняет.

Теорема разложения определителя: всякий определитель можно представить как сумму элементов любой строки или столбца, умноженных на соответствующие алгебраические дополнения

А = ∑ a_ik • A_ik

3. Системы линейных уравнений. Условия их совместимости, определенности, равносильности. Определение ранга матрицы.

Решение системы линейных уравнений – совокупность из n чисел x_ik, которые обращают ее в верные равенства.

Решить систему – выяснить совместна она или нет.

Совместная система – система алгебраических уравнений, имеющая хотя бы одно решение.

Определенная система – совместная система, имеющая единственное решение.

Неопределенная система – совместная система, имеющая более одного решения.

Равносильные (эквивалентные) системы – системы, имеющее одно и тоже общее решение.

Ранг матрицы – число, характеризующее наибольший порядок миноров данной матрицы, отличных от нуля.

Теорема 1: Если ранг совместной системы линейных уравнений равен числу неизвестных этой системы, то система имеет единственное решение.

Теорема 2: Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

4. Решение слау. Формулы Крамера. Метод Гаусса. Привести пример.

Решение СЛАУ матричным методом Система алгебраических уравнений может быть представлена в виде матричного уравнения  Тогда решение системы уравнений будет иметь вид: Пример решения СЛАУ Пусть дана система уравнений  . Обозначив   получаем . Вычислив  , получаем . Отсюда имеем решение СЛАУ: x = 1; y = -1; z = 2.

Решение СЛАУ методом Крамера. Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

Решение СЛАУ методом Гаусса.

Метод Гаусса: путем элементарных преобразований представить расширенную матрицу системы уравнений в треугольной форме, когда все элементы ниже главной диагонали обращены в нуль.

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при   во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на   и  , соответственно:

Теперь обнулим коэффициент при   в третьей строке, вычтя из неё вторую строку, умноженную на  :

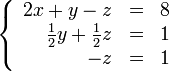
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма. На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные   и  . Таким образом исходная система решена.