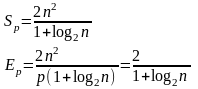- •Назвіть основні етапи розвитку паралельної обробки.
- •Що було передумовою розвитку паралелізму в програмному забезпеченні?
- •Назвіть важливі причини використання паралелізму в програмному забезпеченні.
- •Які етапи можна виділити в процесі розв’язання будь-якої задачі на паралельному комп’ютері?
- •У яких галузях виникають надскладні обчислювальні завдання?
- •Назвіть способи підвищення продуктивності комп’ютерів.
- •З якими проблемами можна зіштовхнутися під час використання багатопроцесорних систем?
- •Визначте характеристики доступних вам багатопроцесорних машин.
- •Скільки процесорів на вашій машині, і які їх робочі частоти?
- •Наскільки великий розмір кеш-пам’яті багатопроцесорних машин, як вона організована? Який час доступу?
- •Як організовано сполучну мережу?
- •Який час віддаленого доступу до пам’яті або передачі повідомлення?
- •13. Дослідіть будь-який комп’ютер. Які в нього центральній процесор, пам'ять, операційна система, форма представлення чисел?
- •Як формується закон Амдаля? Який аспект паралельних обчислень дозволяє врахувати цей закон?
- •У чому можуть полягати відмінності паралельних обчислювальних систем?
- •3.Що покладено в основу класифікації Фліна?
- •У чому полягає принцип розподілу багатопроцесорних систем на мультипроцесорні й мультикомп’ютери. ?
- •Які класи систем вам відомі для мультипроцесорів?
- •У чому полягають позитивні і негативні сторони симетричних мультипроцесори.
- •Класи систем що вам відомо для мультикомп’ютерів?
- •У чому полягаю позитивні і негативні сторони кластерних систем?
- •Які топології мереж передачі даних найчастіше використовується?
- •10, У чому полягають особливості мереж передачі даних для кластерів?
- •16. Розгляньте додаткові способи класифікації комп'ютерних систем.
- •18. Назвіть сервіси базової Grid-системи.
- •У чому полягають основні способи досягнення паралелізму?
- •2. Назвіть основні форми декомпозиції.
- •3. Что означают термины: декомпозиция задачи, декомпозиция данных, декомпозиция потоков?
- •4 Поясніть значення різних декомпозицій.
- •5 До чого призведе керування одночасними діями та їх можливою взаємодією?
- •6 Назвіть паралельні шаблони програмування й зробіть стислий огляд типів проблем, до яких може бути застосований кожний зразок.
- •7 Що являє собою розсіювання помилки? з яких кроків складається дифузний алгоритм?
- •8. Опишіть найдоцільніший підхід для паралельної реалізації дифузного алгоритму. На чому ґрунтується ефективний розподіл роботи серед потоків
- •9.Назвіть різновиди паралельної обробки
- •10. До чого зводиться задача розпаралелювання програми?
- •Як визначається модель «операції - операнди»?
- •Як визначається розклад для розподілу обчисленнь між процесорами?
- •Як визначається час виконання паралельного алгоритму
- •4. Який розклад є оптимальним?
- •6. Які оцінки слід використовувати як характеристику часу послідовного розвязання задачі?
- •7. Як визначити мінімально можливий час паралельного розв’язання задачі за графом «Операнди-операції»
- •8. Які залежності можуть бути отримані для часу паралельного розв’язання задачі у разі збільшення або зменшення кількості процесорів?
- •9. За якої кількості процесорів можуть бути отримані часи використання паралельного алгоритму зіставні за порядком з оцінками мінімально можливого часу розв’язання задачі?
- •10. Як визначається поняття прискорення та ефективності?
- •11. У чому полягае суперечнисть показникив прискорення и ефективности?
- •12. Який алгоритм е маштабованим? Наведить приклади методив з ризным ривнем маштабованости.
- •14. Якими е основни етапи проектування и розробки методив паралельних обчислень?
- •15. Яки основни вимоги моють бути забезпечени пид час розробки паралельних алгоритмив?
- •Якими є основні дії на етапі визначення інформаційних залежностей?
- •У чому полягають основні дії на етапі масштабування наявного набору підзадач?
- •У чому полягають основні дії на етапі розподілу підзадач за процесорами обчислювальної системи?
- •У чому полягає проблема розпаралелювання послідовного алгоритму підсумовування числових значень?
- •У чому полягає каскадна схема підсумовування? з якою метою розглядається модифікований варіант цієї схеми?
- •У чому полягає відмінність показників прискорення й ефективності для розглядуваних варіантів каскадної схеми підсумовування?
- •У чому полягає паралельний алгоритм обчислення всіх окремих сум послідовності числових значень?
- •Розробіть модель і виконайте оцінку показників прискорення й ефективності паралельних обчислень:
- •Наведіть характеристики топології мережі передачі даних
- •Назвіть загальну характеристику механізмів передачі даних
- •3 Характеристика передачи данных от одного процессора всем другим.
- •4Характеристики топологий коммуникационной среды
- •5Циклический сдвиг.
- •7Топология двоичного дерева.
- •8Классы эффективно реализуемых задач для топологий сети
- •9 Эффективность коммуникационных систем при циклическом сдвиге и кольцевой передаче.
- •1Концепция Linda
- •2 Барьерная синхронизация в Linda
- •3 Сильный и слабые стороны Linda
- •4 Пример перемножения матриц на Linda
- •5 Функциональные возможности pvm
- •6. Какие технологии программирования поддерживает pvm?
- •7. Базовые механизмы pvm?
- •8. Как осуществляется обмен сообщениями в системе pvm?
- •9. Требования к pvm программам
- •13. Модель dvm
- •15. Мобильность dvm-программ
- •14. Основные конструкции dvm
- •16. Модели программирования и параллелизма dvm
- •17. Возможности повышения эффективности dvm-программ
- •18. В чем заключается стандарт corba?
- •19. Из каких базовых компонентов состоит corba-спецификация?
- •20. Каким образом можно создать простую распределенную программу?
- •Как реализовано mpi?
- •Какие протоколы используются для обмена сообщениями между процессами?
- •Какое назначение библиотеки mpe?
- •Какие основные функции mpe?
- •5. Какая методика оценки эффективности вычислений?
- •6. Как создается файл регистрации?
- •7. Какие процедуры выполняются во время создания лог-файлов?
- •8. Какие способы анализа лог-файлов вы знаете?
- •9. Какая разница между форматами лог-файлов alog, clog slog?
- •10. Какой минимальный набор средств является достаточным для организации параллельных вычислений в системах с разделенной памятью?
- •11. В чем важность стандартизации средств передачи сообщений?
- •12. Что следует понимать под параллельной программой?
- •13. Какой минимальный набор функций mpi позволяет начать разработку параллельных программ?
- •17 У чому відмінність парних і колективних операцій передачі даних?
- •18 У яких ситуаціях слід застосовувати бар’єрну синхронізацію ?
- •19 Які режими передачі даних підтримуються у mpi?
- •20 Як організується неблокуючий обмін даними у mpi ?
- •21 Які колективні операції передачі даних передбачено у mpi ?
- •22 У яких ситуаціях може бути корисною упакування й розпакування даних ?
- •23 Що розуміють у mpi під комунікатором ?
- •24 Для чого може потребуватися створення нових комунікаторів ?
- •25 Що розуміють у mpi під віртуальною топологією ?
- •26 Які види топологій передбачено в mpi ?
- •27 Для чого може виявитися корисним використанням віртуальних топологій ?
- •2Какие библиотеки использует OpenMp? Их назначение.
- •3.Структура предложения с использованием распараллеливая.
- •4. Что такое раздел?
- •3. Какие циклы можно распараллелить и почему?
- •7. Для чего используется раздел reduction?
- •8. Как и для чего применяется синхронизация потоков?
- •10. Назовите основные ошибки при создании параллельной программы.
- •9.Дайте характеристику анализатора Intel vTune Performance analyzer.
- •11. Выведите на экран текстовую строку с помощью разных потоков.
У чому полягає відмінність показників прискорення й ефективності для розглядуваних варіантів каскадної схеми підсумовування?
Показатели ускорения и эффективности каскадной схемы алгоритма суммирования следующие:
Sp=T1/Tp=(n–1)/log2n,
Ep=T1/pTp=(n–1)/(plog2n)=(n–1)/((n/2)log2n),
Показатели ускорения и эффективности модифицированной каскадной схемы алгоритма суммирования следующие:
Sp=T1/Tp=(n–1)/2log2n,
Ep=T1/pTp=(n–1)/(2(n/log2n)log2n)=(n–1)/2n.
Сравнивая оценки модифицированной каскадной схемы с показателями обычной каскадной схемы, можно отметить, что ускорение для первого параллельного алгоритма уменьшилось в 2 раза, однако для эффективности модифицированного метода суммирования можно получить асимптотически ненулевую оценку снизу
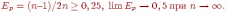
У чому полягає паралельний алгоритм обчислення всіх окремих сум послідовності числових значень?
При параллельном исполнении применение каскадной схемы в явном виде не приводит к желаемым результатам; достижение эффективного распараллеливания требует привлечения новых подходов для разработки новых параллельно-ориентированных алгоритмов решения задач. Так, для рассматриваемой задачи нахождения всех частных сумм алгоритм, обеспечивающий получение результатов за log2n параллельных операций, может состоять в следующем:
перед началом вычислений создается копия S вектора суммируемых значений (S=x);
далее на каждой итерации суммирования i, 1≤i≤log2n, формируется вспомогательный вектор Q путем сдвига вправо вектора S на
 позиций (освобождающиеся при сдвиге
позиции слева устанавливаются в нулевые
значения); итерация алгоритма завершается
параллельной операцией суммирования
векторов S и Q.
позиций (освобождающиеся при сдвиге
позиции слева устанавливаются в нулевые
значения); итерация алгоритма завершается
параллельной операцией суммирования
векторов S и Q.
Всего параллельный алгоритм выполняется за log2n параллельных операций сложения. На каждой итерации алгоритма параллельно выполняются n скалярных операций сложения и, таким образом, общее количество скалярных операций определяется величиной Kпар=nlog2n
Необходимое количество процессоров определяется количеством суммируемых значений (p=n).
С учетом полученных соотношений показатели ускорения и эффективности параллельного алгоритма вычисления всех частных сумм оцениваются следующим образом:
Sp=T1/Tp=n/log2n,
Ep=T1/pTp=n/(plog2n)=n/(nlog2n)=1/log2n.
Как следует из построенных оценок, эффективность алгоритма также уменьшается при увеличении числа суммируемых значений, и при необходимости повышения величины этого показателя может оказаться полезной модификация алгоритма, как и в случае с обычной каскадной схемой
Розробіть модель і виконайте оцінку показників прискорення й ефективності паралельних обчислень:
для задачі скалярного добутку двох векторів
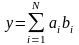
для задачі пошуку максимального й мінімального значень для заданого набору числових даних
,
для задачі пошуку середнього значення набору числових даних
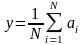
1)
К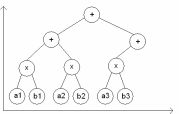 оличество
операций умножения равно
n. При последовательном
алгоритме количество операций сложения
равно n, при параллельном
-
оличество
операций умножения равно
n. При последовательном
алгоритме количество операций сложения
равно n, при параллельном
-
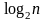 .
Поскольку считается, что время выполнения
любых вычислительных операций является
одинаковым и единичным, то
.
Поскольку считается, что время выполнения
любых вычислительных операций является
одинаковым и единичным, то
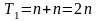 ,
,
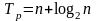 ,
p=n/2 – необходимое для выполнения
каскадной схемы количество процессоров.
,
p=n/2 – необходимое для выполнения
каскадной схемы количество процессоров.
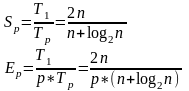
2) ,
К оличество операций сравнения равно Kпосл=(n-1) при последовательном алгоритме. При использовании параллельного алгоритма . ,
3)
Створіть модель і виконайте повний аналіз ефективності паралельних обчислень (прискорення, ефективність, максимально досяжне прискорення, прискорення масштабування) для задачі множення матриці на вектор
Задача множення матриці на вектор визначається співвідношенням:
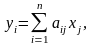
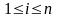
Загальна кількість скалярних
операцій оцінюється величною
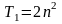
Досягнення максимально можливої швидкодії
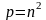
Час виконання паралельного
алгоритму визначається часом виконання
паралельної операції множення й часом
реалізації каскадної схеми:
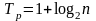
При цьому оцінки показників ефективності визначаються такими співвідношеннями: