У чому полягає проблема розпаралелювання послідовного алгоритму підсумовування числових значень?
Традиційний алгоритм для розв’язання задачі підсумовування полягає в послідовному підсумовуванні елементів числового набору
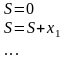
Обчислювальна схема цього алгоритму може бути подана таким чином:
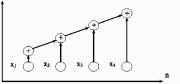
Цей алгоритм допускає тільки строго послідовне виконання і не може бути розпаралеленим. Паралелізм алгоритму стає можливим тільки при іншому способі побудови процесу обчислень. У даному випадку можна використати асоціативність операції додавання. Новий варіант підсумовування полягає у наступному:
На першій ітерації схеми всі вихідні дані розбиваються на пари, і для кожної пари обчислюється сума значень
Далі всі отримані суми пар також розбиваються на пари, і знову виконується підсумовування значень пар
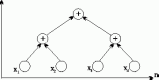
У чому полягає каскадна схема підсумовування? з якою метою розглядається модифікований варіант цієї схеми?
Каскадная схема суммирования состоит в следующем:
на первой итерации каскадной схемы все исходные данные разбиваются на пары, и для каждой пары вычисляется сумма их значений;
далее все полученные суммы также разбиваются на пары, и снова выполняется суммирование значений пар и т.д.
Количество итераций каскадной
схемы оказывается равным величине
,
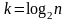а общее количество операций суммирования
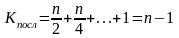совпадает с количеством операций
последовательного варианта алгоритма
суммирования. При параллельном исполнении
отдельных итераций каскадной схемы
общее количество параллельных операций
суммирования является равным
Поскольку считается, что
время выполнения любых вычислительных
операций является одинаковым и единичным,
то
,
,
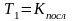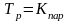поэтому показатели ускорения и
эффективности каскадной схемы алгоритма
суммирования можно оценить как:
Sp=T1/Tp=(n–1)/log2n,
Ep=T1/pTp=(n–1)/(plog2n)=(n–1)/((n/2)log2n),
где p=n/2 есть необходимое для выполнения каскадной схемы количество процессоров.
Получение асимптотически
ненулевой эффективности может быть
обеспечено, например, при использовании
модифицированной каскадной схемы. Для
упрощения построения оценок можно
предположить
,
.
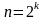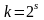Тогда в новом варианте каскадной схемы
все вычисления производятся в два
последовательно выполняемых этапа
суммирования:
на первом этапе вычислений все суммируемые значения подразделяются на (n/log2n) групп, в каждой из которых содержится log2n элементов; далее для каждой группы вычисляется сумма значений при помощи последовательного алгоритма суммирования; вычисления в каждой группе могут выполняться независимо друг от друга (т.е. параллельно – для этого необходимо наличие не менее (n/log2n) процессоров);
на втором этапе для полученных (n/log2n) сумм отдельных групп применяется обычная каскадная схема
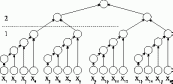
Тогда для выполнения первого этапа требуется log2n параллельных операций при использовании p1=(n/log2n) процессоров. Для выполнения второго этапа не обходимо log2(n/log2n)log2n параллельных операций для p2=(n/log2n)/2 процессоров. Как результат, данный способ суммирования характеризуется следующими показателями:
Tp=2log2n, p=(n/log2n).
С учетом полученных оценок показатели ускорения и эффективности модифицированной каскадной схемы определяются соотношениями:
Sp=T1/Tp=(n–1)/2log2n,
Ep=T1/pTp=(n–1)/(2(n/log2n)log2n)=(n–1)/2n.