Передаточная функция типовой одноконтурной системы

С

татическими называются такие САУ, у которых при постоянном задающем воздействии ошибка в установившемся режиме стремится к некоторой постоянной неравной нулю.

Часто при расчете систем передаточные функции и уравнение динамики записывают не для управляемой величины х, а для сигнала ошибки

,

который также может рассматриваться как сумма двух составляющих:

,

где е_в, е_з – составляющие сигнала ошибки, обусловленные изменениями соответственно возмущающего и задающего воздействий.

Для каждой составляющей сигнала ошибки можно записать передаточные функции, связывающие эти составляющие с соответствующими внешними воздействиями.

Передаточная функция системы по задающему воздействию равна

,

а

передаточная функция по возмущающему воздействию

Уравнение динамики системы, записанное для сигнала ошибки, будет иметь вид

Рассмотрим для примера следующий случай: пусть .

Тогда ошибка будет зависеть только от задающего воздействия

.

Пусть для нашего случая , тогда

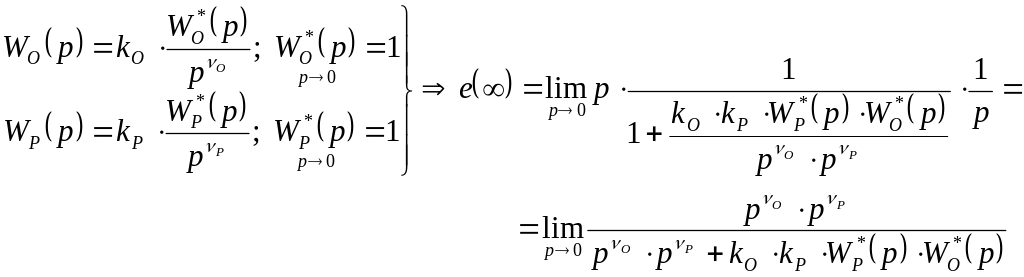
Здесь _О является порядком астатизма у объекта, а _Р – у регулятора, причем если _О0 и _Р0, то ошибка будет равна нулю.

Если регулятор или объект содержат интегрирующие звенья, то ошибка в установившемся режиме будет равна нулю, следовательно, система является астатической.

Статической будет та САУ, в которой ни регулятор, ни объект не будут содержать интегрирующих звеньев. Кроме того, статическая САУ – это САУ имеющая нулевой порядок астатизма.

Ошибки статических и астатических систем при типовых задающих воздействиях

Рассмотрим три типа задающих воздействий:

1

. х_З1=А₀1(t)

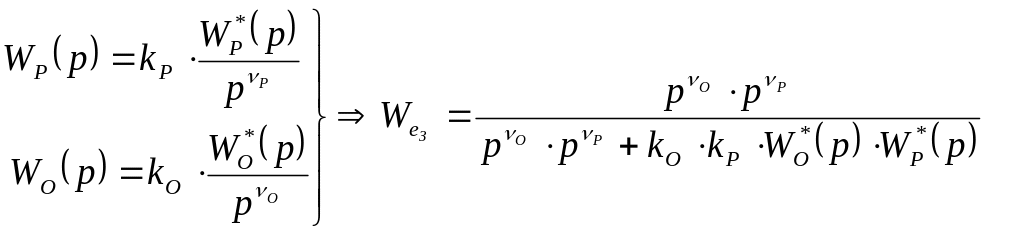
Зададим: .

Тогда .

Это означает, что, если =0, то ошибка будет равна , следовательно, система статическая, а если =1, то ошибка - , значит данная система – астатическая. Т.о. при порядке астатизма системы 1, система при данном возмущающем воздействии является астатической.

2

. х_З1=А₀t1(t)

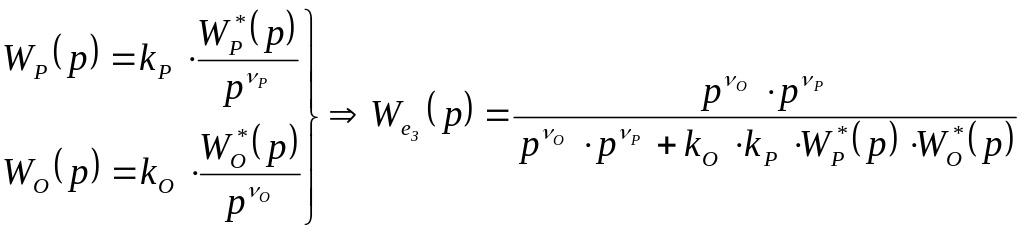
Зададим: .

Тогда .

Это означает, что, если =0, то ошибка будет равна , следовательно, система находится в неопределенном состоянии; если =1, то ошибка - , значит данная система статическая; а если =2, то ошибка равна , что говорит об астатичности данной системы. Т.о. при линейном изменяющемся задающем воздействии, система будет статической при порядке астатизма системы =1, а при 2 – система является астатической.

3

. х_З1=А₀t²1(t)

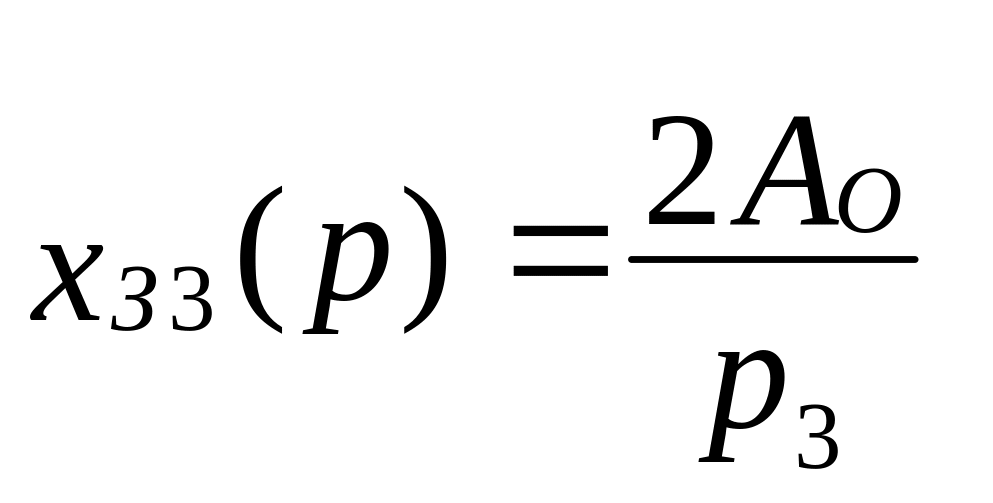
Тогда .

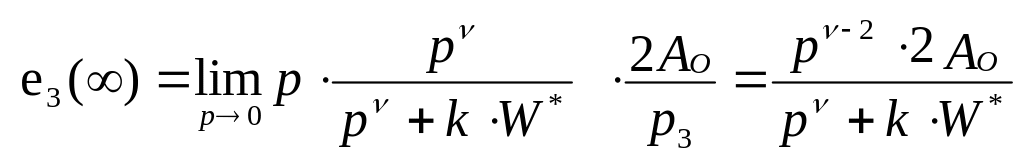Это означает, что:

• если =0, то ошибка будет равна 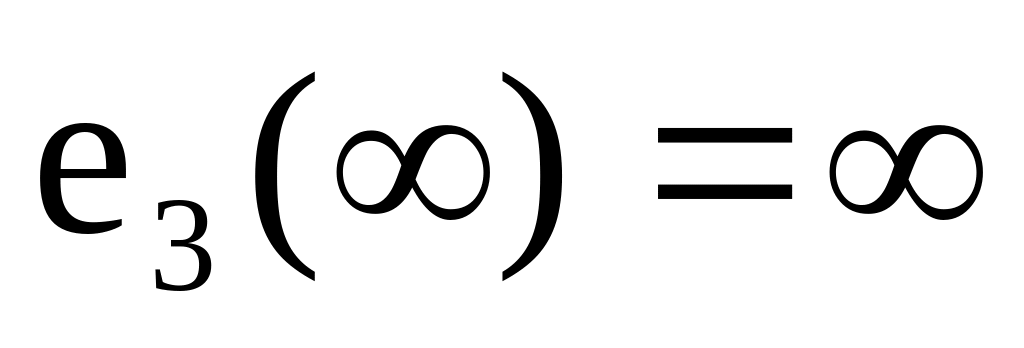, сле­довательно, система находится в неопределенном состоянии;

• если =1, то ошибка - , следовательно, система находится в неопределенном состоянии;

• если же =2, то ошибка равна 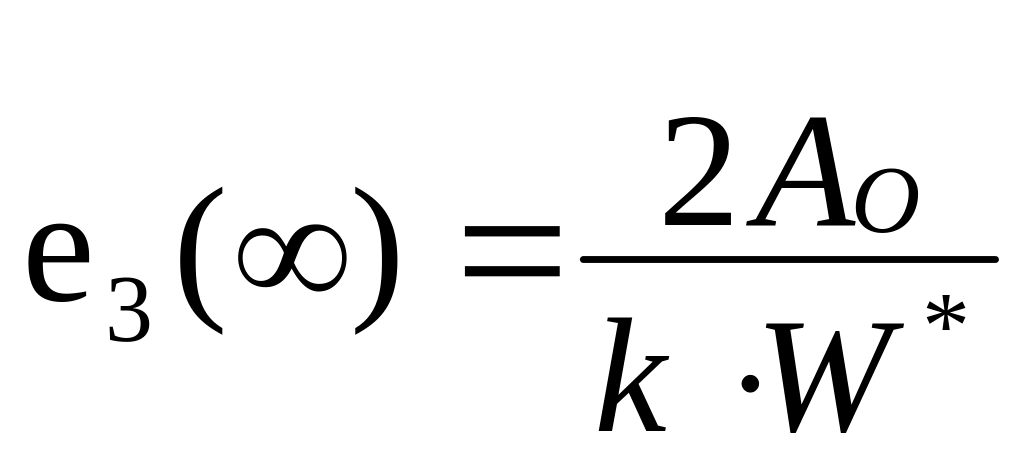, значит данная система статическая;

• если =3, то ошибка равна 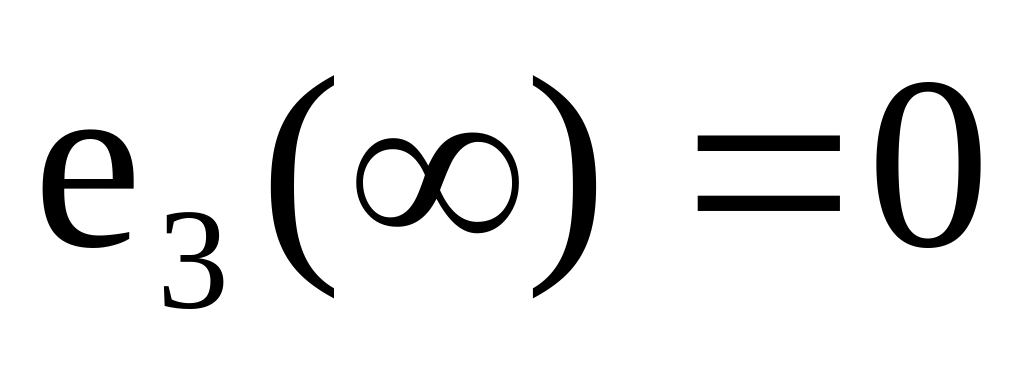- в этом случае система является астатической.

Т.о. система будет статической при порядке астатизма системы =2, а при 3 она является астатической.

Графики в этом случае аналогичны пункту 2.

Ошибка при возмущающем воздействии, не равном нулю

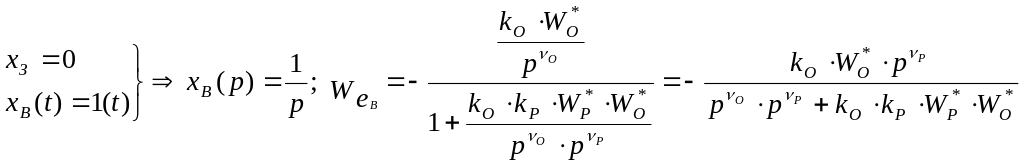
На ошибку, обусловленную возмущающим воздействием влияет только астатизм регулятора.

Таблица

Составляющие сигналов ошибки	Порядок астатизма	Виды возмущений
		А01(t)	А0 t1(t)	А0t21(t)
e3	=0	А0/(1+k)		
	=1	0	А0/ k	
	=2	0	0	2 А0/ k
eB	0=0; p=0	А0 k 0/(1+ k)		
	0=0; p =1	0	А0/ kР	
	0=1; p =0	А0 k 0/ k		
	0=1; p =1	0	А0/ kР	
	0=2; p =2	0	0	2 А0/ kР

Выводы:

1. Составляющая ошибки, обусловленная задающим воздействием, зависит от порядка астатизма всей системы

2. Составляющая ошибки, обусловленная возмущающим воздействием, зависит от порядка астатизма регулятора.

3. Ошибка при задающем воздействии определяется по формуле: е_З=А₀q!/k , где х_з= A₀t^q1(t) , q определим при q от 1 до n.

4. Ошибка при возмущающем воздействии обратно пропорциональна коэффициенту системы е_В=1/k.

5. Если q, то е_З()=,е_В()=.

6. Если q_Р, то е_З()=0,е_В()=0.

Если система работает на отслеживание ошибки, обусловленное задающим воздействием, то такая система называется системой стабилизации.

Если система работает на отслеживание ошибки, обусловленное возмущающим воздействием, то такая система называется следящей системой.