IV.2.3. Аналітичні мережі (польові роботи)

Аналітичні мережі, як і тріангуляція - мережі трикутників. Як відомо, існує ще одна побудова, що будується у вигляді трикутників, які межують один

3 одним. У такій мережі кути трикутників не вимірюються, а будуються під час створення робочої основи мензульного знімання. Така мережа називається геометричною. Ми розглянемо мережу трикутників, у яких кути вимірюються. Тому часто в геодезичній літературі такі мережі називають робочими (знімальними) мережами, що будуються методом тріангуляції. Проте, щоб відрізняти ці мережі від геометричної мережі та від тріангуляції, цілком виправдано називати їх аналітичними мережами.

Довжини сторін трикутників аналітичної мережі значно коротші, ніж у тріангуляції (min - 150 м; max - 2 км). Кути не менші за 20°. Кути вимірюються

446

Розділ IV

двома круговими прийомами теодолітами (точності, не нижчої за ЗО") з перевстановленням лімба через 90°. Допустима нев'язка трикутника не більша за 1,5'. Найчастіше використовуються такі аналітичні побудови:

1) геодезичний чотирикутник (рис. IV.2.3, а):

2) вставка в кут (рис. IV.2.3, б):

3) центральна система (рис. IV.2.3, в):

4) ланка трикутників з двома вихідними сторонами (рис. IV.2.3, г):

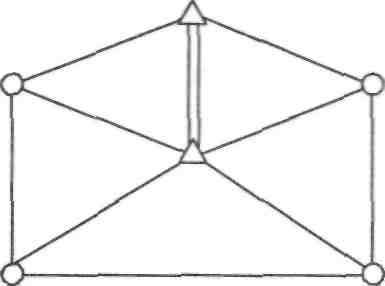
A D М

5) ланка між стороною й пунктом (рис. IV.2.3, д):

447

Великомасштабне топографічне знімання

6) ланка, побудована на стороні (рис. IV.2.3, є):

IV.2.4. Розрахунок точності ланки трикутників аналітичної мережі

Нехай під дією похибок dS_{ у довжині сторони 5 та в дирекційному куті Joe, точка Р змістилась у положення Р" на величину q . Це зміщення можна розкласти на dS_{ - уздовж лінії S_l й на г - перпендикулярно до S_x.

Рис. IV. 2.4. До визначення похибки у положенні точки Р, що визначається прямою засічкою

Із трикутника Р Р' Р" маємо:

Із трикутника N Р Р" (рис. IV.2.4.):

На підставі (IV.2.5) (IV.2.6) запишеться так:

(IV.2.5) (IV.2.6)

(IV.2.7)

448

Розділ IV

Переходячи від диференціалів до квадратичних похибок, отримаємо:

(IV.2.8)

Як відомо, у ланках трикутників сторони визначаються з відносними похибками, що описуються формулою

(IV.2.9)

Переходячи до абсолютної похибки та нехтуючи похибкою в базисі b, одержимо:

«І, =\s}^{ctg% +ctg% +ctg^ctg^}. (IV.2.10)

Крім того, як відомо

т_щ=т_у^-. (IV.2.11)

Формулі (IV.2.8) можна надати вигляду:

(IV.2.12)

або

(IV.2.13)

Припустимо, що аналітична ланка складається з рівносторонніх три­кутників:

Тоді вираз формули (IV.2.13), що в дужках, буде дорівнювати 2. Тому формулі (IV.2.13) можна надати простішого вигляду:

(IV.2.14)

Якщо діють переважно випадкові похибки, тоді їхнє накопичення буде пропорційне до yjn , де п - кількість трикутників ланки.

Похибка кінцевої точки ланки визначиться за формулою

М_Р =1,15^ S>[n. (IV.2.15)

449

Р

Великомасштабне топографічне знімання

Розрахуємо максимально допустиму кількість трикутників у ланці. Як відомо, гранична похибка в розташуванні робочої основи відносно найближчих пунктів геодезичної основи на плані - 0,2 мм. Для масштабу 1:5000 0,2 мм становить 1 м. Підставивши в (IV.2.15) замість М_Р 1 м і розв'язавши цю

формулу відносно одержуємо:

(IV.2.16)

Нехай сторони мережі дорівнюють 1000 м, а похибка вимірювання кута Тоді

п= 16 трикутників.

Для масштабу 1:2000 на плані 0,2 мм відповідає 0,4 м, тобто М_Р = 0,4 м. Тому для такого масштабу, прийнявши S - 500 м, отримаємо:

«=10 трикутників.

Наші розрахунки зроблені для висячої ланки трикутників. Якщо ланка спирається на дві вихідні сторони, то максимальна похибка буде всередині

ланки і кількість трикутників такої ланки можна збільшити в раза.

Тоді отримаємо: для масштабу 1:5000 п = 22 трикутники;

для масштабу 1:2000 п = 14 трикутників.

Інструкція [5] допускає відповідно 20 та 17 трикутників.

Як бачимо, хоча наші розрахунки спрощені, похибки вихідних даних не враховані, але одержана кількість трикутників ланки майже така сама, що і допускається інструкцією.

IV.2.5. Спрощені способи зрівноваження аналітичних мереж

І. Висяча ланка ув'язує тільки кути трикутників. Поправки в окремий

кут де - нев'язка трикутника. Далі розв'язуються трикутники і

обчислюються дирекційні кути та довжини сторін. Координати кожної точки мережі обчислюються два рази, з контролем (за двома сторонами трикутника). За кінцеві значення координат беруть середні значення.

450

Розділ IV

II. Ланка між вихідними сторонами:

1. Ув'язуються всі кути.

2. Вибирається середня лінія, наприклад CD (рис. IV.2.3, г).

3. Координати точок С і D обчислюються два рази, як у висячої ланки. Знаходять середнє з них.

4. Надалі по кожному з чотирьох ходів між точками AD , ВС, NC, MD виконуються обчислення, як у теодолітних ходах.

III. Ланка трикутників між двома пунктами (побудована на вихідній стороні) (рис. IV.2.5):

1. Ув'язуються кути у трикутниках.

1. Вибирають ходову лінію (див. рис. IV.2.5), показану пунктирною ламаною лінією і ув'язують кути за ходовою лінією. Якщо, наприклад, кількість

кутів, враховуючи ті, що межують, дорівнює п, а нев язка /о , то поправки —

п

вводяться тільки в ходові кути. До того ж, у ліві кути поправки додаються, а від

правих віднімаються.

3. У трикутниках знову з'являються нев'язки. Для ліквідації нев'язок в

інші (не ходові кути) вводяться поправки . Якщо кут [3] з отримав поправку , тоді кожний із кутів Р[! та (3[ 2 повинен одержати поправку, що дорівнює

4. За кінцево ув'язаними кутами обчислюють дирекційні кути ходових ліній та координати всіх точок, зокрема точки N . Отже, отримують координати X' та Y' точки N. Оскільки координати X' та Y' точки ./V не збігаються з відомими координатами точки N, то одержимо рис. IV.2.6.

ABE Рис. IV.2.5. До зрівноваження аналітичної мережі, побудованої на стороні AN

451

Великомасштабне топографічне знімання

Рис. IV.2.6. Редукування мережі поворотом на da

та зміною масштабу на

5. Знаходять:

Обчислюють: da = а - а' (поворот мережі). Поздовжній зсув t = S — S'.

Поперечний зсув и = S' —.

(IV.2.17) (IV.2.18) (IV.2.19)

(IV.2.20)

Коефіцієнт k =

Усі дирекційні кути ходових сторін змінюють на da . Усі обчислені сторони множаться на коефіцієнт к .

6. Ще раз обчислюють координати усіх точок за ходовою лінією за виправленими ос,- та S_t.

Якщо ланка побудована між вихідною стороною та відомим пунктом, то ув'язування мережі виконується, як і в попередньому випадку.

452

Розділ IV