11.7.4. Суть паралактичної полігонометрії

Траверсна полігонометрія з вимірюванням ліній підвісними мірними приладами потребує значних затрат праці. Тому, коли ще не було світло-віддалемірів, пошуки нових, посередніх методів вимірювання ліній були дуже актуальною науковою проблемою.

Як відомо, оптимальна довжина ліній полігонометрії 4 класу 500 м, а максимальна - 3 км. Враховуючи, що допустима довжина ходу 14 км, то для довжини ліній 1000 метрів у ході буде 14 сторін. Розрахуємо необхідну точність вимірювання ліній ходу з такими сторонами. Скористаємося відомою розра­хунковою формулою для висячого ходу:

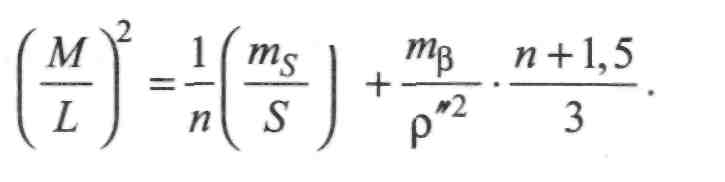
\2 »2

(Н.7.20)

У правій частині (ІІ.7.20) перший та другий члени є складовими відносної похибки — висячого ходу, викликаними відповідно похибками вимірювання ліній та кутів. За умови рівності цих двох членів можна записати:

або

М_v2(Щ

(т ^ Розв'яжемо (П.7.21)відносно ——

(П.7.21)

(ІІ.7.22)

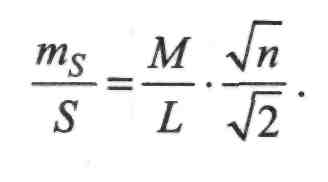
279

Розділ II

Оскільки для 4 класу полігонометрії

= 14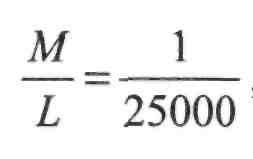

то для п

отримаємо:

S 10000

Жодний оптичний віддалемір не дає такої точності для S = 1000 м. У

1836 р. проблема швидкого визначення була успішно вирішена В.Я. Струве,

який запропонував паралактичну ланку полігонометрії. Головна відмінність

відомої вже полігонометричної ланки з коротким базисом (з горизонтальною

рейкою, завдовжки 2-3 м) і паралактичною ланкою в тому, що в цій ланці

застосовують значно довший базис, виміряний мірними дротами. Така ланка

показана на рис. ІІ.7.6.

Рис. 11.7.6. Панка паралактичної полігонометрії Розрахуємо спочатку необхідну величину паралактичного кута. Оскільки

(ІІ.7.23)

якщо т" =2", можна записати:

(П.7.24)

10000 ф*

А тому ф*= 20000", або ф°= 5,6°. Залишається знайти необхідну довжину базису Ь. Відповідно до (ІІ.7.2):

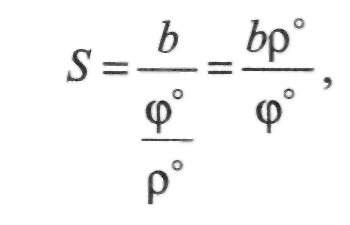
або

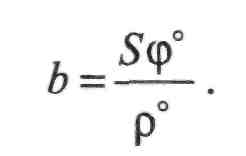
(П.7.25)

280

Планові геодезичні мережі

Тоді для S ■ 1000 м, матимемо:

Отже, для довжини мірного дроту 1₀ = 24 м достатньо буде відкласти чотири мірні дроти. Під час вимірювання ліній завдовжки 1000 м у траверсній полігонометрії необхідно буде відкласти у створі більше ніж 40 дротів. Звідси зрозуміло, як істотно зменшаться затрати часу, якщо використовувати паралактичні ланки навіть при тому, що ще потрібно в кожній ланці точно вимірювати кути.

Як очевидно з розрахунків, точність полігонометричної ланки В.Я. Струве залежить від величини кутаф. Проте для збільшення кута ф необхідно збіль­шувати довжину базису. У зв'язку з цим професор А.Д. Моторний запропо­нував [17] ланку полігонометрії, у якій базис розташовано не перпендикулярно до лінії, а вздовж лінії, тобто базис є частиною лінії, що визначається. Для однакових довжин базисів, але довших перпендикулярів (які не вимірюються), така ланка дає змогу збільшити кути ф і отримати значно вищу точність

визначення S. Для однакових за довжиною базисів та величин кутів ф, навпаки, точність ланки Струве дещо вища.

11.7.5. Суть віддалемірно-базисної полігонометрії

Віддалемірно-базисна полігонометрія - це поєднання віддалемірних визначень базисів з паралактичними ланками. Такий метод дуже еластичний і може застосовуватись у найважчих топографічних умовах. Як видно з рис. ІІ.7.7, базис Ь може бути виміряний мірним дротом, якщо лінії ходу S_x, S₂, S₃ - довгі, більші за 1 км або частіше, методом короткобазисної полігонометрії (Ь= 2-3 м), якщо лінії 5, - короткі (50-100 м). Знайшовши з паралактичної ланки довжину BN = d, далі, розв'язуючи трикутники ANB, BNC, визначають довжини сторін ходу S_l, S₂ тощо.

Виникає питання про найвигідніше співвідношення між Ь, d та S . Тео­ретичними дослідженнями доведено, що найвигіднішими, тобто найточнішими будуть ланки, коли виконується рівність

(П.7.26)

При цьому повинні бути наближено однакові кути

281

Розділ II

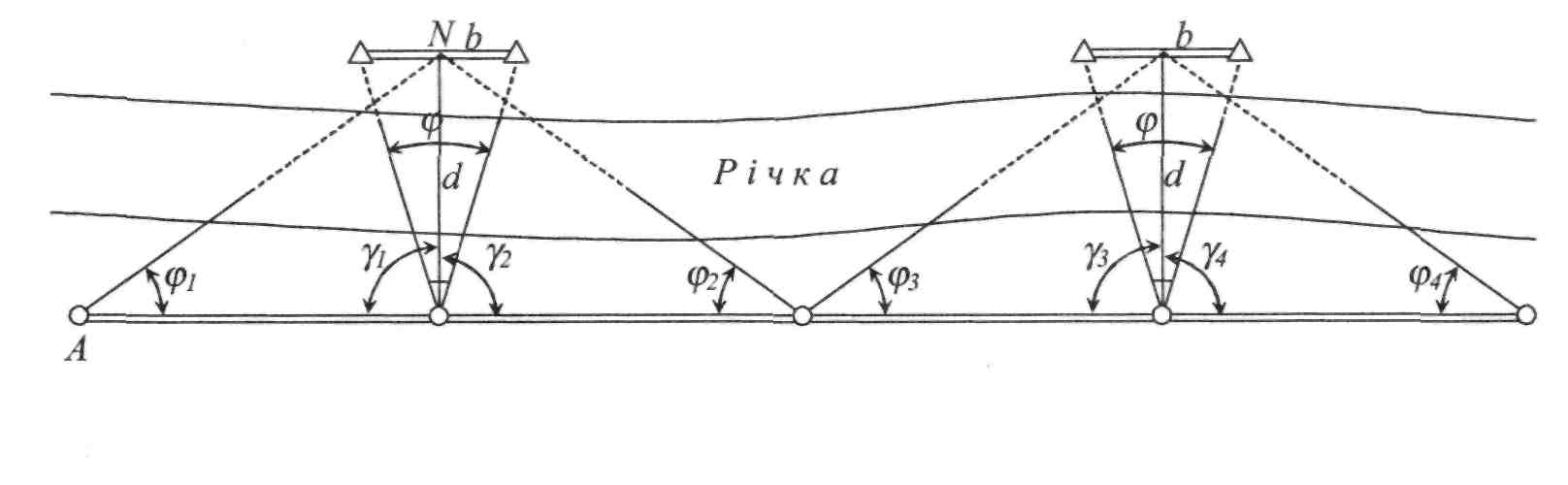
S/ В S2 C S? S4

Рис. 11.7.7. Ланка віддалемірно-базисноїполігонометрії

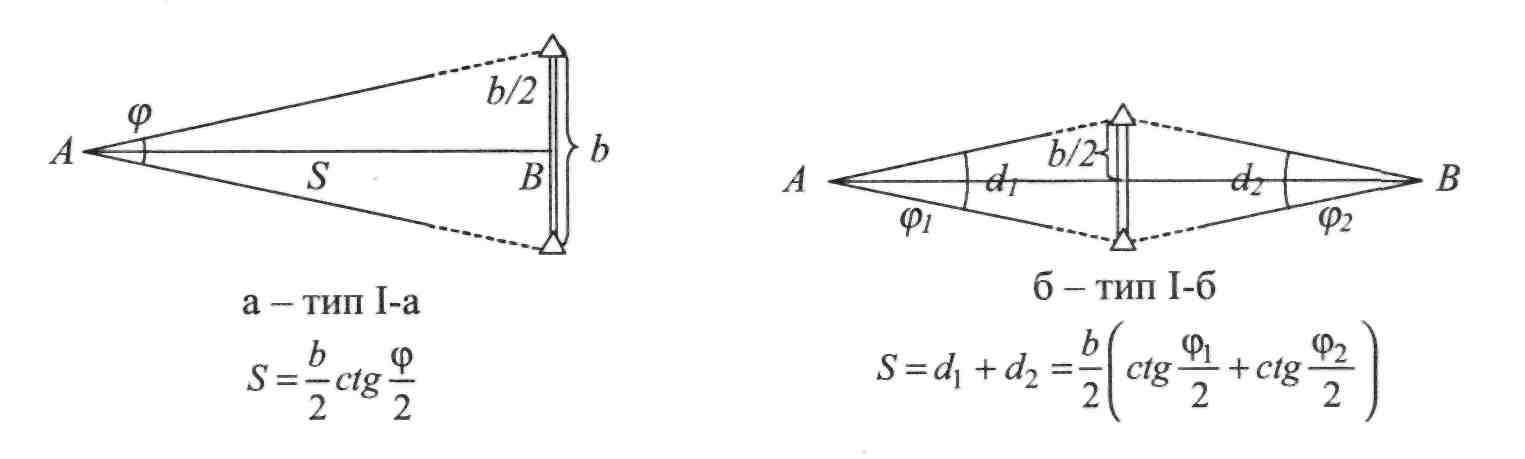
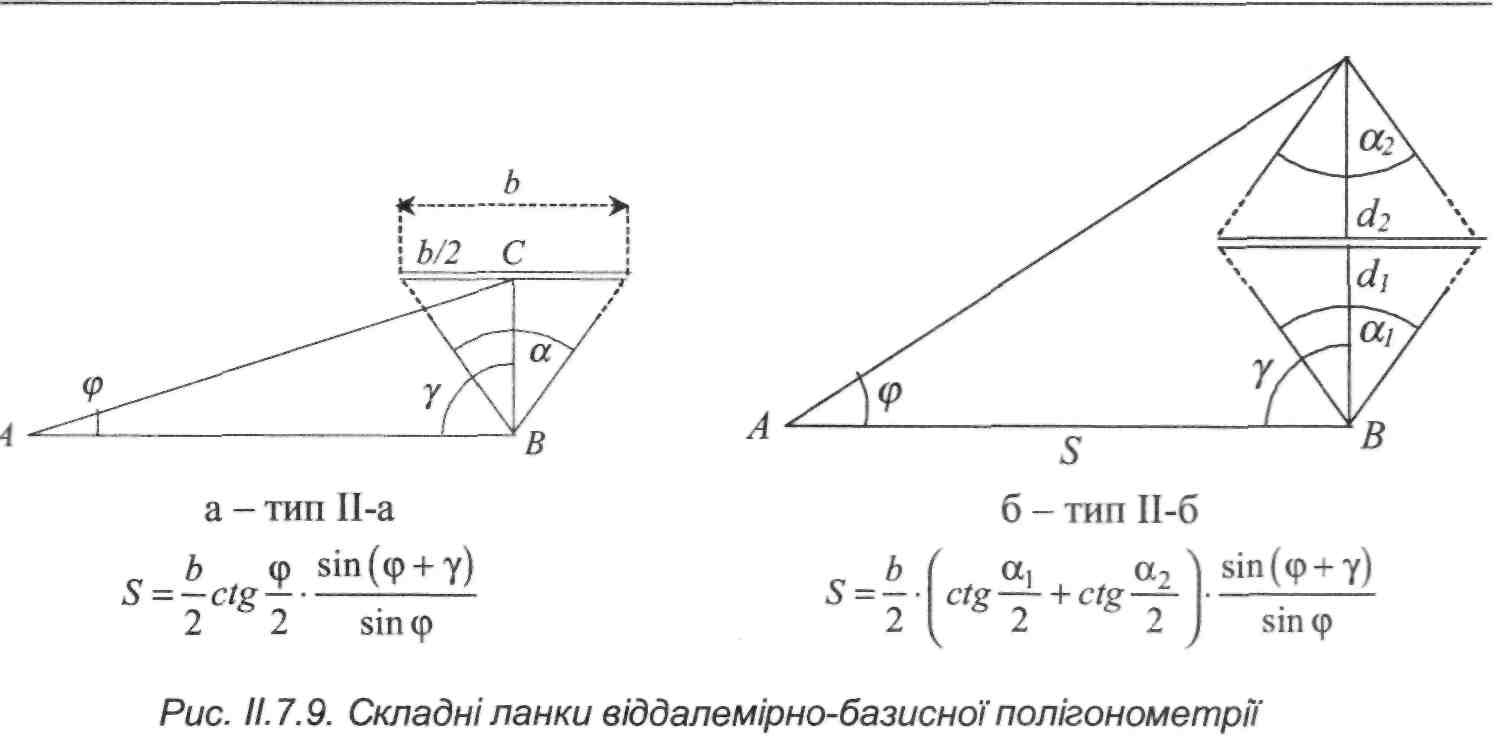
II. 7.6. Типи паралактичних і віддалемірно-базисних ланок

Паралактичні ланки поділяються на прості та складні. Подамо деякі типи ланок, що можуть бути застосовані у разі відсутності у виконавця робіт світловіддалемірів.

282

Планові геодезичні мережі

11.8. Строге зрівноваження полігонометричних ходів

11.8.1. Недоліки спрощених методів зрівноваження

Згадаємо, як ми виконували обчислення координат теодолітного ходу, прокладеного між точками з відомими координатами, а також відомими початковим і кінцевим дирекційними кутами.

Аналогічно можна виконувати обчислення координат полігонометричного ходу. У теодолітному ході ми спочатку знаходили кутову нев'язку за формулою

п+1 л+1

де £ Р і X Рш ~ відповідно практична і теоретична сума кутів ходу. Потім

(ІІ.8.1)

вводили поправки у виміряні кути. Сума поправок у кути Ida. \ повинна дорівнювати нев'язці з оберненим знаком:

(ІІ.8.2)

Це перша умова, яку має задовольняти виправлення кутів.

Потім за виправленими (зрівноваженими) кутами ми знаходили дирек-ційні кути сс_г, а, маючи ще і виміряні довжини 5,-, визначали прирости коор­динат

Ax_t = S_t ■ cos ос,; Ay_t = S, • sin ос,. (ІІ.8.3)

283

Розділ II

Далі окремо (незалежно від кутів) зрівноважували прирости координат. Спочатку знаходили нев'язки за відомими формулами

(II. 8.4)

(ІІ.8.5)

Нев'язки розподіляли в прирости координат, виконуючи ще дві умови: суми поправок у прирости абсцис та ординат [й?Лх₍] та [rfAy,] повинні дорів­нювати нев'язкам /_х і f з оберненим знаком:

(ІІ.8.6) (II. 8.7)

За виправленими (ув'язаними) приростами знаходили координати вершин ходу Х_і і Y_i. Здається, ніби три геометричні умови, що виникають у такому ході, виконані введенням поправок J(3_; в кути radAx_t, dAy_t - у прирости координат. Ось ці три умови, записані у вигляді рівнянь:

і

п

умова абсцис Х_к = Х_п + ]£ &х ',

у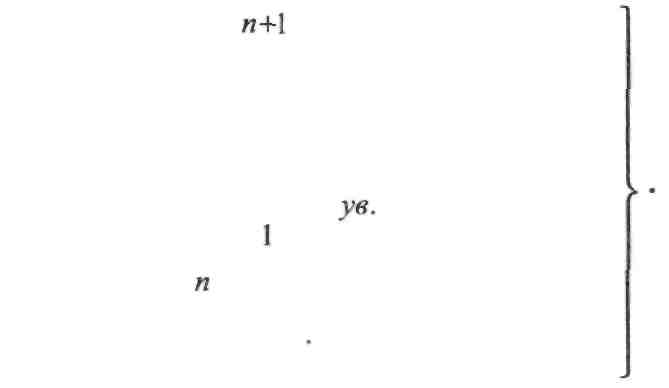 мова дирекційних кутів а_к =ос„ + ХРл^в.-180(и + і);

(П.8.8)

умова ординат Y_K = Y„ + X &у_ув

і

У (II.8.8) прийняті позначення: - ліві (стосовно напрямку ходу),

ув'язані кути повороту; - ув'язані прирости координат; а_п, а_к-

задані початковий і кінцевий дирекційні кути; - задані координати

початкової точки ходу; - координати кінцевої точки.

Але ці три умови (рівняння) розв'язувалися окремо.

Спочатку виконана умова , а потім, тільки після обчислення

приростів координат, виконано умови: Ці три геомет-

ричні умови взаємозалежні. Справді, зміна р\ кутів ходу викличе зміну довжин сторін ходу Sj. А це не враховано. Три рівняння потрібно розв'язувати разом. Тому, фактично, три геометричні умови, що виникають у ході, не задовольняються.

284

Планові геодезичні мережі

Щоб впевнитися в цьому, будемо за розрахованими нами координатами розв'язувати обернені геодезичні задачі, тобто знаходити довжини ліній S-, а також дирекційні кути а,', а потім кути повороту (3^. Тоді виявиться, що

, тобто ні ув'язані кути не будуть такими, як

виправлені поправками (d$_t) кути р,'; ні обчислені за координатами довжини ліній S'j не будуть такими, як виміряні S_t. Це означає, що знайдені координати не є такими, що задовольняють геометричні умови ходу, не є найімовірнішими.

У цьому і полягають недоліки спрощених методів зрівноваження. Вказані недоліки виникають через те, що ми не враховували залежностей між лініями та кутами. Потрібно поправки в кути та лінії шукати з одночасного розв'язання трьох геометричних умов, що виникають у ході.

Такі зрівноваження, коли знаходять поправки у кути та лінії з одночасного розв'язання умовних рівнянь, називаються строгими (точними). Накладається додаткова умова: сума квадратів поправок у кути та лінії повинна дорівнювати мінімуму [W] = шіп. До того ж обґрунтовано вибираються ваги вимірів кутів

та ліній.

Існують два методи строгого зрівноваження (вирівнювання) геодезичних ходів та мереж: корелатний та параметричний. Ці методи детально розгля­даються в теорії ймовірностей. Практичне застосування названих методів у геодезії, передусім у полігонометрії, буде висвітлено далі.

11.8.2. Кількість вимірів та невідомих у полігонометричному ході. Необхідні та надлишкові виміри

Нехай маємо полігонометричний хід, прокладений між "твердими" (відо­мими) пунктами, показаний на рис. П.8.1.

Рис. 11.8.1. Полігонометричний хід, прокладений між відомими пунктами та дирекційними кутами

У ході виміряно п ліній та (я +1) кутів. Кутів у ході завжди на один біль­ше ніж ліній, якщо виміряні також і кути (3j тар\,₊₁, що межують з лініями

285

Розділ II

тріангуляції. Отже, усього вимірів: (га + 1) + га = 2я + 1. Невідомими є координати пунктів ходу, показаних кружками. їх у ході завжди на одиницю менше ніж ліній. Невідомих абсцис Х_{ - (п -1). Невідомих ординат Y_t - (га -1) . Усього невідомих (га -1) + (и -1) = 2га - 2 .

Знайдемо кількість надлишкових вимірів: {2га + і}-(2и-2) = 3. Отже, в

полігонометричному ході, який прокладений між відомими пунктами, завжди є три надлишкові виміри. Вони не є "непотрібними". Саме надлишкові виміри приводять до того, що в ході виникають геометричні умови, про які йшлося вище. Завжди в ході або мережі кількість умов дорівнює кількості надлишкових вимірів.

Знайдемо у наведеному ході "надлишкові" виміри, тобто такі виміри, які можна було б не робити, а всі невідомі координати пунктів знайти. Якщо обчислювати координати точок від початкової точки Т_поч, тоді знайдемо координати всіх точок, зокрема Х_п, Y_n точки Р_п без вимірів кутів (3„, Р_л+1 та лінії S_n . Якщо, навпаки, обчислювати координати точок від кінцевої точки Т_кін , тоді знайдемо координати всіх точок, зокрема Х₂ , Y₂ точки Р₂ без вимірів кутів (3], Р₂ ^та ліній S .

Нарешті, можна частину точок обчислити від початку ходу, а частину -від кінця ходу. Тоді надлишковими будуть, наприклад, два кути й одна лінія, позначені на рис. II.. 1 хрестиками.

Надлишкові вимірювання спонукають до контролю вимірів і можливості зрівноваження ходів або мереж. За відсутності "надлишкових" вимірів хід перетворюється на "висячий" (спирається тільки на один відомий пункт), унеможливлюється контроль вимірів та зрівноваження ходів. Зрозуміло, що зникають і геометричні умови, що виникають у ході чи мережі.

Тому надлишкові виміри є дуже важливими.

11.8.3. Виведення формул, що зв'язують поздовжній та поперечний зсуви ходу з нев'язками по осях координат

На рис. ІІ.8.2 показано витягнутий полігонометричний хід, прокладений між відомими точками А та В.

Але координати усіх точок ходу, зокрема точки В, обчислювались не за зрівноваженими, а за виміряними лініями і кутами, починаючи від точки А . У результаті кінцева точка ходу зайняла положення В'. Отже, відрізок В'В = f_s -це лінійна нев'язка ходу. З'єднаємо точки А та В' прямою (замикаючою) і

286

Планові геодезичні мережі

дещо продовжимо її. Дирекційний кут замикаючої а. Дирекційний кут нев'язки є. Довжина замикаючої АВ' =L. Спроектуємо точку В на коорди­натні осі X та 7 і на замикаючу. Отримаємо точки В_х, В₂,В₃.

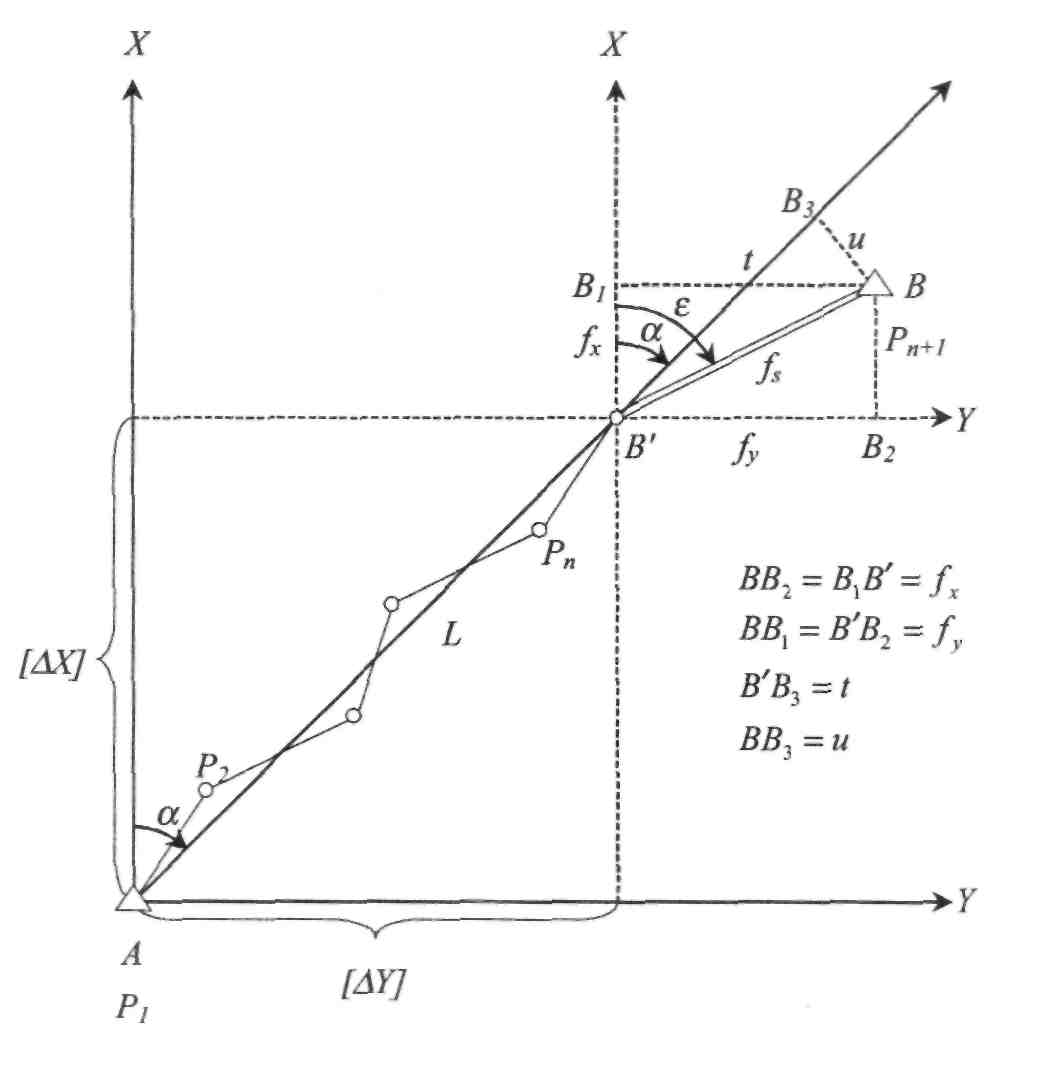
Рис. 11.8.2. До виведення залежності між зсувами t і и та нев'язками по осях координат f_x та f

Як видно з рисунка, відрізки: В'В_Х= ВВ₂ =f_x\ В'В_г = ВВ_Х -f_y- Ці відрізки дорівнюють нев'язкам /_х та f . Відрізок В'В₃ = t - поздовжній зсув; а ВВ_г = и- поперечний зсув. Проектуючи хід на осі X та Y , одержимо суми приростів координат [Аг] та [Ау].

(ІІ.8.9)

Безпосередньо з рисунка маємо:

(II. 8.10)

З рисунка також можемо записати:

287

Розділ II

Розкладаючи cos (є - а) та sin (є - а), отримаємо:

(II. 8.11) (П.8.12)

Враховуючи (II.8.10), маємо:

(ІІ.8.13)

(П.8.14)

Оскільки з цього самого рисунка

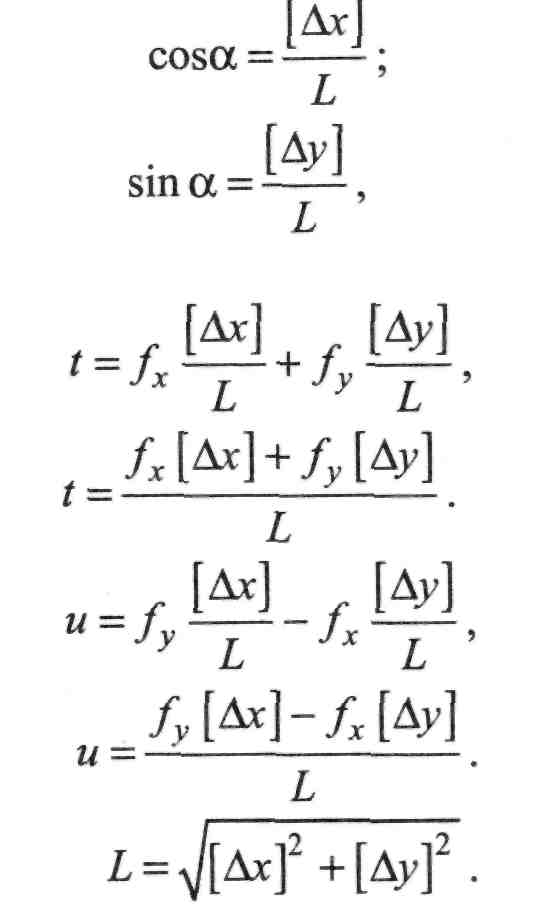
(ІІ.8.15)

(ІІ.8.16)

то

(ІІ.8.17)

(И.8.18)

(П.8.19)

Формули (II.8.17), (ІІ.8.18) пов'язують зсуви ходу t, u з нев'язками по осях координат f_x,f_y.

11.8.4. Виведення умовних рівнянь, що виникають у полігонометричному ході, прокладеному між відомими пунктами

Скористаємось розглянутими в п. II. 8.1 відомими вимогами рівності суми поправок у кути та у прирости координат відповідним нев'язкам, взятим з оберненим знаком.

Ці рівності запишемо так:

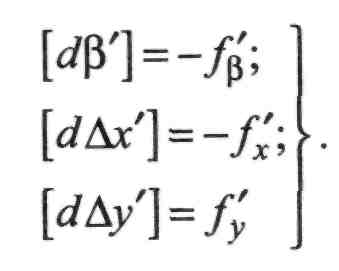
288

Планові геодезичні мережі

Припустимо, що ми нев'язку /о' порівну розподілили в усі виміряні кути.

Нехай виникла необхідність у виправлені кути ввести ще якісь вторинні поправки. Тоді сума цих поправок повинна дорівнювати нулеві. У про­тилежному випадку в ході з'явиться нова нев'язка. Але, якщо ми замінили виміряні кути Р; первинними поправками, то зміняться і дирекційні кути, а, отже, зміняться нев'язки f'_x та f' Одночасно виникне необхідність змінити

поправки у прирости абсцис і ординат.

У зв'язку з цим рівняння (ІІ.8.20) змінюються, і їх запишемо так:

Як відомо, прирости абсцис та ординат знаходять за формулами

(П.8.21)

Продиференціюємо ці формули:

(П.8.22)

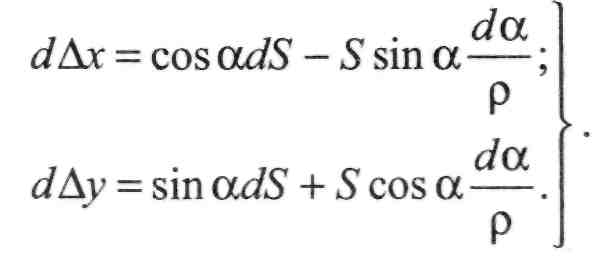
(ІІ.8.23)

Значення dAx та dAy із рівнянь (ІІ.8.23) підставимо у початкові рівняння (П.8.21), враховуючи (П.8.22). Отримаємо:

(II. 8.24)

Перейдемо від поправок у дирекційні кути da_t до поправок у виміряні кути с/р,. Для цього скористаємося залежністю між дирекційними кутами та кутами повороту. Припустимо, вимірялись ліві по ходу кути. Тоді можемо записати:

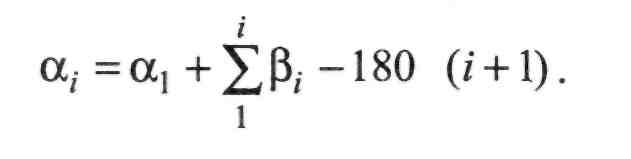
(ІІ.8.25)

289

Розділ II

Диференціюючи формулу (ІІ.8.25) за змінними кутами, одержимо:

1 Підставимо значення da_t з (ІІ.8.26) у (ІІ.8.24). Отримаємо:

(ІІ.8.26)

Позначимо

Запишемо суму А у розгорнутому вигляді:

(II. 8.27)

(ІІ.8.28)

Замінимо суми приростів ординат різницями координат відповідних

точок:

В останній сумі відсутній кут р„₊₁ і поправка ар„_н. Введемо цю поп­равку, скориставшись виразом, що дорівнює нулеві: d$_n+l (у_п+\ - у„₊\) ■ Цей ви­раз додамо до А. Тоді останній вираз можемо записати скорочено:

(ІІ.8.29) Введемо в рівняння (П.8.29) ординату центра ваги ходу:

(ІІ.8.30)

290

Планові геодезичні мережі

Це можна зробити, враховуючи, що [с/р,] = 0. Отже, (П.8.29) можна за­писати так:

(ІІ.8.31) (П.8.32)

(ІІ.8.33) (ІІ.8.34)

Позначивши в (II..31) різниці

де - ординати точок ходу відносно центра ваги ходу. Матимемо:

Позначивши

де - абсциси точок ходу відносно центра ваги, можемо за аналогією записати:

(П.8.35) Отже, умовні рівняння набувають вигляду:

(И.8.36)

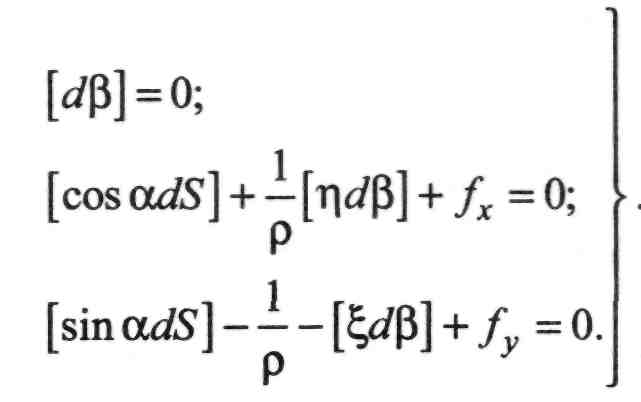
Оскільки у рівняннях (П.8.36) поправки в кути с/р та в лінії dS записані двома літерами, доцільно ввести позначення: d$ = V; dS = CO, тобто позначити однією літерою поправки в кути V, а поправки в лінії со. Тоді записи (П.8.36) спростяться:

Це і є умовні рівняння в кінцевому вигляді.

(ІІ.8.37)

291

Розділ II

Зауважимо, що, як це буде очевидно з подальшого тексту, введення центральних координат спрощує обчислення під час зрівноваження ходу.

Необхідно, однак, для повнішого розуміння суті справи подати гео­метричну інтерпретацію координат центра ваги ходу Х_ц, У_ц та координат

точок ходу відносно центра ваги

Рис. 11.8.3. Геометрична інтерпретація координат центра вагиХ , Y та координат відносно центра ваги

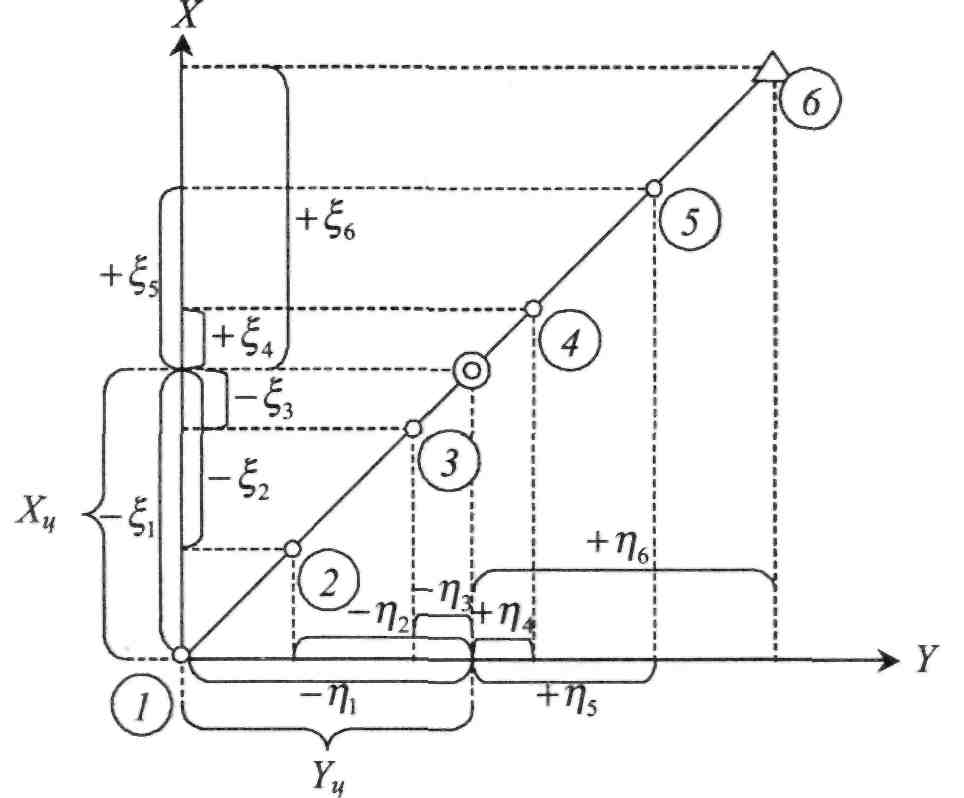
Для простоти скористаємось витягнутим рівностороннім полігономет-ричним ходом із шести точок, п'яти сторін, показаного на рис. ІІ.8.3:

292

Планові геодезичні мережі

З рисунка, наприклад, очевидно, що в ході три ординати rjj, r\₂, Лз точок 1,2,3 від'ємні, а три гц, т\₅, Ц₆ точок 4, 5, 6 - додатні. До того ж зрозуміло, що сума [її, ] = 0. Аналогічно, сума [^ ] = 0.

11.8.5. Строге зрівноваження довільного полігонометричного ходу

корелатним методом

Розглянемо послідовність і суть методу. Нехай для довільного ходу маємо систему умовних рівнянь:

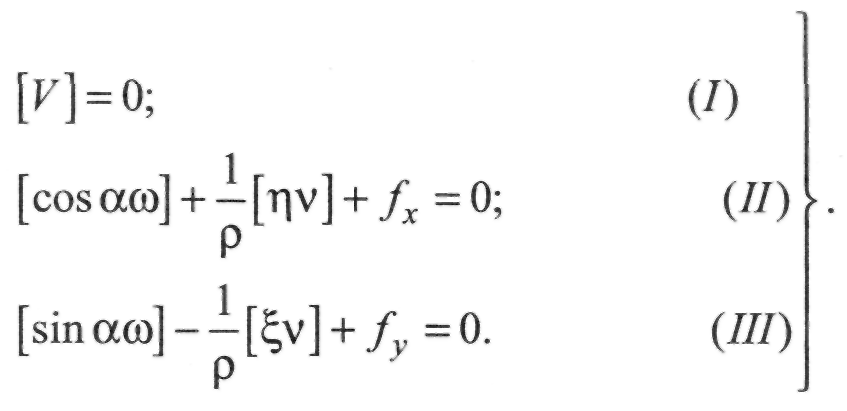(ІІ.8.38)

Будемо одночасно розв'язувати ці рівняння під додатковою умовою:

де — ваги вимірювання ліній; — ваги вимірювання кутів.

Як відомо, ваги вимірювання - величини, обернено пропорційні до квадратів квадратичних похибок. Тому запишемо:

де - коефіцієнт випадкового впливу лінійних вимірів; щ- похибка

вимірювання кута; с - довільний коефіцієнт пропорційності.

Користуючись довільністю с , приймемо: с =\і . Тоді отримаємо:

Отже, ваги виміру ліній - змінні величини й обернено пропорційні до довжини ліній, а кути мають однакові ваги, оскільки вимірюються приладами однієї точності і за однаковою програмою вимірювань.

293

Розділ II

Як відомо зі способу найменших квадратів, розв'язання (ІІ.8.37) під додатковою умовою (II.8.38) приводить до нормальних рівнянь корелат, яких буде стільки, скільки умовних рівнянь. У загальному вигляді нормальні рів­няння корелат записуються так:

(ІІ.8.39)

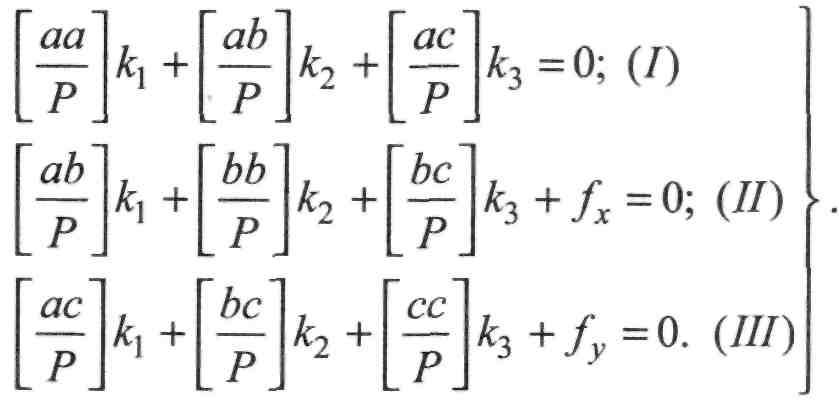
У цих рівняннях к_х, к₂, к₃ - корелати - проміжні невідомі, знайшовши які, надалі можна буде обчислити шукані поправки у кути V, і в ліній ю₍.

Літерами a_t, Ь_і, с_і позначено коефіцієнти при невідомих поправках у кути та лінії відповідно в умовних рівняннях І, II, Ш системи (ІІ.8.37).

Складемо таблицю коефіцієнтів відповідно до (И.8.37) окремо для поправок у кути та в лінії.

Таблиця II. 8.1