11.3.12. Похибка редукції

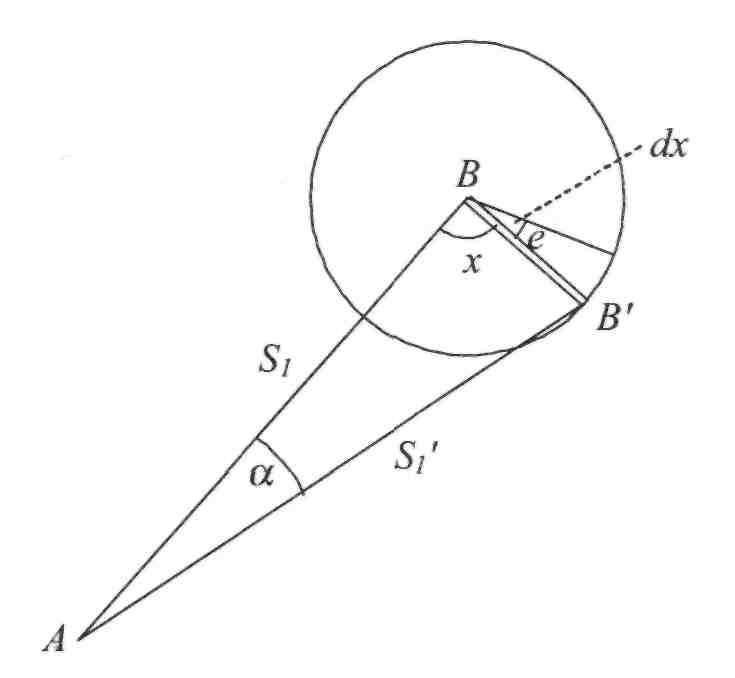
Припустимо, що у напрямку АВ (рис. ІІ.3.22) візирна марка встановлена не в точці В (не над центром геодезичного знака), а помилково в точці В'. Лінійна величина редукції - є . Кутова похибка редукції - малий кут а. Сторони S_l та S{ трикутника ABB' практично рівні. З цього трикутника, ос­кільки кут а малий, можемо записати:

(П.3.47)

Точка В', рухаючись по колу радіуса є, може займати різні положення. Кут х буде змінюватися разом з кутом а". Для х = 0° та х = 180°, а' = 0. Для

195

Розділ II

х = 90° та х = 270° а" набуває максимального значення. Нехай точка переміщається з постійними кутами dx; тоді п - кількість положень точки В' знайдемо за такою формулою:

2л

(П.3.48)

Рис. 11.3.22. Редукція одного напрямку

Кожному положенню точки В' буде відповідати похибка редукції в деякому напрямку і.

Квадрат середньої квадратичної похибки редукції в напрямку /' ста­новитиме:

р'²е² sin² х

(ІІ.3.49)

або

(П.3.50)

Можна довести, що інтеграл J sin xdx = n. Тому формула (П.3.50) набу-

о де вигляду:

(ІІ.3.51)

196

Планові геодезичні мережі

Для другого напрямку кута з вершиною в точці А (для довжини S^) похибка:

(П.3.52)

Сумарна квадратична похибка редукції:

(ІІ.3.53)

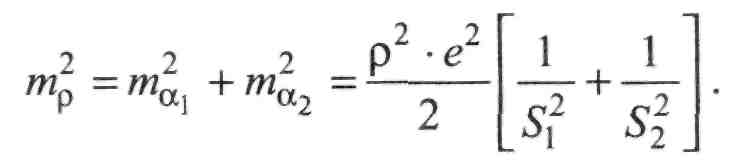
Для S, =S₂=S матимемо:

(ІІ.3.54)

Як бачимо з (II.3.54), похибка редукції прямо пропорційна до лінійної редукції і обернено пропорційна до довжини ліній S, що створюють кут.

Для є = 10 мм та за мінімальної допустимої довжини сторони ходу

'; таке значення

.... _ ._- , 0,01м-206265' полігонометрії 4 класу S = 250 м, т_р =

недопустиме. За нашими розрахунками за (ІІ.3.41) допустиме значення окремого джерела кутової похибки (у такому випадку похибка редукції) т" =

2,4". Знайдемо допустиму лінійну похибку центрування візирної марки, розв'язавши формулу (II.3.54) відносно є :

(ІІ.3.55)

Мінімальна сторона S полігонометрії 4 класу за інструкцією [5] стано­вить 250 м. Тоді:

Оптимальна довжина сторони ходу S = 500 м. е_доп= 5,8 ~ 6 мм. На підставі розрахунків можна зробити два висновки:

1. Для коротких сторін центрування марки необхідно виконувати значно точніше ніж для довгих сторін.

2. Забезпечити точність центрування марки, встановленої на штативі, З мм нитковим виском - важко. Необхідно застосовувати оптичний висок.

197

Розділ II

11.3.13. Похибки центрування теодоліта

Припустимо, що під час вимірювання кута теодоліт встановлено поза центром знака, тобто в точці А, а не в точці D. Тоді буде виміряний кут А, а не кут D (рис. П.3.23). Нехай точка А переміщається по колу радіуса є . Звернемо увагу на те, що на відміну від впливу редукції, вплив центрування теодоліта завжди впливає на кут, що вимірюється, де б не була розміщена на колі точка А.

Рис. 11.3.23. Встановлення теодоліта поза центром

Розглянемо трикутник АМВ та DMC. Кути в точці М в них однакові. Тому кути

(П.3.56) або

(П.3.57) З трикутника ABD знайдемо:

(П.3.58)

є $[ '

Оскільки кут а малий і S[ ~ &, тоді запишемо:

sin a sin х

(ІІ.3.59)

Своєю чергою, з трикутника ACD знаходимо:

eVsin(x + D)

(П.3.60)

198

Планові геодезичні мережі

Якщо точка А також переміщається по колу радіуса є з інтервалами ск, то кількість встановлень теодоліта становитиме тому для кожного

положення точки А, враховуючи (П.3.57), можемо записати:

т¹_ц=т^г=т²_а+т\. (П.3.61)

За аналогією з похибкою редукції запишемо в розгорнутому вигляді:

dx. (П.3.62)

sin'

Після інтегрування та деяких перетворень матимемо:

(П.3.63)

де с - віддаль між точками А та С (див. рис. П.3.23).

Для гострих кутів A =D, значення с мале. Для витягнутого ходу

А = D = \S0°,c = S_l+S₂. Якщо^ =S₂=S, тоді с = 2S, ac²=4-S². У такому разі (П.3.63) набуде вигляду:

(П.3.64)

або

(ІІ.3.65)

Порівнюючи формули (ІІ.3.54) та (П.3.65), бачимо, що вплив похибок центрування на виміряний кут в більший, ніж вплив редукції візирних

цілей. Поставимо вимогу, щоб т_ц = т , тобто:

Отже, є , або

є =-?=. (П.3.66)

V2

Якщо є відповідно 3 мм і 6 мм, тоді є = 2 мм, є'-4 мм.

Отже: 1) теодоліт необхідно центрувати точніше ніж візирні марки; 2) обов'язково використовувати оптичні виски або якісь інші методи знешкод­ження впливу похибок центрування на кутові вимірювання.

199

Розділ II

11.3.14. Методи зменшення похибок редукції та центрування

Розглянемо спочатку можливі методи зменшення похибок редукції. На­гадаємо, що під час вимірювання горизонтальних кутів у теодолітних ходах як візирні цілі зазвичай використовують віхи. Інколи, щоб не тримати віху в руках вістрям над центром знака, робітник встромляє віху в землю поруч з центром знака. У полігонометрії це недопустимо. Тому:

1. Використовують віхотримачі. Це металеве кільце, до якого шарнірно прикріплені металеві стрижні - ніжки віхотримача (рис. П.3.24). Віху встановлюють в кільце, ставлять вертикально так, щоб вістря віхи було над центром знака. Вертикальність віхи перевіряють за допомогою виска на нитці. Корегуючи розташування верху віхи, ніжки віхотримача встромляють в землю на різні глибини.

Рис. 11.3.24. Віхотримач Рис. 11.3.25. Види оптичних центрирів

2. Віхи (для коротких ліній) заміняють шпильками; головне призначення шпильок - фіксувати кінці вимірювальної стрічки для лінійних вимірювань.

3. Шпильку можна замінити звичайним стрижнем.

4. Застосування оптичних центрирів (рис. ІІ.3.25).

Способи підвищення точності центрування теодоліта

1. Важкий висок. Нитка такого виска менше відхилятиметься вітром від вертикального стану.

2. Жорсткий висок. Це висок не на нитці, а на тонкій металевій штанзі із загостреним кінцем. Довжину штанги можна змінювати. Така штанга, прикріплена шарніром до станового гвинта, під своєю вагою займає вер­тикальне положення.

200

Планові геодезичні мережі

3. Оптичний центрир теодоліта.

4. Лазерний центрир. Дуже зручний.

Проте найефективнішим способом, яким практично повністю можна знешкодити як вплив редукції, так і центрування, є так звана триштативна система. Основою такої системи є три універсальні підставки теодоліта. Універсальність підставок полягає в тому, що на них можна встановлювати не тільки теодоліт, але й візирну марку, знявши теодоліт з підставки. Вертикальна вісь обертання теодоліта на підставці повинна збігатися з вертикальною віссю марки. У підставки вмонтовують оптичні виски. На рис. П.3.26 підставки показано трикутниками, кружками показані місця, в які вставляють теодоліт або візирну марку, крапками - точки, через які проходить вертикальна вісь теодоліта або марки.

Встановлену на штатив підставку з оптичним центриром центрують над центром геодезичного знака і її розташування не змінюють, на підставку встановлюють теодоліт, знявши оптичний центр, або, знявши теодоліт, встановлюють візирну марку. Штатив та підставку залишають в незмінному стані. Наприклад, вимірюють кут (3₂ на точці 2, а на точках 1 та 3 встановлено візирні марки. Теодоліт та марки попередньо встановлені за допомогою оптичних центрирів. Після вимірювань теодоліт (без підставки) знімають з точки 2 і на цю підставку, що залишилася на штативі, встановлюють задню візирну марку. Теодоліт переносять на точку 3, знімають передню марку (без підставки). Теодоліт встановлюють точно над тією самою точкою, над якою тільки що була встановлена передня візирна марка. Передню візирну марку встановлюють над точкою 4. Використовують штатив (що' звільнився), на якому була встановлена задня візирна марка (можна мати ще один штатив). Потім вимірюють кут Р₃ і так далі. Теодоліт та візирні марки ніби "відри­ваються" від центрів знаків, розташованих на земній поверхні, і створюється (якщо полігонометричний хід замкнутий) багатокутник у "повітрі" (фактично в точках, де встановлюють теодоліт та марки). Саме в цьому "повітряному

201

Розділ II

багатокутнику" виконують вимірювання кутів, і на значення кутів практично не впливають ні похибки центрування, ні редукції. Кутові нев'язки, викликані цими факторами, виключаються, хоча зрозуміло, що діяли похибки центрування підставок оптичними висками.

11.3.15. Похибки вимірювання горизонтальних кутів

Як ми вже знаємо, до цих похибок належать похибки наведення труби на візирну ціль та похибки відліків лімба (горизонтального кута). Розглянемо окремо, як впливають ці похибки на вимірювання кутів методом кругових прийомів та методом повторень, якщо кут виміряний одним повним прийомом або одним повторенням, а також якщо кут виміряний п прийомами або Р повтореннями.

Спосіб кругових прийомів

Нехай вимірюють кут (3, утворений двома напрямками (див. рис. И.3.27). Як відомо, під час вимірювання, після наведення труби на ціль беруть два відліки і з них виводять середнє значення.

^т,

■п

^тв

4і

Рис. 11.3.27. До розрахунку похибок вимірювання горизонтального кута методом кругових прийомів

Нехай труба наведена на ліву ціль та взято відлік . Похибка відліку т_в, похибка середнього відліку, якщо діють тільки випадкові похибки, ста­новитиме —j=; випадкову похибку наведення труби позначимо т_н.

л/2

Аналогічно, під час наведення труби на праву ціль взято відлік в; найімовірніші похибки також . Оскільки поділки на лімбі зростають

за ходом годинникової стрілки, то кут Р знайдемо з виразу

p = e-a. (II.3.67)

202

Планові геодезичні мережі

З виразу (ІІ.3.67), що є різницею двох змінних величин, можемо (на основі теорії похибок вимірювань) записати для півприйому (при КЛ або КП) квадрат середньої квадратичної похибки:

або

(П.3.68) (ІІ.3.69)

Квадрат похибки одного прийому становитиме:

(П.3.70)

або

(П.3.71)

Квадрат похибки кута, виміряного п прийомами, становитиме:

(ІІ.3.72)

Отже,

(П.3.73)

Спосіб повторень Як і раніше, нехай кут Р виміряний методом повторень. Наводимо трубу на

• • ^тв

ліву ціль. Беремо два відлжи. Будемо мати похибки середнього відліку —= та

V2 наведення т_н . Далі наведемо трубу на праву ціль. Відлік не беремо. Буде тільки похибка наведення т_н . Потім здійснюємо тільки наведення труби р разів, на лівий і на правий предмети. Кінцеве наведення труби на праву ціль. Беруть два

ТП

кінцеві відліки. Похибка середнього з них —j=. Квадрат похибки Р кратного кута

V2

Р, виміряного за одного розташування вертикального круга, становитиме:

або

(П.3.74) (П.3.75)

203

Розділ II

Рис. 11.3.28. До розрахунку похибок вимірювання горизонтального кута способом повторень

Квадрат похибки Р -кратного кута, виміряного за двох розташувань вертикального круга, становитиме:

Допустимо, однократний кут (3, а Р -кратний кут -А . Тоді:

(ІІ.3.76)

(ІІ.3.77) Це найпростіша функція добутку постійної величини 1/Р на змінну Л.

7 9

Оскільки т_А = та , тоді

Тому:

Вираз (П.3.79) можна ще записати так:

(П.3.78)

(П.3.79)

або

(ІІ.3.80)

Щ

J\

ті + "

2Р

(П.3.81)

Порівнюючи формули (ІІ.3.73) та (П.3.81), зауважимо, що коли п = Р (кількість прийомів дорівнює кількості повторень), похибка відліку під час

204

Планові геодезичні мережі

вимірювання методом повторень в Р разів менша за похибку відліку, ніж під час вимірювання способом кругових прийомів. Саме через це спосіб повторень був основним способом вимірювання кутів, коли не було високоточних відлікових пристроїв. Сьогодні спосіб втратив колишню популярність.